| 3 接ベクトル空間 | ||
| f-denshi.com [目次へ] 最終更新日:22/04/10 | ||
| サイト検索 | ||
[1]
| 定義 Cs級の曲線
区間 (−ε,ε) ∈R から Cr級 m次元多様体 M への Cs級写像 c: R → M を Cs級曲線といい,パラメータ t を用いて,c(t) と書く。ただし,0≦ s ≦r ,−ε≦
t ≦ε。 |
特に分かりにくいところはないでしょう。
ここで,m次元 Cr級多様体 M から R への連続写像 f : M → R を考えます。
また,多様体 M上 の点 p を通る Cr級曲線 c(t) は,
−ε≦ t ≦ε , c(tp) = p
を満たすこととします。
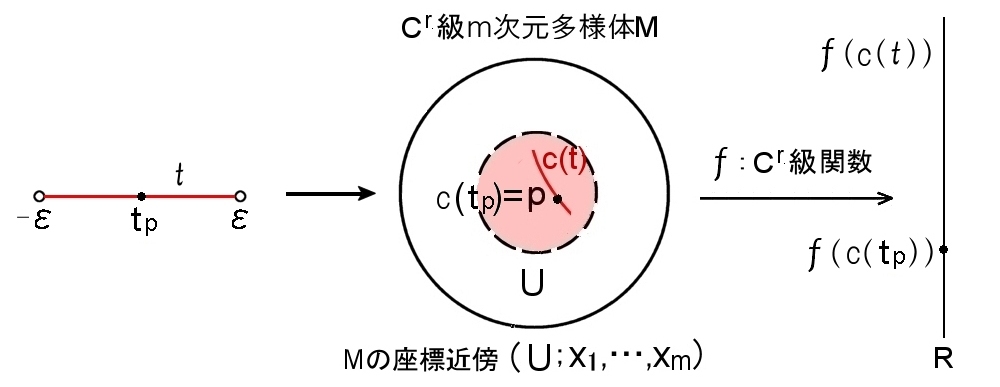
p の開近傍 U で定義された Cr級関数 f : M → R の定義域を曲線 c(t) 上に制限すると,合成関数,
fοc (t) : t → c(t) → f(c(t))
は M ,R の局所座標系に無関係なく, t と曲線 c だけの関数です。
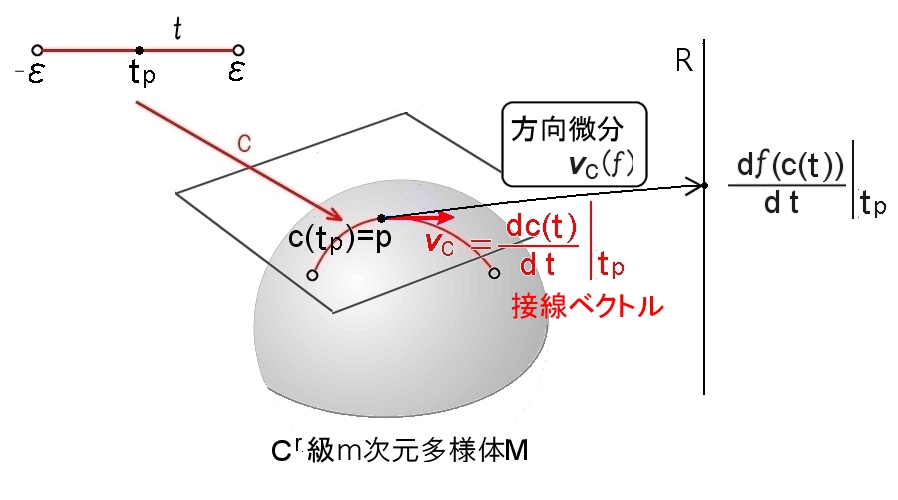
そこで, f(c(t)) の t=tp の微分係数を
df(c(t)) t=tp ≡ df(c(t)) tp ≡ df(c(tp)) d t d t d t
など と書き,(煩雑を避けるときは右端の表記を使う) さらに,f からこの微分係数への対応:
vc : f → df(c(tp)) d t
をvc と書くことにします。
[3] すなわち,f が与えられたら,vc は次の値を返すということです。
vc( f )= d f(c(t)) tp d t
ここで,vc を c に沿う方向微分と呼ぶことにします。(方向微分作用素/演算子とネーミングした方がしっくりくる?)
( vc( f ) は, f の c に沿う方向微分係数 です。すぐ後で証明する)
ここで,強調しておきたいことは,vcは曲線 c(t) と点 p∈M に依存するだけであって,これが作用する f とは無関係ということです。
[2] 以上は曲線 c に沿う方向微分ですが,この方向微分のエッセンスを抜き出して,多様体上の点 p における(形式的な)方向微分を次のように定義します。
| 定義 多様体上の方向微分 v ∈ Dpr(M) Cr級m次元多様体 M 上の点 p の開近傍で定義された Cr級関数 f ,g から実数 v(f),v(g) への対応が次の性質をもつとき,この対応を p における方向微分といい,v と表す。 (1) p の十分小さな開近傍で,f=g ならば,v (f)=v (g) (2) v (af+bg)=av (f)+bv (g) a,b ∈R [線形性] (3) v (fg)= v (f) g(p)+f(p)v (g)また,p ∈M における方向微分すべての集合を考えて,それを Dpr(M) と表す。 |
これらはユークリッド空間では微分 (線形作用素,線形演算子) に対して成り立つ命題と呼ぶべきものですが,多様体においては定義として与えることとします。
(この手法は,ユークリッド空間から距離空間,位相空間を定義していくときと同じ流れですね。)
Dpr(M) は,点 p を通るあらゆる曲線に対して定まるv 全体からなる集合と考えることができます。その結果,p だけに依存するDpr(M)が定められたのです。
以上は,局所座標を用いない方向微分とその全体集合の定義です。
このとき,次の命題が成立します。
| 命題:
Cr級多様体 M 上の点 p における, Dpr(M) は R上のベクトル空間となる。 |
ここでのベクトル空間とは線形汎関数 (ベクトルとみなされる関数に働く線形演算子)v のすべての集合からなるベクトル空間です。
関数 f,g など関数の集合が通常の関数の和,実数倍から作られるベクトル空間の元と見なせば,Dpr(M) はそのベクトル空間に対する双対空間 [#] とみなすべきですが,ここでの視点ではベクトル空間とします。
(ベクトルとその双対空間は相対的な関係でしたね。)
[3] 特別な場合として曲線 c が座標曲線 である場合(局所座標が指定されている)を考えてみましょう。
その場合,p∈M における Cr級関数 f の xk方向の偏微分係数への対応を,
∂ p ( f ) ≡ ∂f ( p ) ∈R ・・・・ [*] ∂xk ∂xk
| とすると, | ∂ | p | は方向微分の条件 (定義) [#] を満足している | |||
| ∂xk |
ことは容易に確認できます。すなわち,
v ⇔ ∂ p ∈ Dpr(M) ∂xk
ということです。
[4] m個の座標曲線が与えられているとします。このとき,
| 命題 Cr級m次元多様体 M 上のDpr(M) に属する m個のベクトル,
は1次独立である。 |
証明は,任意の f について,
a1 ∂ p +a2 ∂ p …+am ∂ p =0 ∂x1 ∂x2 ∂xm
すなわち,
a1 ∂f (p) +a2 ∂f (p) …+am ∂ (p) =0 ∂x1 ∂x2 ∂xm
ならば,a1=・・・=am=0 であることを,多様体上の方向微分の定義 [#] を用いて示せばOKです。(演習)
[4] すると,次のような定義を与えることができます。
| 定義 接ベクトル空間 Tp(M) Dpr(M) に属するm個のベクトル,
で張られるベクトル空間を p における接ベクトル空間 Tp(M) といい,これに属するベクトル,
を接ベクトルという。 |
[4-1] つまり,v には,関数に作用して,その
(1) 方向微分(係数)を与える微分演算子 としての Dpr(M)
(2) 多様体に接する接ベクトル=幾何ベクトルとして Tp(M)
という2つの意味を持っているのです。
証明は省略しますが(教科書「多様体の基礎」参照),C∞級多様体 M の場合は
Dp∞(M) = Tp(M)
となります。しかし, r <∞ の Cr級多様体 では
Dpr(M) ⊇ Tp(M)
となります。
この講義では,Dp∞(M) = Tp(M)の場合やそのような部分空間しか考えないので,この2つを混同しても構いません。
| 定義 速度ベクトル
c : (-ε,ε) → M が Cr級曲線で,c(tp)=p を満たすとき, で定義される [#] 接ベクトルvc ∈Tp(M) を曲線c の t=tp における速度ベクトルという。 |
≡ の右の表記の妥当性は,Mの局所座標 (x1,x2,…,xm) が与えられて,
c(t) = x1(t) x2(t) : xm(t)
とすれば,
vc( f )= df(c(t)) tp = df((x1(t),x2(t),…xm(t)) tp d t dt
= dxk (tp) ∂f ( p ) dt ∂xk
↓ ∂ p ( f )= ∂f ( p ) [*] より ∂xk ∂xk
= dxk (tp) ∂ p ( f ) dt ∂xk
よって,最初と最後の式を比較して,
vc = dxk (tp) ∂ p ・・・・ [***] dt ∂xk
と表してもよいことが分かります。
| よって,vc は基底 | ∂ | p | (k=1,2,…,m) で展開できて,vc ∈Tp(M)。 | ||
| ∂xk |
また,この基底による成分表示は,縦ベクトルとして,(横ベクトルでも構わないのですが,この講義では縦に統一します。)
vc =
∂x1 (tp) ∂t
:
:
∂xm (tp) ∂t
と書くことができ,これは曲線 c のp における
| 接線ベクトル | dc(t) | に他なりません。 | ||
| dt |
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[6] まとめておきます。
| 命題 区間 (−ε,ε) ∈R から Cr級多様体 M 上の Cs級曲線 c の局所座標表示, を用いると,速度ベクトルは, と書くことができる。最後の縦ベクトルの基底は,
|
当然ですが,速度ベクトルそのものは局所座標系に依存しません。
しかし,基底は座標系ごとに定まる(異なる)ために,その基底に対応した速度ベクトルの成分表示は座標に依存することになります。
初等的な線形代数 [#] ,ベクトル解析 [#] のベクトル表記と比較すると次のようになります。
vc= dxk (tp) ・ ∂ p ⇔ xk ・ ek dt ∂xk 成分 基底 成分 基底
このアナロジーは今後,多様体上の多くの概念を掴むのに役立つはずです。
[7] 特別な場合として曲線 c が s 番目の座標曲線と一致する場合を考えてみましょう。つまり,曲線c として,
cs(t)=(a1,a2,…,as+t,…,am), a1,…am は定数
を考えます。すると,
dxs (tp) =1, dxk (tp) =0 (k≠sのとき) dt dt
であるから,
vcs= ∂ p = ∂xs 0 ←s番目の成分 : 1
:0
となります。つまり,c が 一つの座標曲線であるときは,
「 速度ベクトルは,座標曲線に接する基底ベクトル 」
となっており, Rm の場合は任意の点 p ∈Rm で,
∂ p , ∂ p ,… , ∂ p ∂x1 ∂x2 ∂xm
は定ベクトルで標準基底,e1,e2,…,em [#] と一致します。
ここまで述べてきたこととは逆の方向で考えることもできます。
| 命題
任意の接ベクトルv に対して,ある曲線 c(t) が存在して,その速度ベクトルc' (t) が接ベクトルと一致する。 |
この証明を含む内容のことは次のページで説明します。
[8] 引き続き,曲線 c が座標曲線である場合を考えます。p∈M の周りで2つの座標近傍 (Ux,x1,x2,…,xm),(Uy,y1,y2,…,ym) が存在して,Ux∩Uy≠φであるならば,接線ベクトル空間 Tp(M) はどちらの座標近傍に基づく基底を用いても記述することができます。このとき,
| 公式 基底変換
p∈M の周りの2つの座標近傍 (Ux,x1,x2,…,xm),(Uy,y1,y2,…,ym) に対応する Tp(M) の2組の基底,
の間には次の関係式が成り立つ。
|
この関係式は基底変換に対応しており,物理学では共変(的)変換ということもあります。
線形代数で示した基底変換の公式 [#] と比較するとると解りやすいしょう。
ej = ∂x’k e’k ( = qkje’k )
∂xj
=
∂x'1 ∂xj
← 対応する基底は上から,
e’1,e’2,…,e’m:
:
∂x'm ∂xj
ここでの基底変換とは,次のように対応しています。
yk ⇔ x'k , および,ej ⇔ ∂ p , e’k ⇔ ∂ ∂xj ∂yk
[9]
証明
2つのCr級座標近傍を ((Ux,x1,x2,…,xm),((Uy,y1,y2,…,ym) として,Ux∩Uy (≠φ) における座標変換の式を,
y1 = y1(x1,x2,…,xm)
y2 = y2(x1,x2,…,xm)
…
ym = ym (x1,x2,…,xm)
とするとき,M上の任意の (合成) 関数 f について成り立つチェーンルール[#] を p ∈Ux∩Uy (≠φ) の点で, ( p の関数であることを強調して )
∂f (p) = ∂yk (p) ∂f (p) ∂xj ∂xj ∂yk
と書くことにする。方向微分の記号 [#] で表すと,
∂ p (f)= ∂yk (p) ∂ p (f) ∂xj ∂xj ∂yk
これは任意の f について成り立つので,
∂ p = ∂yk (p) ∂ p ∂xj ∂xj ∂yk
が成り立つことが分かります。
x,y について対称的なので,これらを交換した次式も成り立ちます。
∂ p = ∂xk ,(p) ∂ p ∂yj ∂yj ∂xk
[10] 基底変換に対応して,座標成分も変換されるわけですが,
そのことについてはベクトル場のところを見てください。 ⇒ [#]
(p の添え字のあるなしの違いだけです。)