| 7-1 押し出し・引き戻し | ||
| f-denshi.com [目次へ] 最終更新日:22/05/10 校正中 | ||
| サイト検索 | ||
[1] 同次元の多様体 M から N への C∞級微分同相写像をφとし,M上のベクトル場を X とする。このとき,
(φ*X)φ(p) ≡ (dφ)p(Xp) =Xφ(p) (=Xq) (∀p∈M) ・・・(1)
によって定義されるN上のベクトル場を X の押し出しと呼び,φ*X と表す。
一方,N から R への C∞級関数 f に対して定義される
(φ*f)(p)≡f(φ(p))=fοφ(p) (∀p∈M) ・・・(2)
φ*f ≡ fοφ
を f のφによる引き戻しと呼び,φ*f と表します。ここで,φはMからNへの写像で,引き戻しによって,N上の関数がM上の関数に変換されています。
さらに,Nの1次微分形式ωに対して,Mの1次微分形式,
φ*ω(Xp)≡ωφ(p)( (dφ)p(Xp) )
=(ωφ(p)ο(dφ)p)(Xp) (∀Xp∈TM(M)) ・・・(3)
φ*ω ≡ ωφ(p)ο(dφ)p
をωのφによる引き戻しと呼び,φ*ω ( ={ ωφ(p)ο(dφ)p}p∈M ) と表します。
[2] 多様体上の接空間,余接空間,ベクトル場,微分形式,押し出し,引き戻しを下図にまとめました。
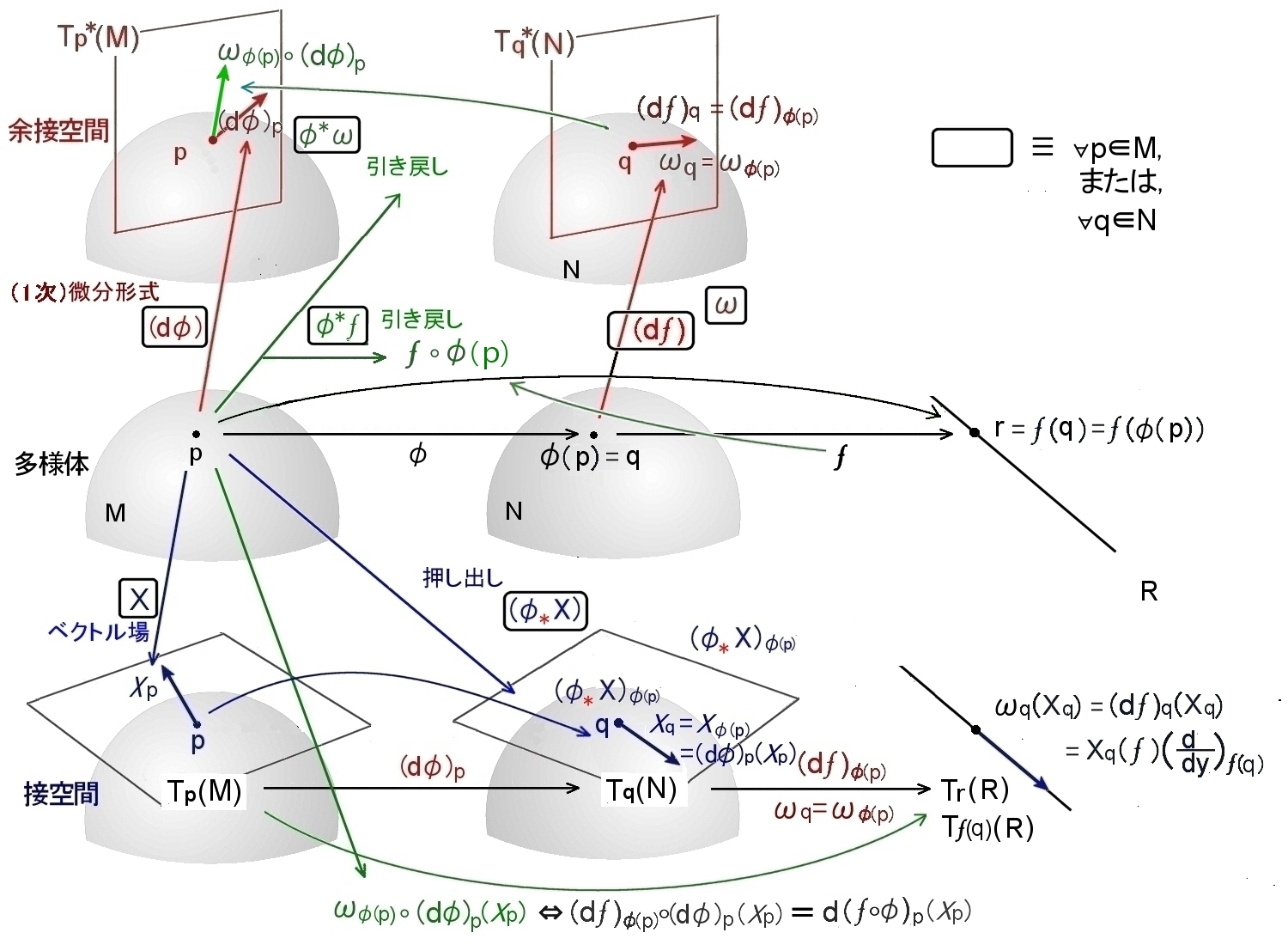
引き戻しφ* は微分同相写像
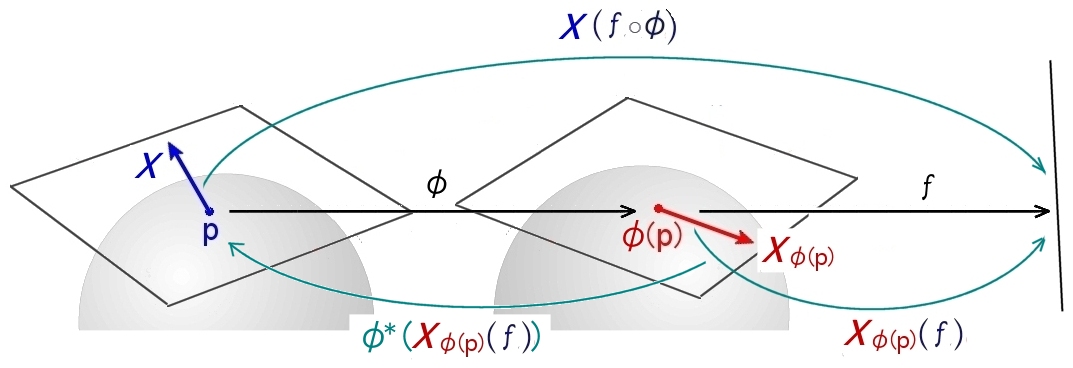
[3] XをM上のベクトル場,φを Mから Nへの写像,f を N上の関数として,
X(φ*f)=φ*((φ*X)(f)) ・・・(4) |
左辺: 関数 f をMに引き戻して Xを作用させる
⇔ 右辺: N へ押し出したX を f 作用させてから,それをMに引き戻す
証明
(Xf)(p)=Xp(f) を用いて,
左辺 (p)=(X(φ*f))(p)
↓ (Xh)(p)=Xp(h) h≡φ*f
=Xp(φ*f)
↓ (2)を用いて(φ*f)=f oφ
=Xp(f oφ)
=(d(f oφ))p(Xp)
=(df)φ(p) o(dφ)p(Xp)
↓ (dφ)p(Xp)=Xφ(p)=Xq ,q=φ(p)
=(df)q(Xq)
=Xq(f)
=((dφ)p(Xp)) (f) ⇔ Xq(f)
↓ (1)押し出しを用いて
=(φ*X)φ(p)(f)
↓ Xp(f)=(Xf)(p) X→(φ*X),p→φ(p)とみなす
=((φ*X)(f)) (φ(p))
↓ 引き戻しを用いて,((φ*X)(f))を(2)の f とみなす
=(φ*((φ*X)(f)))(p)
=右辺 (p)
[4]
|
(1) (ψoφ)*ω = φ*(ψ*ω) (2) φ*( (3) φ*(df) = d(φ*f) |
(3) N上の関数 f の全微分(df) を M上に引き戻す
⇔ N上の関数 f を引き戻し関数の全微分をとる
次ページで述べる外微分と同一視すれば,外微分 d と引き戻し * は可換と考えてもよい。 ⇒ [#]
証明
(1) (3) 繰り返し用いて,
((ψoφ)*ω)(Xp) =(ω(ψοφ)(p)οd(ψοφ)p )(Xp)
=(ω(ψοφ)(p)ο((dψ)φ(p)ο(dφ)p )) (Xp)
=((ω(ψοφ)(p)ο(dψ)φ(p))ο(dφ)p )(Xp)
=(ψ*ω)φ(p)ο(dφ)p (Xp)
=φ*(ψ*ω) (Xp)
(2) fk をC∞級関数,ωをC∞級1次微分形式とすると
φ*(fkωk)(Xp)
↓ 冒頭の(3) 式より
=(fjωj)φ(p) ((dφ)p(Xp))
=fj(φ(p)) (ωj)φ(p) ((dφ)p(Xp))
↓ (2) & (3) より
=(φ*fj)(p) (φ*ωj)(Xp)
(3) (3)より
(df)φ(p)((dφ)p(Xp))=(φ*(df)p)(Xp)
一方,合成写像の微分の公式 [#] を用いて,
(df)φ(p)((dφ)p(Xp))=(d(fοφ))p(Xp)=(d(φ*f)p)(Xp)

[1] 局所座標表示
m次元多様体 M の座標近傍を (U;x1,x2,…,xm),n次元多様体 N の座標近傍を (V;y1,y2,…,yn) とし,M から N への C∞級写像をφ,φ(U)⊂V とします。また,φの局所座標表示が
y1 = φ1(x1,x2,…,xm)
…
yj = φj(x1,x2,…,xm) ・・・・ [*]
…
yn =φn (x1,x2,…,xm)
で与えられるとします。
このとき,N上の1次微分形式の Vの局所座標表示を
ω=fjdyj (5)
ただし,fj = fj(y1,y2,…,yn)
そのM上への引き戻しのUの局所座標表示を
φ*ω=gkdxk (6)
とするとき,fj と gk との関係を求めましょう。
(5) を引き戻すと,公式2-(2)より,
φ*ω=(φ*fj)(φ*(dyj))
ただし,φ*fj = fj(φ1(x1,x2,…,xm),…,φn (x1,x2,…,xm))
ここで,公式2-(3)より,
φ*(dyj)=d(φ*yj)=dφj(x1,x2,…,xm)= ∂φj dxk ∂xk
と書き直せるので,
φ*ω= (φ*fj)(dφj)
= (φ*fj) ∂φj dxk ( = gkdxk )
∂xk
すなわち,
gk= (φ*fj) ∂φj ∂xk
これがN上の1次微分形式 ω=![]() fjdyj をφで引き戻したときの M上の局所座標表示です。
fjdyj をφで引き戻したときの M上の局所座標表示です。
例
n=2,m=3 の場合
ω=f1(y1,y2)dy1+f2(y1,y2)dy2
y1 = φ1(x1,x2,x3) ,y2 = φ2(x1,x2,x3)
をφで引き戻すと,
φ*ω=f1(φ1(x1,x2,x3),φ2(x1,x2,x3)) dφ1(x1,x2,x3)
+f2(φ1(x1,x2,x3),φ2(x1,x2,x3)) dφ2(x1,x2,x3)
=F1 ∂φ1 dx1+ ∂φ1 dx2+ ∂φ1 dx3 ∂x1 ∂x2 ∂x3
+F2 ∂φ2 dx1+ ∂φ2 dx2+ ∂φ2 dx3 ∂x1 ∂x2 ∂x3
= F1 ∂φ1 +F2 ∂φ2 dx1+ F1 ∂φ1 +F2 ∂φ2 dx2 ∂x1 ∂x1 ∂x2 ∂x2
+ F1 ∂φ1 +F2 ∂φ2 dx3 ∂x3 ∂x3
ただし,F1 = f1(φ1(x1,x2,x3),φ2(x1,x2,x3)),F2 = f2(φ1(x1,x2,x3),φ2(x1,x2,x3))
|
定義 k次テンソル場の引き戻し M,N を C∞級多様体,φ:M→N を C∞級写像,ωを N上の C∞級 k次テンソル場とするとき,M上の k次テンソル場 φ*ω, (φ*ω)(X1,…,Xk)=ωφ(p)((dφ)p(X1),(dφ)p(X2),…,(dφ)p(Xk)) ; p∈M をωのφによる引き戻しという。 |
ここで,φの微分は
(dφ)p : Tp(M) →Tφ(p)(N) ( p∈M )
であり, Xj ∈Tp(M) です。
このとき,
(ψoφ)*ω=φ*(ψ*ω)
が成り立つのは1次微分形式のときと同様です。
例 局所座標での計算
n=2,m=3 の場合のN上の2次微分形式,(各局所座標は本文中と同じ)
ω = f12 dy1Λdy2 (8)
ただし,f12 = f12(y1,y2) ;
y1 = φ1(x1,x2,x3) ,y2 = φ2(x1,x2,x3)
とするとき,φによるωのM上への引き戻しは,
φ*ω=f12(φ1(x1,x2,x3),φ2(x1,x2,x3)) dφ1(x1,x2,x3)Λdφ2(x1,x2,x3)
とかける。さらに,
| =F12 | ∂φ1 | dx1+ | ∂φ1 | dx2 | ∂φ1 | dx3 | Λ | ∂φ2 | dx1+ | ∂φ2 | dx2 | ∂φ2 | dx3 | |||||||||||
| ∂x1 | ∂x2 | ∂x3 | ∂x1 | ∂x2 | ∂x3 |
| =F12 | ∂φ1 | ∂φ2 | - | ∂φ1 | ∂φ2 | dx1Λdx2 | |||||||
| ∂x1 | ∂x2 | ∂x2 | ∂x1 |
| +F12 | ∂φ1 | ∂φ2 | - | ∂φ1 | ∂φ2 | dx2Λdx3 | |||||||
| ∂x2 | ∂x3 | ∂x3 | ∂x2 |
| +F12 | ∂φ1 | ∂φ2 | - | ∂φ1 | ∂φ2 | dx1Λdx3 | ||||||||
| ∂x1 | ∂x3 | ∂x3 | ∂x1 |
ただし,F12=φ*f12(y1,y2) = f12(φ1(x1,x2,x3),φ2(x1,x2,x3))
|
公式 M,N をC∞級多様体,φ: M→N を C∞級写像,ω,ηを N上の微分形式とするとき, φ*(ηΛω)=(φ*η)Λ(φ*ω) |
証明 略