| 2 2次元多様体の分類 | ||
| f-denshi.com [目次へ] 最終更新日: 23/08/28 校正中 | ||
| サイト検索 | ||
このページでは2次元多様体の分類を示します。
ほぼ自明と感じるところの証明は省き,とにかくビジュアル重視で,図を上から下へ順にを追っていくだけでも理解できように努めました。
代表的なコンパクトで連結な2次元多様体は,
| 2次元多様体 | 境界 | 向き付け | 構成方法 | |||
| (1) | 円板 D |
1つのS1 | ○ | ■ | ||
| (2) | 球面 S |
なし | ○ | ■+● | ||
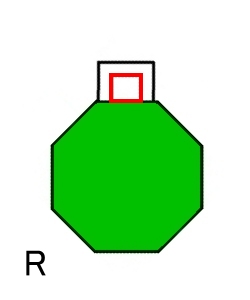
| (3) | アニュラス(円環) R |
2つのS1 | ○ |  |
||
| (4) | メビウスの帯 M |
1つのS1 | 不可能 |  |
||
| (5) | 射影平面 (ボーイ曲面) P2 |
なし | 不可能 |
|
||
| (6) | トーラス面 T2 |
なし | ○ | 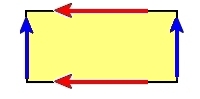 |
||
| (7) | クラインの壷 K |
なし | 不可能 | 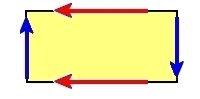 |
ここでは便宜的に,境界を含む2次元円板Δ2 を■で表し,
境界を含まない2次元開円板Δ2−∂Δ2 を●で表わす。
このページでは2次元トーラス面を T2,射影平面を P2 で表す。
正確にはΣ1と書くべきところもS1 (円周と位相同型) を用いています。
であり,2次元多様体はこれらを連結したものになりますが,以下,示すように
最終的には2つの標準系にまとめることができます。
証明が気になる方は,
松本幸夫 著,「4次元のトポロジー」(日本評論社)など
を参考にして下さい。
また,当ホームページ内の「PL多様体の定義」を既読として説明しています。
[1]
(1) 2次元円板Δ2は2次元多様体です。[S0,1]
(2) 2次元球面は2次元円板Δ2と2次元開円板Δ2−∂Δ2の境界S1どおしを張り合わせて (=同一視して )得られる2次元多様体です。[S0,0]
逆に球面から開円板を1つ取り除くと2次元円板に位相同型となります。
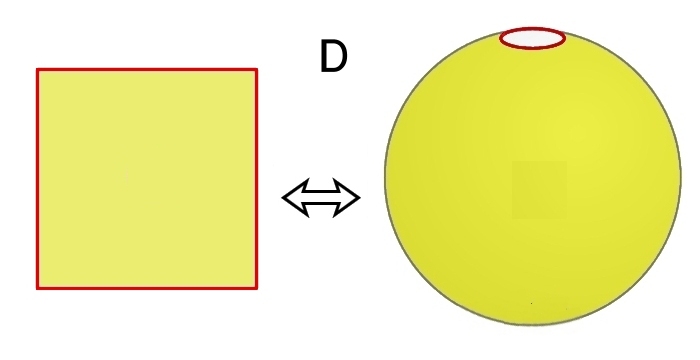
[2]
(3) アニュラス(円環)は四角形の左右の辺を順方向に張り合わせて(同一視して)得られる2次元多様体です。[S0,2]
または,円板から1つの開円板を取り除く,もしくは,球面から2つの開円板を取り除くことでもアニュラスが得られます。
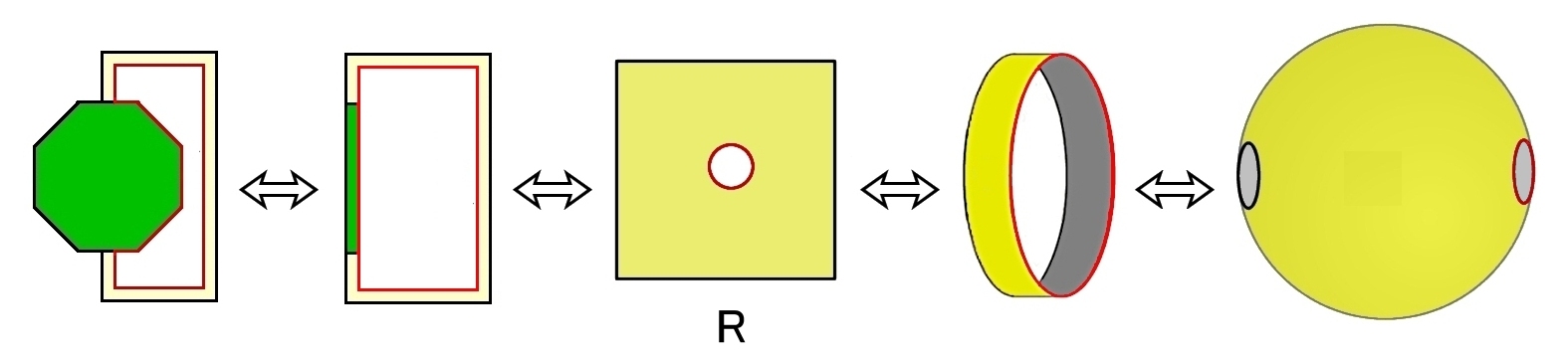 |
| 緑の八角形は後の議論と統一性を持たせるために挿入されている。 |
球面から3つ以上,b個の開円板を取り除いた図形も2次元多様体です。[S0,b]
アニュラスの2つの境界のうちの一つの一部分を,別のアニュラスの一つの境界の一部分と繋ぎ合わせて一つの境界S1とし,合計3つの境界S1をもつ多様体を考えてみましょう。
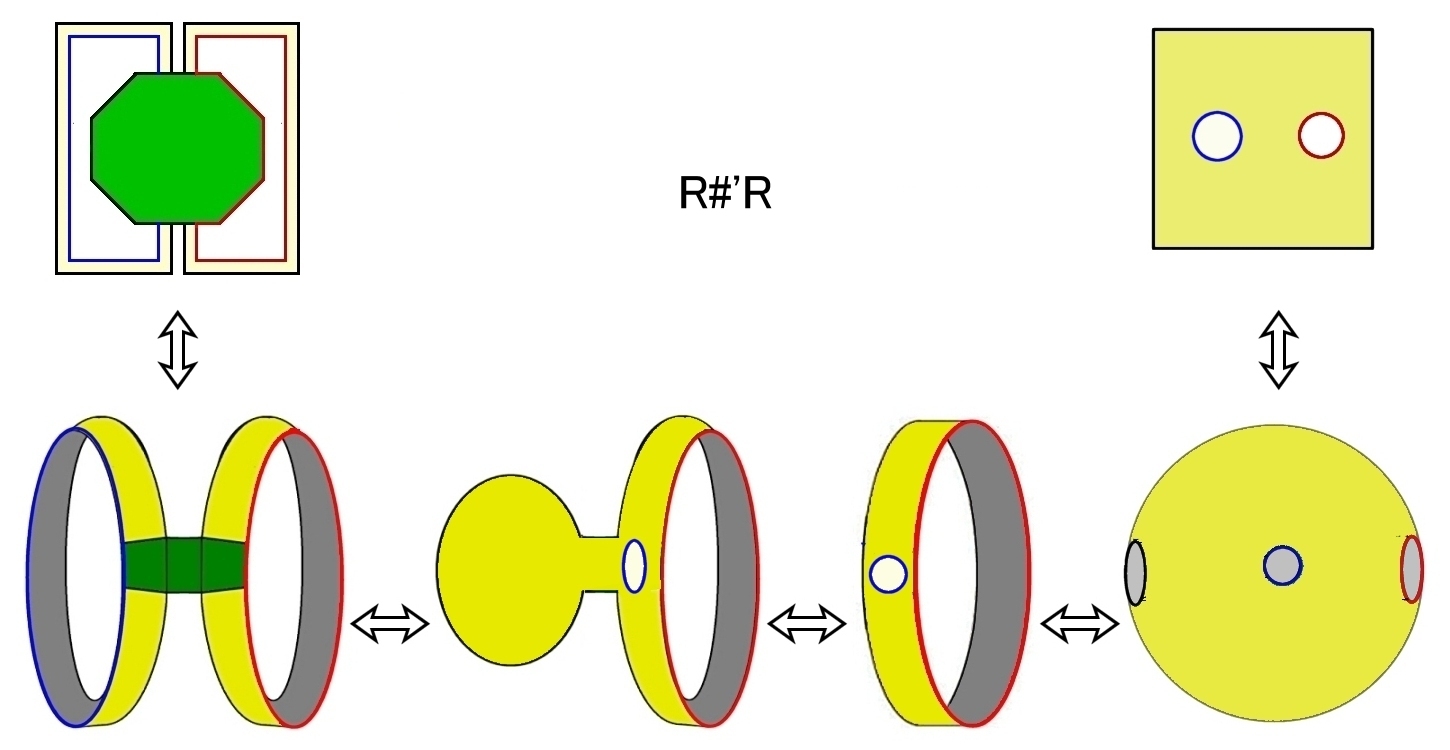
このように2つのアニュラスをつなぐことで得られる2次元多様体 R#'R は,球面から3つの開円板を取り除いた図形 [S0,3] と位相同型です。
ここで,記号 「#'」 は濃緑部分を介して2つの図形を繋ぐ意味に使います。閉多様体の連結和には「#」を用いますが,紛れはないと思います。
通常の連結和を2つのアニュラスに対して行うこともできますが,開円板の穴を双方に開けてその穴を張り合わせます(穴から穴への全単射連続写像を考える)。
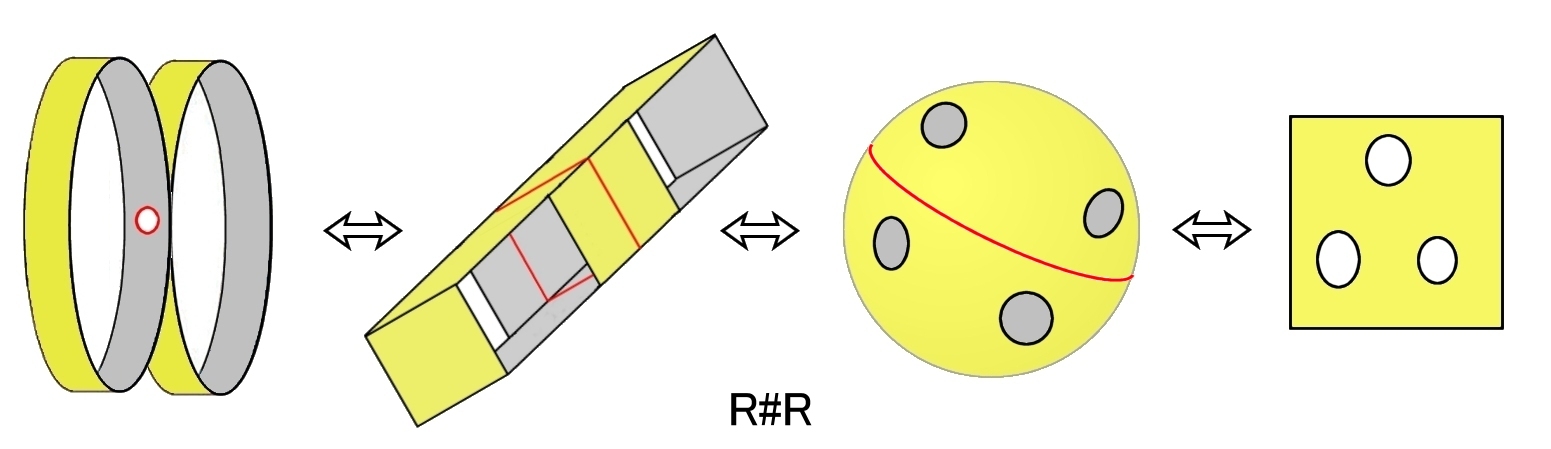
この場合の R#R は球面に4つの穴が開いた球 [S0,4] と位相同型な図形となります。
一方,一つの境界の一部分どおしではなく,境界全体どおしを繋げた場合は2つのトーラスから一つのトーラスができ,新しいタイプの多様体はできません。
[3]
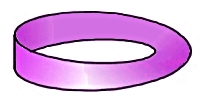
(4) メビウスの帯は四角形の左右の辺を逆方向に張り合わせて(同一視して)得られる2次元多様体です。[N1,1]
 |
⇔ |  |
| ↓ 位相同型 | ||
| メビウス帯 [N1,1] | ||
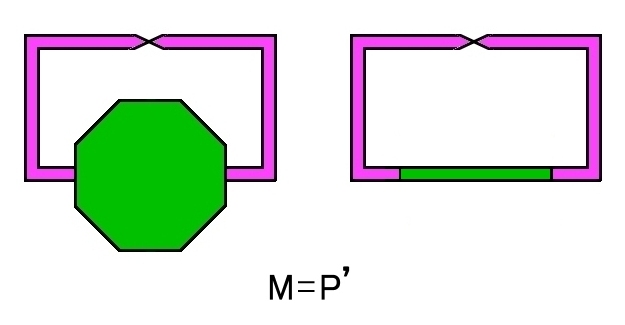
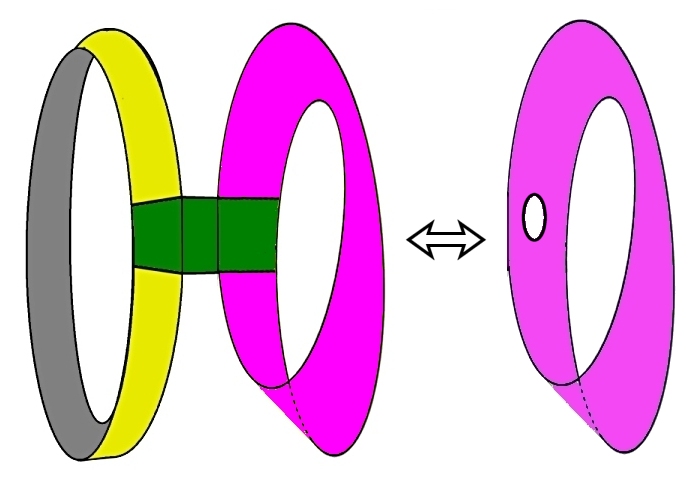
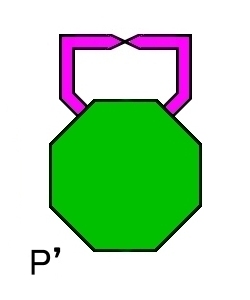
メビウスの帯の境界は一つのS1ですが,これに円板の境界∂Δ2と張り合わせてできる閉多様体は射影平面と呼ばれる図形 [N1,0] です。
逆に射影平面から開円板を取り除いた図形 P’はメビウスの帯 M となります。すなわち,P’=M です。このことについては射影空間 [#] のところで詳述しましたので,まだの方はそれらを参考にしてください。
アニュラスの2つの境界のうちの片方の一部分を,メビウスの帯の境界の一部分と繋ぎ合わせて一つの境界もつ図形は,一つ穴の開いたメビウスの帯となります
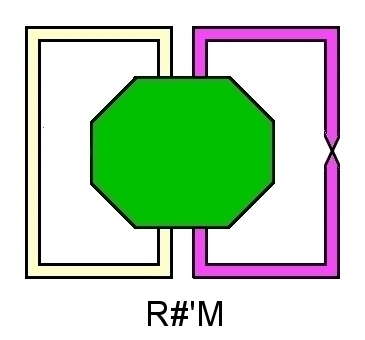 |
⇔ |  |
| R#'M | R#'M = [N1,2] |
このように曲面にアニュラスを「#'」で繋げると曲面に一つ穴ができるとが推測できます。
[4] 位相空間としては,
偶数回の半ひねり=全くひねっていない図形とPL同型(位相同型)
奇数回の半ひねり=1回だけ半ひねりした図形とPL同型(位相同型)
であることは2次元多様体を分類する上で重要な性質です。
したがって,表記上の注意として以下の表現はすべて同じことに注意しましょう。
|
|
| 位相同型な図形の表記の約束 |
[1]
(5) 射影平面はメビウスの帯の境界と2次元開円板の境界を張り合わせて得られる2次元多様体です。[N1,0]
詳細は前のページで説明しています。
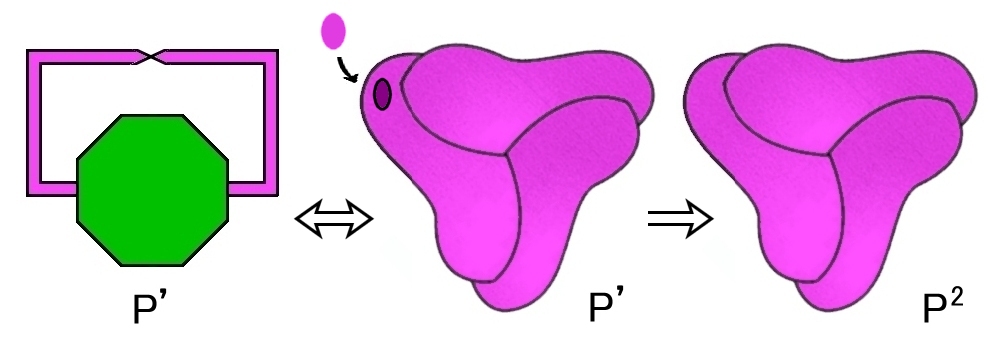
[2]
(6)トーラス面 T2 と(7)クラインの壷 K の説明にはいくつか準備が必要です。
(以下,当ホームページ「PL多様体」を既読として説明しています。)
PLトーラス面を単体分割した下図のような複体を K とします。
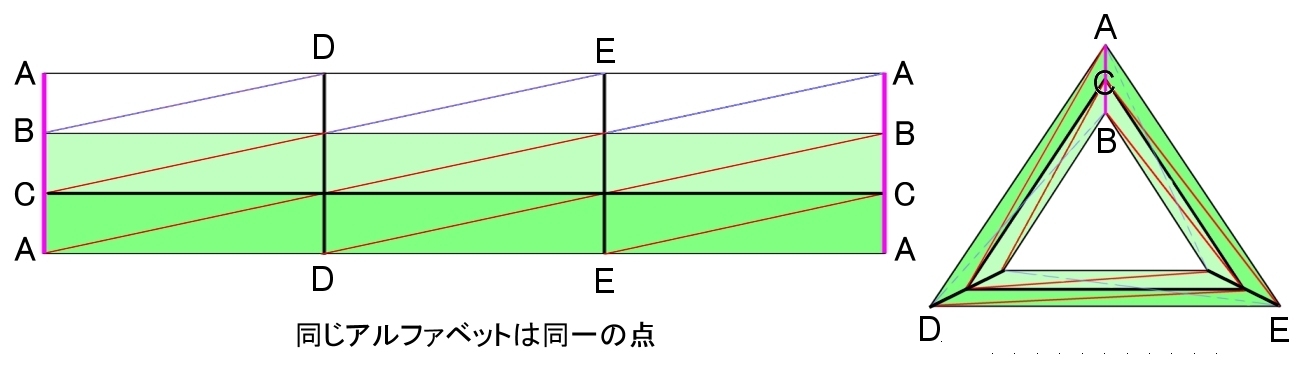
さらに,K の2回重心細分K”に関する星状多面体|Star(pσ;K”)|を考えます。
ただし,pσは複体K の各単体 の重心 (図中赤点で示す)
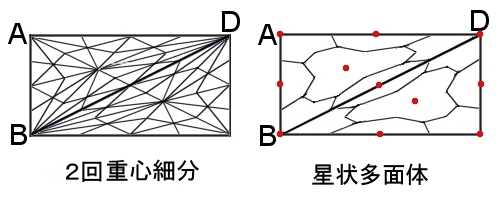
すると,PLトーラスのそのような星状多面体,
U |Star(pσ;K”)| σ∈K
による分割が下図のように得られます。(↓点線はもとの複体)
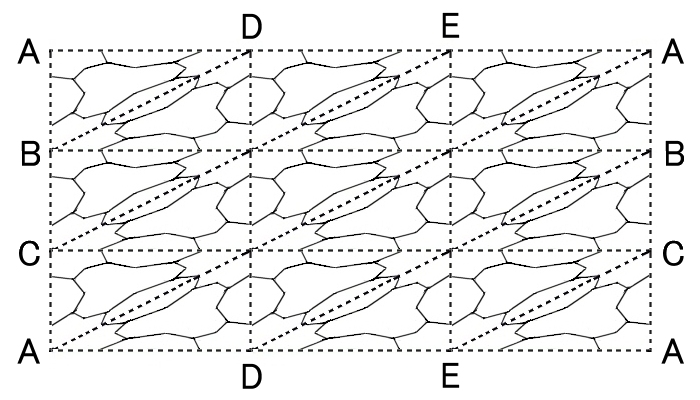
[3] 複体K の1次元部分複体 L の中で,|L|が連結で,かつループを含まないとき,L を樹木といいます。特に樹木のうち,すべての頂点を含む樹木は極大樹木といいます。
下図はトーラスの複体Kについて,一つの極大樹木を黒い太線で示しています。
また,Lの単体σの重心pσのK”の星状多面体のすべてのσ∈L についての和集合,
U |Star(pσ;K”)| σ∈L
を導近傍といい,N(L;K)と表します。トーラスの複体K では,上図のグレーで示した部分となります。この部分は弧状連結で,2次元円板Δ2に位相同型です。
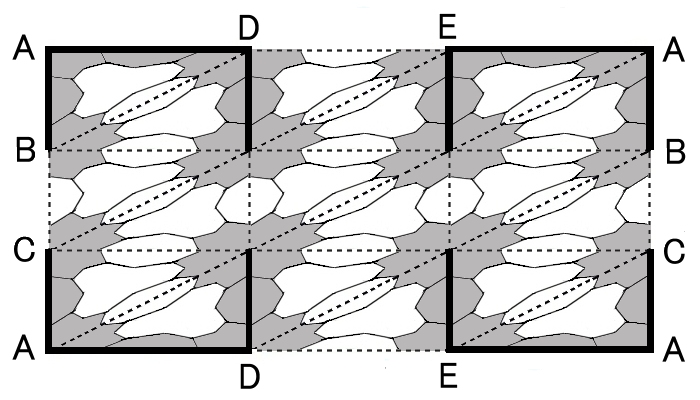
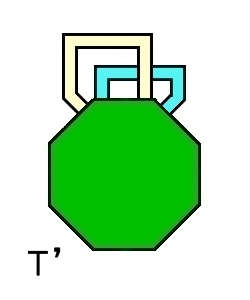
[4] 星状多面体で分割されたPLトーラスから上記の導近傍 N(L;K) の内部を取り除いた残りの部分|T’|
を考えます。
その部分は下図で着色された部分です。
 |
⇔ PL 同相 |
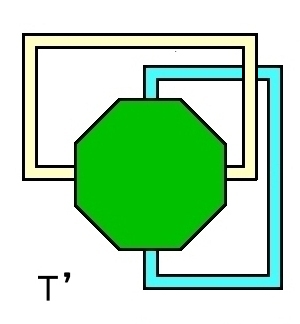 |
| |T’| =|T2|−Int N(L;K) 穴あきトーラス [S1,1] | ||
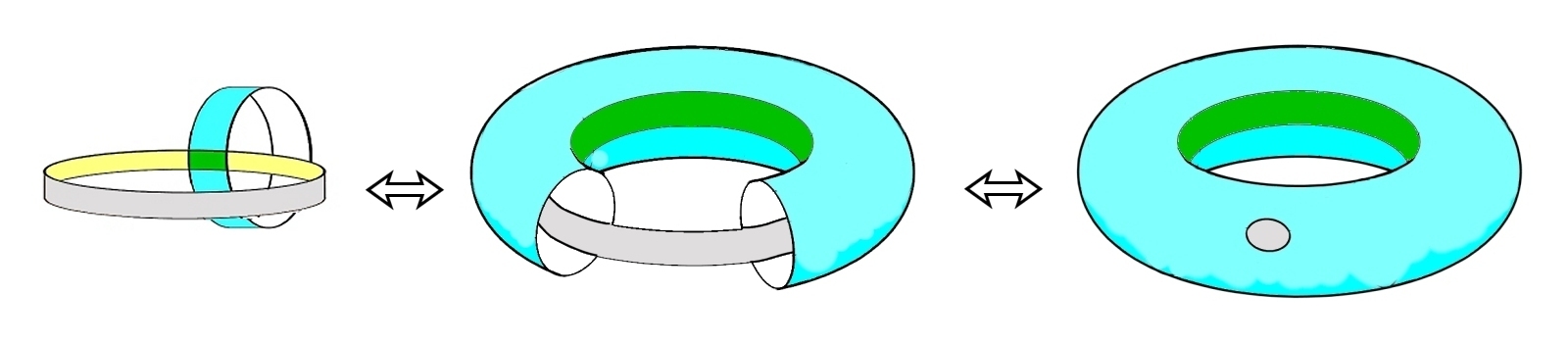
言うまでもなく,この|T’| はトーラス面から開円板を取り除いた図形に位相同型です。下図を見て確認。
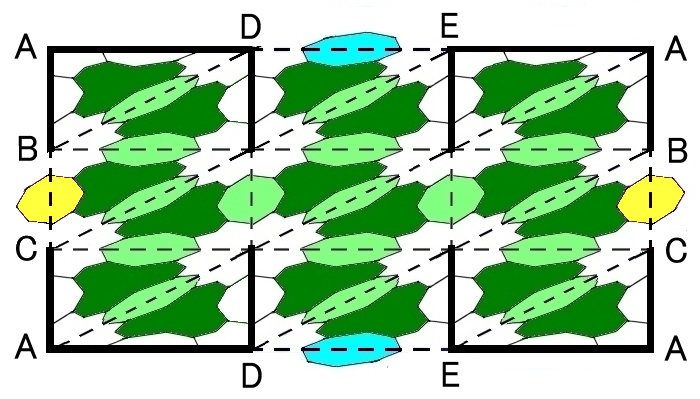
|T’| は次の2つのタイプの多面体に分けられます。
国 : 2単体の重心の周りの|Star(pσ2;K”)|をこう呼び,濃い緑で示す。
橋 : 1単体の重心の周りの|Star(pσ1;K”)|をこう呼び,黄緑,黄,水色で示す。
国と国は橋を介して繋がっていることが分かります。そして橋はさらに3つの種類があります。
任意の国を起点として橋を渡った隣国を順々に連邦国家としてすべて統一していきます(侵略じゃないよ!)。そのときのルールとして,連邦国家の内部に空白が生じないように,つまり,国たちと橋たちでループを作らないようにします。
上に示した|T’| の図でいえば,濃い緑と黄緑を合わせた部分が連邦国家です。
残った2つの橋(黄色橋と水色橋)が連邦に属さないループを形成するループ橋で,それらを引き延ばして表した位相同型な図形がその右側に示した T’です。ループ橋はバンドと呼ぶことにします。
[5] 次に連結したト−ラス面を考えましょう。
g個の穴あきトーラスを繋ぎ合わせた下図は一つの境界S1をもつ2次元多様体 [Sg,1] です。
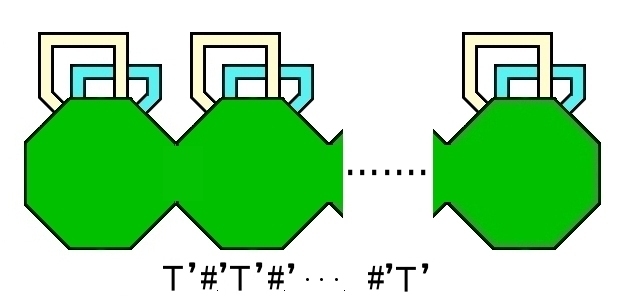
この境界 (よく見ると境界は1本の閉曲線であることが確かめられます) に開円板を張り合わせて穴を塞ぐと,g個のトーラスが連結された2次元閉多様体 [Sg,0] となります。
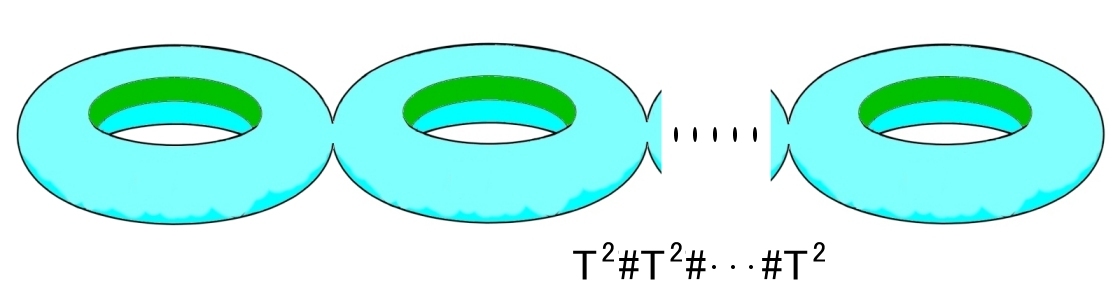
[6]
(7) クラインの壷 から1つの開円板を取り除いた図形 K’はトーラスの場合と同様に考えて下図のようになります。
ただし,四角形全体の左右の辺は半回転ひねってから繋ぐ必要があるので,紫色で示した橋は隣り合う国と国を半回転ねじれたバンドで繋がっていると考える必要があります。
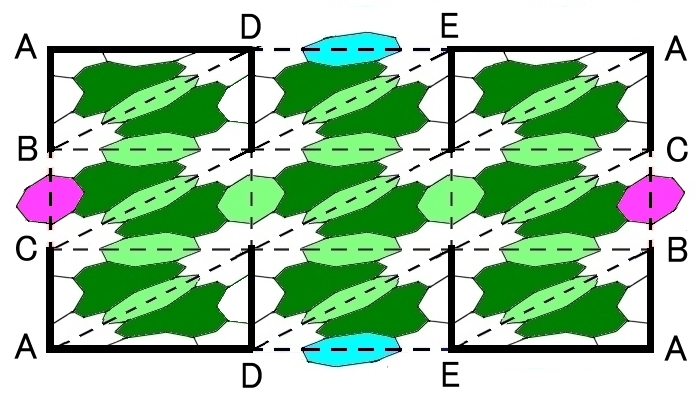 |
⇔ PL 同相 |
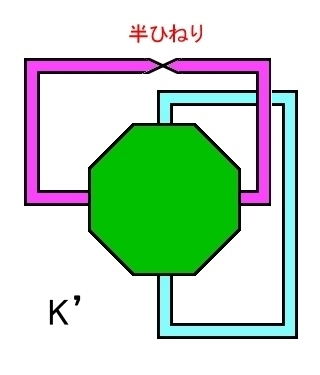 |
| K’=K−IntΔ2 穴あきクラインの壷 [N2,1] | ||
ここで得られた穴あきクラインの壷 K’はさらに以下に示されるように繋がった2つのメビウスの帯 M#'M [N2,1] とPL同型です。
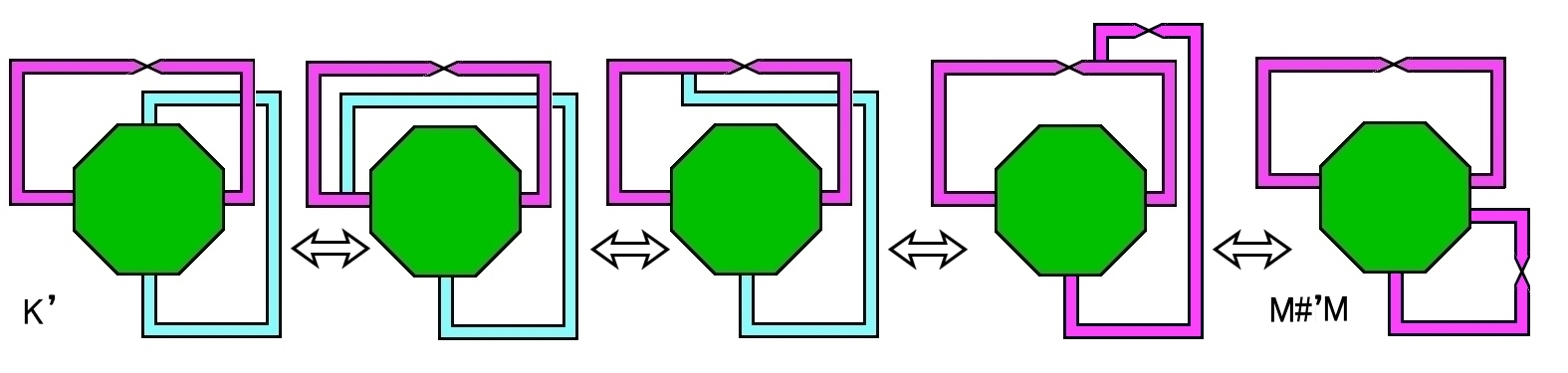 |
| 水色のバンドをメビウスの帯(紫)の境界をすべらせ,位相同型を保ったまま移動させている。 |
K’=M#'M=P’#'P’ と位相同型な曲面は下図のように表せます。
 |
⇔ | 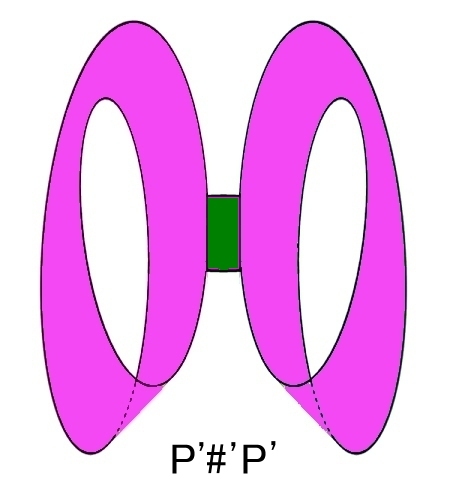 |
⇔ | 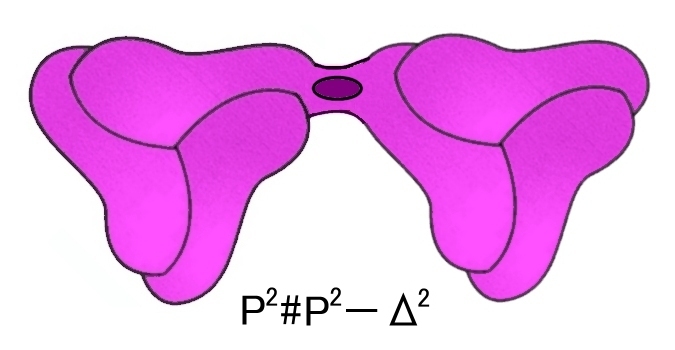 |
|
| K’=K−IntΔ2 | P’#'P’ | P2#P2−IntΔ2 |
穴あきクラインの壷 K’は2つの射影平面 P2からそれぞれ開円板を取り除いてできるメビウスの帯の周囲(=S1)の一部分どおしを濃緑で示した部分で繋げた図形 (P’#'P’=M#'M) と位相同型となります。また,これは2つの射影平面どおしを連結した多様体から開円板を一つ取り除いた多様体 P2#P2−IntΔ2とも位相同型です。
すなわち,クラインの壷 K は2つの射影平面の連結和 P2#P2 と位相同型です.
K’ 〜 P’#'P’
↓ Δ2を張り合わせてフタする。
K 〜 P2#P2
[7]
T’と P’ が連結した図形は
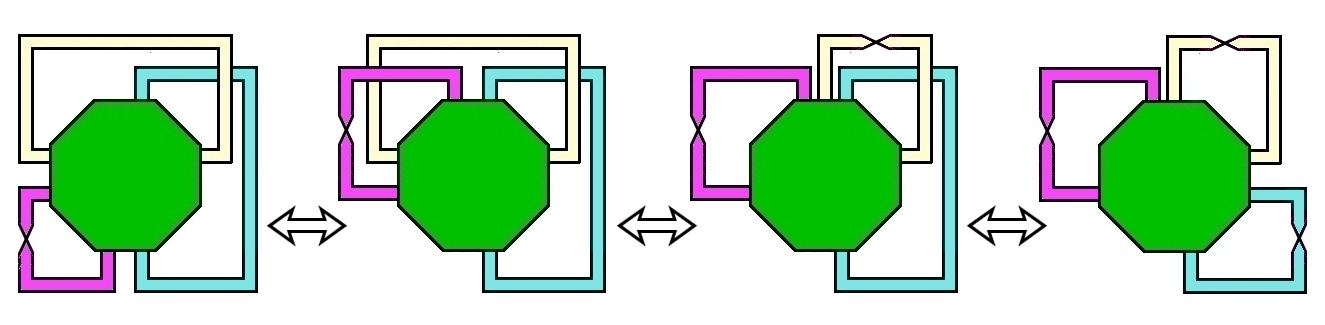
のように位相同型を保ったまま変形できます。すなわち,
T’#'P’ 〜 P’#'P’#'P’
↓ Δ2を割り合わせてフタする。
T2#P2 〜 P2#P2#P2
⇒ P2 とT2 が連結した多様体は,
T2を2個の P2 に置き換えても位相同型である。
すなわち,この操作でトーラスと射影平面を含む2次元閉多様体は,一つでもP2が連結されていれば,すべて射影平面 P2 だけが連結された多様体に位相同型を保ったまま変形できることが分かります。
[8] 穴あき射影平面を h 個だけ繋ぎ合わせた下図は一つの境界 S1をもつ2次元多様体です。
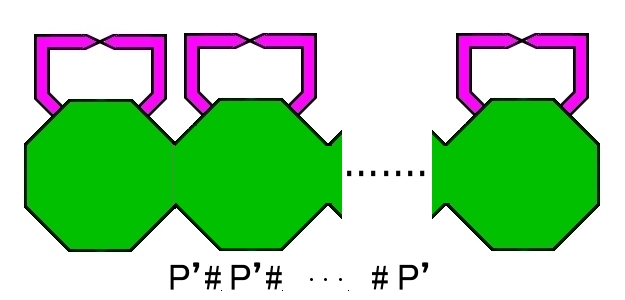
この境界に開円板を張り合わせて穴を塞ぐと,h個の射影平面が連結された2次元閉多様体 [Nh,1] となります。
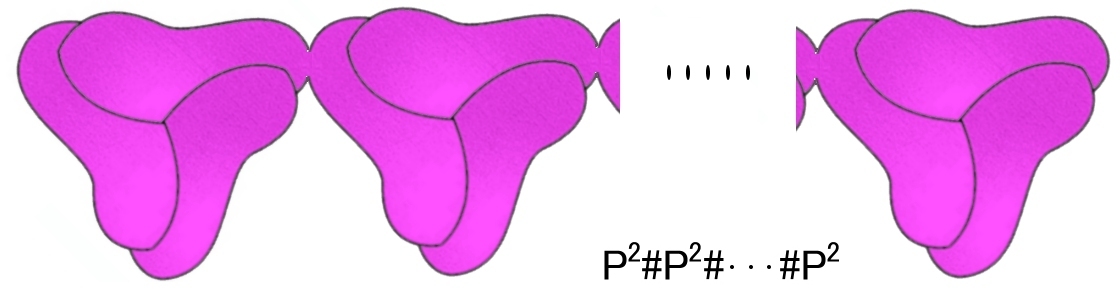
この閉多様体はh個の射影平面を連結して作られる閉多様体 [Nh,0] と位相同型です。
連結した射影平面 P2の個数 h も2次元閉多様体の種数と呼ばれます。
[1] ここまでの考察をすべて考慮すると,2次元多様体は次の3つパーツと穴を塞ぐΔ2を基に構成できることが分かります。
 |
 |
 |
||
| 境界S1 | 境界S1 | 境界S1×2 | ||
| 穴あきトーラス | 穴あき射影平面 | アニュラス |
一般的な構成方法としては,
gT’ ≡ T’#'T’#'…#'T’ (T’がg個連結)
hP’ ≡ P’#'P’#'…#'P’ (P’がh個連結)
bR ≡ R #' R #'…#' R (P’がb個連結)
(gT’)#'(hP’)#'(bR) = b+1個の穴の空いた2次元多様体
↓ Δ2で必要な分だけ穴を塞ぐ
任意の2次元多様体
これでもいいのですが,実際は P2 と T2 が連結して混じり合っている場合は,すべて P2 のみが連結した曲面に位相同型であるから,結局,T2 だけ,もしくは P2 だけを含む2次元多様体を標準形とする分類が行われます。
すなわち,閉曲面の場合であれば,
|
定理 閉曲面(2次元閉多様体)の標準形 向き付け可能で連結な閉曲面は, g 個のトーラスが連結した gT2 (g≧0) と同相である.ただし,g=0 は球面 S2 。 向き付け不可能で連結な閉曲面は, h 個の射影平面が連結した hP2 (h≧1) と同相である。 |
ここで,g および,h を閉曲面の種数といいます。また,記号は,
gT2 ≡ T2#T2#…#T2 (T2がg個連結: 種数gのトーラス)
hP2 ≡ P2#P2#…#P2 (P2がh個連結: 種数hの射影平面)
という意味です。
命名の問題ですが,
種数 g のトーラス ⇒ 向き付け可能な種数 g の閉曲面
種数 h の射影曲面 ⇒ 向き付け不可能な種数 h の閉曲面
の方がベターなのかもしれません。
[2] 境界がある(穴があいている)曲面を含める場合は R を連結しても構わないので,そのRの個数を b として,
(gT’)#'(bR) または, (hP’)#'(bR) の穴の一つをΔ2で塞ぐと考える↓
|
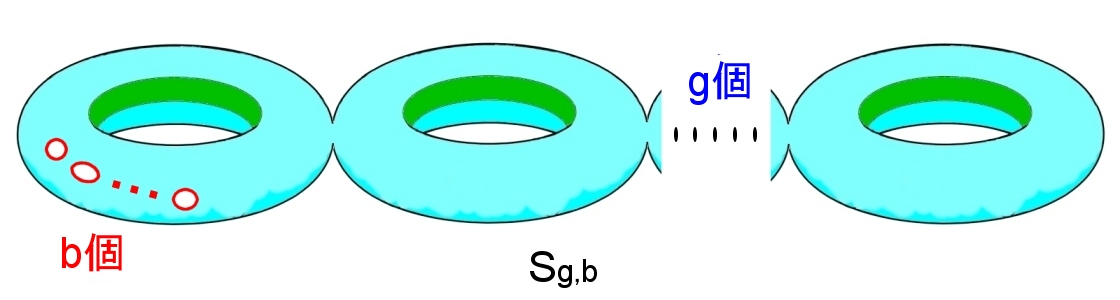
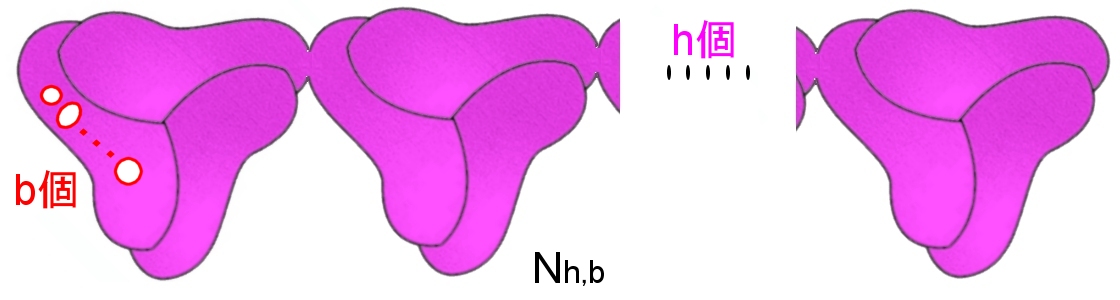
定理 一般的な2次元多様体の標準形 向き付け可能で連結な2次元多様体は,種数 g,境界(〜S1)の個数 b であれば, Sg,b ; g=0,1,2,…, b=0,1,2,… 向き付け不可能で連結な2次元多様体は,種数 h,境界(〜S1)の個数 b であれば, Nh,b ; h=1,2,…, b=0,1,2,… のいずれかに同相である。 |
ここで,Sg,b は下図のような曲面です。
Nh,b は下図のような曲面です。
[3] 関連した定理,
|
定理 2つの2次元多様体が同相となるための必要十分条件は, (1) どちらも同じオイラー標数をもつ。 をみたすことである。 |
証明はもう少し後の方でします。