|
５ カルノーサイクル | |
| f-denshi.com ［目次へ］ 更新日：08/10/20 カルノーの話を付け加えました。 | ||
| サイト検索 | ||
１．カルノーサイクル ［熱効率最大の理想的熱機関］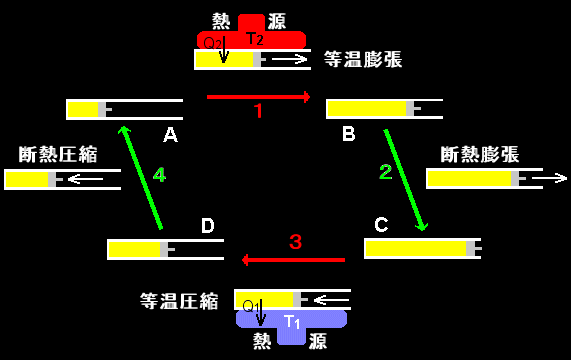
［１］ カルノーサイクルとは，高熱源から熱を受けとりながら外部に仕事を行い，低熱源に廃熱を捨てながら元の状態に戻るという熱機関の働きを熱力学的に見たらどうなるのかを単純化したものです。もし，本当にカルノーサイクルを実現できたならば，それは最高の効率をもつ究極の熱機関であることもわかっています。しかし，カルノーサイクルが熱力学において非常に重要な地位を占めている理由は別にあって，エントロピーを熱力学の体系に自然な形で導入（定義）するために欠かせない存在だからです。このような背景は熱力学が構築された当時からずっと変わっていないでしょう。現実の内燃機関に使われているサイクルとしてはオットーサイクル，ディーゼルサイクル，ブレイトンサイクル，ランキンサイクルなどがありますが，ここでは詳しく述べませんので興味のある方はネット検索等で調べてみてください。
ここではカルノーサイクルについてだけ比較的詳しく述べます。カルノーサイクルは右のような２つの熱源に接触ができるピストン付きのシリンダーに入った理想気体を準静的に，４つのステップにしたがって膨張-圧縮させて元の熱平衡状態に戻るサイクルから構成されています。順を追って書くと，
１．まず，始状態A（VA,PA,T2）から等温膨張させて状態B（VB,PB,T2）にします。
２．次に断熱膨張させ，状態C（VC,PC,T1）にします。この過程で温度がT2からT1へと低下します。
３．今度は等温圧縮を行い状態D（VD,PD,T1）とします。
４．そして最後に断熱圧縮を行うと温度も上昇し，ぴったり状態A（VA,PA,T2）に戻ってくる。
というのがカルノーサイクルです。このとき，各ステップで仕事と熱量が出入りしますが，それを表にまとめると次のようになります。
| 過程 | 準静的変化 | 条件 | 受けとる仕事 | 受けとる熱量 |
| １ A⇒B | 等温膨張 | dU＝0 | W1＜0 | Q2＞0 |
| ２ B⇒C | 断熱膨張 | d'Q＝0 | W2＜0 | 0 |
| ３ C⇒D | 等温圧縮 | dU＝0 | W3＞0 | Q1＜0 |
| ４ D⇒A | 断熱圧縮 | d'Q＝0 | W4＞0 | 0 |
もちろん，サイクルがきちんとループを描くためには，出入りした仕事や熱量は全く自由な値を取ってよいわけではなく，全体として熱力学第１法則： W1＋W2＋W3＋W4＋Q1＋Q2 ＝dU ＝0 を満たしていなくてはいけません。また，この１サイクル（ A→B→C→D→A ）において系は，
「高熱源からQ2の熱を受けとり，−Σ Wj の仕事を外部に行い低熱源に |Q1| の熱を渡す。」
ということを行っていますが，これを大雑把に見れば，「燃焼によって発生した熱Q2を利用して外部へ動力，｜W1＋W2＋W3＋W4｜を出力し，エネルギーの一部を廃熱｜Q1｜として外へ捨てることで，スタートの状態へ戻るエンジン」と考えることができます。ちょっと現実離れしていて苦しいかな？
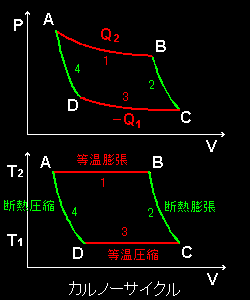
また，このサイクルを横軸を体積V，縦軸を圧力PとするP-V線図として描くと，等温過程より断熱過程の方が急な傾きを持つ[#]ことから右のようになります。その下にはT-V線図も参考のために示しています。
［２］ それではこれらの図を参考にしながら，１サイクルにおける熱，仕事の出入りをステップごとに熱力学第一法則 [#]，理想気体の状態方程式を用いて詳しく計算してみましょう。↑外部から受け取る仕事，および，熱量に対して正の符号をとることに注意
［準静的等温過程の仕事，熱量の計算］
まず，過程１における等温膨張と等温圧縮過程について系がする仕事を計算します。
理想気体の等温過程では dU＝0 なので[#]，d'W ＋d'Q＝0 ．
過程１： −（受けた仕事 W1）＝（受け取る熱量Q2）
（実際は外に−W1の仕事を行う）
| −W1 ＝ |  |
PdV ＝ |  |
 |
nRT2 |  |
dV ＝nRT2log | |
VB | |
＝Q2 |
| V | VA |
以上のようになりますが，カルノーがなぜ等温過程を持ち出したのか想像できますか？理想気体の内部エネルギーは温度だけの関数なので等温過程ならば，dU＝0です。そしてこのとき，-d'W＝d'Qが成り立ちます。つまり，過程１：A→Bにおいて，与えられた熱量は100％すべて外部への仕事に変えられるわけです。カルノーはもちろん熱力学第一法則は知らなかったのですが，この関係式は正しく見ぬいていました。パーフェクトな変換効率ですね。ところが，効率100％はすばらしいのですが，ピストンを元の位置Aに戻すために同じ温度（T2）で可逆的に圧縮，逆行させると，往きと同じだけの仕事を系に与えてやらければなりません。もちろんこれでは，プラマイゼロで熱機関から正味の仕事を取り出すことができません。外への仕事が正として残るためには，帰りの仕事をなるべく小さく押さえなければいけませんが，その解決手段は，今導いた式を見ればすぐにわかるように温度T2を低下させてやることです。
では，具体的にどのような手段で系の温度を低下させたら熱機関にとって好都合なのでしょうか？その手段として，シリンダを低熱源に順々に接触させて熱を奪うなどという無粋なことをカルノーは考えませんでした。もし，高温の気体の入ったシリンダと低温の熱浴を直接接触させると，仕事に寄与しない単純な高温から低温への熱の移動（＝熱伝導）が生じ，それは熱機関としてはエネルギーのロス以外何ものでもないと考えたからです。実際，その当時の蒸気機関では，せっかく石炭を燃焼して作り出した高熱蒸気を水で冷却する工程が含まれていました。それを見ていたカルノーは「なんて無駄なことを！」と考えていたに違いありません。そこで登場するのが断熱過程です。温度差のある物体どおしの接触を回避しながら系の温度を下げる方法です。
［準静的断熱過程の仕事の計算］
断熱膨張過程です。断熱ですからここで新たに投入する熱はゼロであり効率的です。断熱膨張で系が行う仕事は理想気体に対する断熱曲線[#]
PV γ＝PBVBγ＝PCVCγ ＝定数 より
過程２ 外へする仕事 −W2
| W2 ＝− |  |
PdV ＝− | |
|
PBVBγ | |
dV ＝−PBVBγ | |
1 | − | 1 | |
| Vγ | （1−γ）VCγ-1 | （1−γ）VBγ-1 |
| ＝ | 1 | （PCVC −PBVB ） |
| γ−1 |
↓ 状態方程式： PBVB＝nRT2，PCVC＝nRT1 を用いて，
W2 ＝ nR （T1−T2） ( ＜ 0 ) γ−1
となります。次の過程３のために温度をT1へ下げたのですが，タダで仕事も取り出せたのでちょっと得した気分です。
［２．１］ 今度はピストンを元の位置に戻すために気体を収縮させていきます。収縮は先程述べたようになるべく低い温度T1で等温圧縮します。
過程３ （受けた仕事 W3）＝−（受けた熱量Q1）
（実際は外に−Q1の熱を放出）
| W3 ＝− |  |
PdV ＝− | |
|
nRT1 | |
dV ＝-nRT1log | |
VD | |
＝−Q1 |
| V | VC |
もちろん，ここでC→Dへ圧縮した時の体積VDは，理想気体を状態Aから温度がT1に下がるまで断熱膨張させたときにとる体積と等しくなければいけません。
過程４ 系にする仕事
この断熱圧縮過程も過程２と同様に計算できて，
W4 ＝ nR （T2−T1） γ−1
注意：断熱自由膨張[#]とは違って，ここでの可逆な断熱膨張・収縮過程では外界に仕事をしたりされたりしています。
となります。ということは，W4＝−W2で，先程過程２においてタダで得た仕事と同じだけここでは系に仕事を返してやらなければいけません。差し引きゼロです。つまり，２つの温度間を可逆かつ，断熱的に往復しても仕事に関しては損得なしです。
［2S］ 以上のエネルギーの出入りをまとめると，
| j | 過程 | Wj | Q |
ただし，
が成り立つ[#]。 |
||||||||||||
| 1 | PV ＝一定 |
|
|
|||||||||||||
| 2 | PVγ＝一定 |
|
0 | |||||||||||||
| 3 | PV ＝一定 |
|
|
|||||||||||||
| 4 | PVγ＝一定 |
|
0 | |||||||||||||
［３］ ここで，熱機関の効率を次のように定義します。
η ＝ 外部になした正味の仕事 高温熱源から受け取った熱量
カルノーサイクルに関しては，
η ＝ −（ W1＋W2＋W3＋W4 ） Q2
↓ W1＋W2＋W3＋W4＋Q1＋Q2 ＝ 0 （ ＝dU ） ［ 第一法則 [#] ］ から
＝
Q1＋Q2 Q2
［４］ さらに，この式は温度で書き直すことができます。そのためには， B→C，D→A の断熱曲線 [#] ，
T2VB γ-1 ＝ T1VC γ-1
T1VD γ-1 ＝ T2VA γ-1⇒
VB ＝ VC VA VD
を利用します。これを用いると，カルノーサイクルの熱機関としての効率は，
| η＝ |
|
＝ |
|
||||||||||||||||||||||||
＝
T2−Ｔ1 ＝ 1−
Ｔ1 T2 T2
となります。もちろん，最後の値は1より小さな値しか取り得ません。T1は低熱源の温度，これはふつう大気の温度３００Kと考えてよいので，効率を高くするためには高熱源の温度を高くすればよいこともわかります。
［５］ まとめです。
|
熱効率： および，（上の ＝ から ）
|
最後の（２）式は後にクラウジウスがエントロピーと呼ぶことになる量に対応しています。
以上，現代的な知識に基づいてカルノーサイクルを説明しましたが，カルノー自身は熱力学第１法則，第２法則いずれの発見者ということにもなっていません。彼は高温から低温への熱の移動量と仕事量が等価であることを見抜いていました。また，準静的な過程と呼ばれる過程を用いることで熱機関の熱効率が最大となることも彼の着想です。ただ，熱素説の影響から抜け出すことができなかったのか熱量は高温から低温へ移動するだけで不滅と考えていました。つまり，|Q1|＝Q2としてしまったのです。そのため熱力学第１法則のようなつじつま合わせができなかったのです。しかしながら，発明家に対しては１００点の答案，科学者に対しては９９点の解答を残しました。そしてカルノーは早世します。
