| B3 電解液中のイオン輸送過程 | |
| f-denshi.com [目次へ] 更新日: 04/1/4 | |
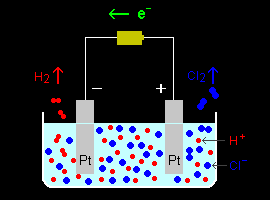
[1] 塩酸水溶液( aq HCl )に浸した2本の白金電極に電圧をかけておこなう塩素電解を例にとり、電解液中での物質移動過程を考察します。(同時に起こる水の分解反応は無視します。)この電解では各電極上で次の反応が起こっています。
正極: 2Cl- → Cl2 (気体発生)+ 2e- (酸化反応)
負極: 2H+ + 2e- → H2 (気体発生) (還元反応)
このとき、電解液中のイオンの挙動に着目すると、正極表面ではCl-イオンが消耗され、Cl-の不足が生じ、一方、負極表面では、プロトンH+が消費され、H+の不足することが容易に予想できます。もちろん、この不均衡は電気的中性を維持するために、ただちに電解液中に溶解している正負イオンの再分布によって修復されなければいけません。その過程は物質輸送過程と呼ばれ、つぎの3つに分けて考えることができます。
1.拡散 ( diffusion ):拡散はすべての粒子がもっている熱運動による運動。
2.泳動 ( migration ):泳動は溶液中の正味の電場が荷電粒子に及ぼす力による運動。
3.対流 ( convection ):対流は溶液が流動することで引き起こされる撹拌
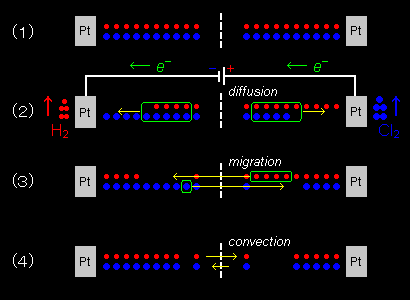 これらの過程はふつう同時に進行しますが、ここでは右図に従って順に解説いたします。
これらの過程はふつう同時に進行しますが、ここでは右図に従って順に解説いたします。
[2] 電解開始前の電解液中の正負イオンは、均一に分布しており、電解質濃度も電解槽内で均一です。
| (1) | |
| ↓ | 電解を始めると、正極表面付近では、Cl-が酸化され、負極ではH+イオンが還元されて消滅していきます。 |
| (2) | |
| ↓ | これを補う主な電解質の供給機構はイオンの拡散(diffusion)によります。しかし、正負イオンとも同じように生じる拡散は、電気的な中性の回復にはあまり寄与しません。 |
| (3) | |
| ↓ | マクロな電気的中性の回復は電場による荷電粒子の移動である泳動(電気泳動)によって達成されます。 |
| (4) |
電流密度が低いときは、以上の3つの過程を考えれば十分ですが、電流密度が高い場合は、電解液の対流が引き起こされ、電解質濃度の均一性の保持はもっぱらこの対流による撹拌効果によることとなります。
[3] 上図の(3)に示しているように、泳動による電荷輸送現象(イオン伝導)には正負イオン種が同程度に寄与するわけではありません。この例の場合、質量の小さいプロトンは塩素イオンに較べて、早く動き、溶液中での電荷輸送の中心的な担い手となっています。その割合は、この系では全電流の約80%を占めていることが知られています。全イオン電流に対する各イオン電流の分率を輸率 ( transport number ) tj といい、
tH+ = 0.8、 tCl- = 0.2
のように書きます。 正確な定義はこちら 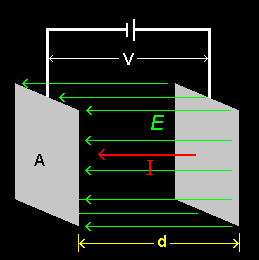
[4] さて、右図に示すような距離 d だけ離しておかれた面積 A の2枚の電極の間に電圧 V をかけたときに流れる電流値 I から計算される抵抗を R ( = V / I )としましょう。イオン電流は必ずしもこの電極間を直線的に流れないであろうし、オームの法則が ”よく” 成り立つ保証などありませんが、金属の電気抵抗を模して比導電率( conductivity )κを次のように定義します。
I = 1 = L =κ A ⇔ κ= d [Ω-1cm-1] V R d RA
ここで、κは、「単位電場(V/d=1)をかけたときに電解液中に流れるイオン電流密度」とみなせることも覚えておきましょう。
[5] さらに、単位電場のもとで泳動するのイオンの限界速度=移動速度( mobility )u [cm2V-1sec-1]を用いてκを表してみましょう。
(単位電場中でのイオンの限界速度は、Stokesの法則より force=|z|eE=6πηrv )
それは物質 j の価数を zj、濃度を Cj、移動度 uj をその種が担う部分電流を ij とすると、
κ = F |zj|uj Cj ← κ = Id/VA、 V/d = 1、 I = A | zj | F・Cjuj より
で与えられます。ここで、F はファラデー定数です。
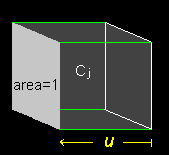 |
| 面積1を通過するイオン種 j の 量はuj ・Cj |
[6] さらに、正負それぞれ1種類のイオンしか含まない(HCl 水溶液のような)単純な電解液の場合、正電荷、または負電荷の濃度を、
Ce =|zj| Cj
と表して、当量イオン伝導度 Λ を次のように定義します。
Λ = κ = F ( u+ + u- ) = λ+ + λ- Ce
ここで、λ+ = F u+ は陽イオンの当量イオン伝導度で、「 陽イオンが寄与する単位電場、単位陽イオン濃度あたりの電流密度 」 を表します。(λ- も同様。) これを用いて輸率はそれぞれ、
t+ = λ+ = u+ : t- = λ- = u- Λ u+ + u- Λ u+ + u-
と定義します。