調和振動子　３
f-denshi.com  更新日：05/04/14
サイト検索

１．調和振動子の時間発展

[１]　前ページで時間発展についての基本的な知見を得たので，早速，調和振動子のダイナミックな挙動に適用して見ましょう。最初に消滅･生成演算子と位置･運動量の４つの演算子の関係を再確認しておくと [#]，[#]，

a ＝ mω 2h  x＋ i p mω a†＝ mω 2h  x− i p mω

x＝ h 2mω (a＋a†)  p＝i mωh 2 (a†−a)

となります。しかし，ここではこのすべての演算子は時間依存性をもつハイゼンベルク表示 [#] におけるものと読み替えます。つまり，このページの演算子，a は前ページの記号では a_H を意味します。

[２]　さて，１次元調和振動子を前ページの(２)式[#](＝ハイゼンベルグ運動方程式)に適用してみましょう。
　　　　(ここでの p は p_x と同じ意味)

dp	＝	1	[p ,H]＝	1	[p ,V(x)]＝		−	∂V(x)		＝−mω2x　････(１)
dt		ih		ih				∂x

ここで，調和振動子のハミルトニアン[#]が，

H＝	p2	＋V(x)　；　　　V(x)＝	mω2x2
	2m		2

であることを用いています。

[２]　この(１)と，

m	dx	＝p
	dt

を用いて，消滅演算子の時間微分は次のように変形できます。

da dt

＝

mω 2h

d dt

x＋

i p

＝

mω 2h

p

＋

i (−mω2x)

mω

m

mω

＝	mω 2h	(−iω)		i p	＋ x		＝−iωa　              ････(３)
				−iωm

という微分方程式が得られます。同様に，

da†	＝   ･･　同様に↑　･･   ＝i ωa†　　　　　　　　 ････(４)
dt

これらの解は，

a(t) ＝a(0)ｅ^{−i ωt}
a^†(t)＝a^†(0)ｅ^{i ωt}

となります。冒頭に与えた関係を用いて x，p で表すと，

a(t) ＝

mω 2h

x(t)＋

i p(t)

＝

mω 2h

x(0)＋

ip(0)

ｅ−i ωt

mω

mω

a†(t)＝

mω 2h

x(t)−

i p(ｔ)

＝

mω 2h

x(0)−

ip(0)

ｅi ωt

mω

mω

[３]　さらに，この２式（中辺＝右辺）を x(t)， p(t)　について解くと，

という位置演算子，運動量演算子の時間発展を表す式が得られます。

　　ここで，注意してほしいのは，演算子 x(t)，p(t) が振動しているからといって，位置や運動量の期待値がいつも振動しているわけではないということです。たとえば，定常状態(⇒ひとつの固有状態|n＞)にある位置の期待値は，

＜n|x(t)|n＞＝＜n|x(0)|n＞cosωt ＋	＜n|p(0)|n＞	･sinωt ＝0
	mω

であり[#]，振動しているわけでないのです。どのようなときに期待値が振動するかといえば，時刻 0 における状態ケットが固有ケットの線形結合で表せるときです。

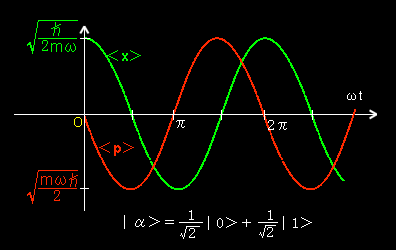
２．非定常状態

[１]　時刻 t＝0 において，調和振動子の固有ケット，|0＞と |1＞ との１次結合，

|α＞＝c₀|0＞＋c₁|1＞　　　　　　     　･････ [***]

で表せる ”振動状態” を考えます。 ここで，係数は，

c₀＝r₀･exp (iθ₀)，
c₁＝r₁･exp (iθ₁)，　ただし，　r₀²＋r₁²＝1，および，　r₀ ，r₁ ≧0，

とします。この状態の位置 x の期待値を計算してみましょう。

＜α|x|α＞＝＜α|	h 2mω	(a＋a†) |α＞

＝	h 2mω		c0*c1＜0|a|1＞＋c0c1*＜1|a†|0＞

＝	h 2mω		r0･r1･exp (-iθ0)exp (iθ1)＋r0･r1･exp (iθ0)exp (-iθ1)

＝	h 2mω		2r0r1･cos (θ0−θ1)		･････(５)

同様に[#]，        ↑　　＜α|x|α＞≡＜α|x(0)|α＞≡＜α，0|x|α ,0＞　というイミ。

＜α|p|α＞＝＜α|i	mωh 2	(-a＋a†)|α＞

                      ･･･････････　省略　･････････････

＝	mωh 2		2r0r1･sin (θ0−θ1)		･････(６)

[２]　したがって，[*]，[**] より，

＜α|x(t)|α＞＝＜α|{　x(0)cosωt ＋ (p(0)/mω)sinωt　}|α＞　　　　　　　　　　　　　　　　　

＝＜α|x(0)|α＞cosωt ＋	＜α|p(0)|α＞	sinωt
	mω

＜α|p(t) |α＞＝＜α| {−mωx(0) sinωt＋p(0)cosωt　}|α＞　

                ＝−mω＜α|x(0)|α＞sinωt ＋＜α|p(0)|α＞cosωt　

＜α|x(t)|α＞＝　       ＜α|x(0)|α＞ cosωt  ＋ ＜α|p(0)|α＞  sinωt mω ＜α|p(t) |α＞＝−mω＜α|x(0)|α＞ sinωt  ＋　＜α|p(0)|α＞ cosωt

さらに，|α＞ ＝ c₀|0＞ ＋ c₁|1＞　に対して計算を進めれば，

＜α|x(t)|α＞＝2r0r1･	h 2mω		cos (θ0−θ1)cosωt ＋ sin (θ0−θ1)sinωt

＜α|p(t) |α＞＝2r0r1･	mωh 2		−cos (θ0−θ1)sinωt ＋ sin (θ0−θ1)cosωt

[３]　再び，[*]，[**]　から，

x(t)2＝x(0)2cos2ωt＋	p(0)2	sin2ωt＋	x(0)p(0)＋p(0)x(0)	cosωtsinωt
	(mω)2		mω

p(t)²＝(-mω)²x(0)²sin²ωt＋p(0)²cos²ωt−mω{x(0)p(0)＋p(0)x(0)}cosωtsinωt

と計算しておきます。ここで，|α＞＝c₀|0＞＋c₁|1＞ に対して，

＜α|{xp＋px }|α＞＝0          ←　xp＋px＝ih (−a²＋a^†2 )　　なので [#]

を用いれば，

[４]　さらに，

x(0)2＝	h	(a2＋a†2＋a†a＋aa†)，　　　p(0)2＝	−mωh	(a2＋a†2−a†a−aa†)
	2mω		2

をもちいて，|α＞ ＝ c₀|0＞ ＋ c₁|1＞について，

＜α|x(0)2|α＞＝	h	(1＋2|r1|2)，　   ＜α|p(0)2|α＞＝	mωh	(1＋2|r1|2)
	2mω		2

と計算できるので，

＜α|x(t)2 |α＞＝	h (1＋2|r1|2) 2mω	cos2ωt ＋	mωh (1＋2|r1|2) 2	1	sin2ωt
				(mω)2

＝	h	(1＋2|r1|2)
	2mω

のように計算できます。

[５]　＜α|p(t)² |α＞も同様で，以下これまでの結果をまとめます。

	位置　x	運動量　p
＜A(0)＞	h 2mω 2r0r1･cos(θ0−θ1)	mωh 2 2r0r1･sin(θ0−θ1)
＜A(t)＞	2r0r1 h 2mω {cos(θ0-θ1)cosωt＋sin(θ0-θ1)sinωt}	2r0r1 mωh 2 {−cos(θ0-θ1)sinωt＋sin(θ0-θ1)cosωt}
＜A(0)2＞	h (1＋2|r1|2) 2mω	mωh (1＋2|r1|2) 2
＜A(t)2＞	h (1＋2|r1|2) 2mω	mωh (1＋2|r1|2) 2

[６]　特別なケースとして，

|α＞ ＝		(A)	|0＞
		(B)	|1＞
		(C)	1 |0＞＋ 1 |1＞ 2 2

の３とおりの場合について具体的な計算結果を示します。

(C)は　＜α|x|α＞の最大値を与えるような状態ケットの条件となっていて，[***] は，　　　　

θ0＝θ1，　　　r0 ＝ r1 ＝	1
	2

のときに最大値，＜α|x|α＞＝			をとります。
		h 2mω

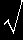一覧表です。

|α ,0＞ ＝	|0＞		|1＞		1 |0＞＋ 1 |1＞ 2 2
観測量A　＝	位置x	運動量p	位置x	運動量p	位置x	運動量p
＜A(0)＞	0	0	0	0	h 2mω	0
＜A(t)＞	0	0	0	0	h 2mω 　cosωt	− mωh 2  sinωt
＜A(0)2＞	h 2mω	mωh 2	3h 2mω	3mωh 2	h mω	mωh
＜A(t)2＞	h 2mω	mωh 2	3h 2mω	3mωh 2	h mω	mωh
＜(ΔA(t))2＞	h 2mω	mωh 2	3h 2mω	3mωh 2	h {1＋sin2ωt} 2mω	mωh {1＋cos2ωt} 2
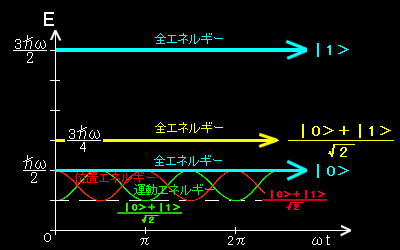
＜mω2x2/2＞ 位置エネルギー	hω 4		3hω 4		hω {1＋sin2ωt} 4
＜p2/2m＞ 運動エネルギー	hω 4		3hω 4		hω {1＋cos2ωt} 4
全エネルギー	hω 2		3hω 2		3ωh 4

＜(ΔA(t))²＞＝＜A(t)²＞−＜A(t)＞²

最初の状態|α＞が固有状態にあれば，位置エネルギー（ポテンシャルエネルギー），運動エネルギーの期待値は時間変化しませんが，状態ケットが，

２つの固有ケットを含む状態であるならば，運動エネルギーとポテンシャルエネルギーとの間でエネルギーのキャッチボールがおこなわれます。いわゆるマクロな系での「振り子運動」が観測されるのです。

[目次へ]

３．調和振動子のコヒーレント状態

形を変えずに振動する状態はコヒーレント状態と呼ばれ，消滅演算子の固有方程式となっている。ただし，固有値は実数ではなく，複素数となります。

a|λ＞＝λ|λ＞　　　　　　　　　　　　　　　　　[ 固有方程式 ]

|λ＞ ＝ exp		−|λ|2		eλa†|0＞
		2

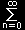＝		f(n)|n＞        　[ 固有関数 ]

ここで， f(n) ≡ exp		−|λ|2		λn
		2		n！

これは実際に a を作用させて，

a|λ＞　＝ exp		−|λ|2			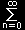λn	a|n＞
		2			n！

↓

a|n＞  ＝

n

|n-1＞

＝ exp		−|λ|2			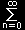λ･λn-1	a|n−1＞
		2			(n−1)！

|-1＞＝0　であることに注意して，和を　n-1　⇒　n　と書き直してとり，λをΣの外に出せば，

a|λ＞ ＝λ|λ＞

であることが確かめられます。λは複素数。

角運動量との類似性

＋，− で区別する独立した調和振動子の消滅，生成演算子を

a₊， a₊^† 　　( 調和振動子 ＋ に作用する )
a_-， a_-^† 　　( 調和振動子 − に作用する )

とし，これを用いて次の演算子を定義する。

J_＋ ≡ h a_＋^† a₋
J₋ ≡ h a₋^† a_＋

Jz ≡	h		a＋† a− − a−† a＋
	2

N ≡a₊，a₊^† ＋ a_-，a_-^† 　

J2 ≡Jz2 ＋	1		J＋J− ＋ J−J＋
	2

とするとき，

[J_z ，J_＋]＝hJ_＋  ；　[J_z，J₋]＝−hJ₋
[J² ，J_z]＝0

J2＝	h2	N		N	＋1
	2			2