一重項-三重項状態のエネルギー
f-denshi.com  更新日：

同一分子上にある一重項と三重項状態モデルのエネルギーについて考察してみます。

予備知識として，ハートリー・フォック近似法 ⇒ [#] を前提としています。

１．軌道関数も考慮したスピンの合成

［１］　まず，使用する記号について説明します。

多電子系波動関数のスレーター行列を用いた記法は，

Φ(r1，r2，････ ) ＝｜φaφbφc････｜≡	1 N！		φa(r1)	φb(r1)	φc(r1)	･･･
			φa(r2)	φb(r2)	φc(r2)	･･･
			φa(r3)	φb(r3)	φc(r3)	･･･
			：	：	：	･･･

ですが，スピンを考慮するときは，上向きのスピン関数をα，下向きをβとし，簡便に波動関数に添えるときは +，- と書いて

Φ(r₁，r₂，････ ) ＝｜φ_a⁺φ_b^-φ_c⁺････｜

≡	1 N！		φa(r1)α1		φb(r1)β1		φc(r1)α1		･･･
			φa(r2)α2		φb(r2)β2		φc(r2)α2		･･･
			φa(r3)α3		φb(r3)β3		φc(r3)α3		･･･
			：		：		：		･･･

のように書きます。

また，交換関係のときは， ( 反交換関係ではない )

　｜　　　|_p　：　スレーター行列式で，負の項の符号すべて＋に置き換える。

という記号を使用します。

［２］　電子1，電子2の２電子系の場合は，　　

｜φa+φb+｜＝	1 2		φa(r1)α1	φb(r1)α1		＝	1 2	(　φa(r1)α1φb(r2)α2−φa(r2)α2φb(r1)α1　)
			φa(r2)α2	φb(r2)α2

| φa+φb- |p　＝	1 2	(　φa(r1)α1φb(r2)β2＋φa(r2)α2φb(r1)β1 　)

と書くことにします。

一般的な場合は，スピン座標σを用いて，波動関数に番号 k，電子に番号 j を用いて， φ_k(r_j)χ (σ_j) のように書きます。

では計算を始めます。

［３］　まず，三重項からです。

三重項

２電子系　(He原子の励起状態を想定せよ) の場合に，φ_aφ_b軌道に入っている電子スピンがともに上向きの場合，(³Φ_k(r₁，r₂ ，σ₁，σ₂) ＝³Φ_kと記して，)

3Φ1＝｜φa+φb+｜

行列式で書くと，

3Φ1＝	1 2	φa+(r1) φb+(r1) φa+(r2) φb+(r2)

＝	1 2	φa(r1)α1 φb(r1)α1 φa(r2)α2 φb(r2)α2

展開して，

3Φ1＝ 1 2 ( φa(r1)φb(r2)−φa(r2)φb(r1) ) α1α2

と軌道関数とスピン関数を分離して書くことができます。

［４］　ここで，

J_- は合成スピンの | jm＞表示の　j　をそのままに　m　だけを一つ下げる演算子

昇降演算子 J−｜jm＞|＝ 　(j＋m)(j−m＋1) h｜j (m-1)＞

であること [#] を思い出せば，³Φ₁ に J_- を作用させれば，三重項状態のすべての状態が得られるはずです。

先ず，｜jm＞表示では，

J−｜1 1＞|＝

2

h｜1 0＞

一方，J_- をスレーター行列式 ³Φ₁＝｜φ_a⁺φ_b⁺｜に作用させたときは，

J₋ ³Φ₁ 　＝J₋｜φ_a⁺φ_b⁺｜
　　　　　　　　＝h｜φ_a^-φ_b⁺｜＋h｜φ_a⁺φ_b^-｜　　　　

これら２つの式を比較して，　(　｜1 0＞ 〜 ³Φ₁　)

3Φ0 ＝ 1 2 (｜φa-φb+｜＋｜φa+φb-｜)

が分かります。さらに，J_- を作用させて，

J-3Φ0 ＝	h 2	(　｜φa-φb-｜＋｜φa-φb-｜)

一方，｜jm＞表示では，

J−｜1 0＞|＝

2

h｜1 -1＞

したがって，　　(　｜1 -1＞ 〜 ³Φ_-1　　)

3Φ-1 ＝｜φa-φb-｜

となります。

一重項

一方，２つの軌道に入っている電子スピンが上向きと下向きであるから　[#]，(　｜0 0＞＝¹Φ₀)

1Φ0＝ 1 2 ｛｜φa+φb-｜−｜φa-φb+｜｝

これらの式をスピン関数を分離して書くために，　

ここで，　³Φ₀，¹Φ₀　の右辺については，

｜φa+φb-｜＝	1 2	φa(r1)α1 φb(r1)β1 φa(r2)α2 φb(r2)β2	＝	1 2	[φa(r1)φb(r2)α1β2−φa(r2)φb(r1)α2β1]

｜φa-φb+｜＝	1 2	φa(r1)β1 φb(r1)α1 φa(r2)β2 φb(r2)α2	＝	1 2	[φa(r1)φb(r2)α2β1−φa(r2)φb(r1)α1β2]

この和もしくは差をとると，

｜φa+φb-｜＋｜φa-φb+｜＝	1 2	(φa(r1)φb(r2)−φa(r2)φb(r1))　(α1β2＋α2β1)

＝	1 2	φa(r1) φb(r1) φa(r2) φb(r2)	(α1β2＋α2β1)
＝	｜φaφb｜(α1β2＋α2β1)

｜φa+φb-｜−｜φa-φb+｜＝	1 2	(φa(r1)φb(r2)＋φa(r2)φb(r1))　(α1β2−α2β1)

＝	1 2	φa(r1) φb(r1) p φa(r2) φb(r2)	(α1β2−α2β1)
＝	|φaφb　|p(α1β2−α2β1)

これらを軌道関数とスピン関数を分離してまとめると，

3Φ1＝ ｜φaφb｜・α1α2 3Φ0＝ 1 2 ｜φaφb｜・(α1β2＋α2β1) 3Φ-1＝ ｜φaφb｜・β1β2 ３重項 1Φ0＝ 1 2 |φaφb|p (α1β2−α2β1) … １重項

または，

3Φ1＝ 1 2 φa(r1) φb(r1) φa(r2) φb(r2) α1α2 3Φ0＝ 1 2 φa(r1) φb(r1) φa(r2) φb(r2) ・ 1 2 α1 β1 p α2 β2 3Φ-1＝ 1 2 φa(r1) φb(r1) φa(r2) φb(r2) β1β2 ３重項 1Φ0＝ 1 2 φa(r1) φb(r1) p φa(r2) φb(r2) 1 2 α1 β1 α2 β2 １重項

とまとめられます。軌道関数部分が対称ならばスピン関数部分が反対称であり，軌道関数部分が反対称ならばスピン関数部分が対称となっていて，全波動関数が反対称となることで，フェルミ粒子系に対する波動関数の要件を満足させています。

２．一重項と三重項状態のエネルギー

２つの電子が中心力を受けている場合のハートリー近似による取り扱い。ハミルトニアンは，

H ＝ −

h

∇12 ＋∇22

＋

V(r 1)＋V(r 2))

＋

1

･

e2

2m

4πε0

r12

＝		h(r 1)＋h(r 2)		＋ g(r 1，r 2)　　･･･････　[*]

ただし，

h (r j )＝ −	h	∇j2　＋V(r j )    ；   j ＝ 1，2
	2m

g(r1，r2 )＝	e2	・	1
	4πε0		| r1 −r2 |

ハートリーフォック近似

j の位置座標 r_j ，スピン座標σ_j の両方を合わせた座標を τ_j と書くことにします。

解として，　スレーター行列式

Ψ(r1，r2 ) ＝｜ψaψb｜＝	1  2！		ψa(τ1)	ψb(τ1)
			ψa(τ2)	ψb(τ2)

の形をしているものの中で最適なものを探すことにします。　ここで，　　

ψ_m(τ_j)＝φ_m(r_j )χ(σ_j)　

です。

スレーター行列式では，ある一組の電子を互いに交換すると，全波動関数の符号が反転するようになっています。これは行列式が行の交換にたいして符号が反転することからすぐにわかります。

［２］　スレータ行列式で表される場合は，全エネルギーは，

＜H＞ ＝

Ψ*(τ1，τ2 ) H Ψ(τ1，τ2 )dτ1dτ2

＝　＜a|h|a＞＋＜b|h|b＞＋＜ab|g|ab＞ −＜ab|g|ba＞

２つのスレーター行列式で演算子を挟んで積分するとき(＜Ψ｜H｜Ψ＞などを計算するするとき)は， 一方を変数を固定した1つの項(どれでもよい)だけをとり，他方だけをスレータ行列を用いて， さらに係数√n！を１として積分をおこなっても同じ結果を得る。小出昭一郎(p235) 理由 N=2の場合で考えると，2！＝2より，6つの固有関数の積，A＝φχ，B＝χφとして，次の展開を考える。 (A−B)H(A−B)＝AH(A−B)＋BH(B−A)　　　　←間に入るHは省略 この各項は，φ，χの並びを一つ選んで(第１項ならば，φχ)と，それを反対称化した関数(φχ−χφ)と積の形をしており形をしており， 上の計算ではそのような項が，2！個現れることが分かります。ところが，最初に選ぶ並び，つまり，最初にどのように同種粒子に番号を振るか は系の微視的状態に違いは与えないので，上式右辺に現れる項はすべて等しいことが分かります。 これは任意のNについて言えます。

ここで，

＜ab|g|ab＞ ≡

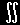ψa*(r1)ψb*(r2)g(r1，r2 )ψa(r1)ψb(r2)dr1dr2

［ クーロン積分 ］

＜ab|g|ba＞ ≡

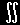ψa*(r1)ψb*(r2)g(r1，r2 )ψb(r1)ψa(r2)dr1dr2

［ 交換積分 ］

               

実際の計算　　

三重項のエネルギー

3Φ1＝｜φa+φb+｜＝		1 2	[φa(r1)φb(r2)−φa(r2)φb(r1)]α1α2

と[*]を用いて，ここではベタに計算してみる。

³E₁＝＜³Φ₁｜H｜³Φ₁＞

＝＜[φa*(r1)φb*(r2)−φa*(r2)φb*(r1)]α1α2｜		h(r 1)＋h(r 2)＋ g(r 1，r 2)				｜[φa(r1)φb(r2)−φa(r2)φb(r1)]α1α2＞

＝(1/2)｛＜φ_a^*(r₁)｜h(r ₁)｜φ_a(r₁)＞＜φ_b^*(r₂)｜φ_b(r₂)＞＜α₁｜α₁＞＜α₂｜α₂＞
　　　　　　　　　　　　　　＋＜φ_b^*(r₁)｜h(r ₁)｜φ_b(r₁)＞＜φ_a^*(r₂)｜φ_a(r₂)＞＜α₁｜α₁＞＜α₂｜α₂＞

　　　　＋＜φ_b^*(r₂)｜h(r ₂)｜φ_b(r₂)＞＜φ_a^*(r₁)｜φ_a(r₁)＞＜α₁｜α₁＞＜α₂｜α₂＞
　　　　　　　　　　　　　　＋　＜φ_a^*(r₂)｜h(r ₂)｜φ_a(r₂)＞＜φ_b^*(r₁)｜φ_b(r₁)＞＜α₁｜α₁＞＜α₂｜α₂＞

　　　　＋＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_a(r₁)φ_b(r₂)＞＜α₁｜α₁＞＜α₂｜α₂＞
　　　　　　　　　　　　　　＋＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_a(r₂)φ_b(r₁)＞＜α₁｜α₁＞＜α₂｜α₂＞

　　　　−＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_a(r₂)φ_b(r₁)＞＜α₁｜α₁＞＜α₂｜α₂＞
　　　　　　　　　　　　　　−＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_a(r₁)φ_b(r₂)＞＜α₁｜α₁＞＜α₂｜α₂＞　｝

＝(1/2)｛＜φ_a^*(r₁)｜h(r ₁)｜φ_a(r₁)＞＋＜φ_a^*(r₂)｜h(r ₂)｜φ_a(r₂)＞

　　　　＋＜φ_b^*(r₁)｜h(r ₁)｜φ_b(r₁)＞＋＜φ_b^*(r₂)｜h(r ₂)｜φ_b(r₂)＞

　　　　＋＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_a(r₁)φ_b(r₂)＞＋＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_a(r₂)φ_b(r₁)＞

　　　　−＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_b(r₁)φ_a(r₂)＞−＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_b(r₂)φ_a(r₁)＞｝

＝＜a|h|a＞＋＜b|h|b＞＋＜ab|g|ab＞ −＜ab|g|ba＞　　3重項のエネルギー

さらに，³E₀＝＜³Φ₀｜H｜³Φ₀＞，³E_-1＝＜³Φ_-1｜H｜³Φ_-1＞について計算しても同じ値が得られます。

一重項のエネルギー

¹E ＝ ＜¹Φ₀｜H｜¹Φ₀＞

＝＜[φa*(r1)φb*(r2)＋φa*(r2)φb*(r1)](α1β2−α2β1)｜		h(r 1)＋h(r 2)

＋ g(r 1，r 2)		｜[φa(r1)φb(r2)＋φa(r2)φb(r1)](α1β2−α2β1)＞

＝	1	｛＜φa*(r1)｜h(r 1)｜φa(r1)＞＜φb*(r2)｜φb(r2)＞＜α1β2−α2β1｜α1β2−α2β1＞
	4

　　　　　　　＋＜φ_b^*(r₁)｜h(r ₁)｜φ_b(r₁)＞＜φ_a^*(r₂)｜φ_a(r₂)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞
　　　　　　　　

　　　　＋＜φ_b^*(r₂)｜h(r ₂)｜φ_b(r₂)＞＜φ_a^*(r₁)｜φ_a(r₁)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞
　　　　＋＜φ_a^*(r₂)｜h(r ₂)｜φ_a(r₂)＞＜φ_b^*(r₁)｜φ_b(r₁)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞

　　　　＋＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_a(r₁)φ_b(r₂)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞
　　　　＋＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_a(r₂)φ_b(r₁)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞

　　　　＋＜φ_a^*(r₁)φ_b^*(r₂)｜g｜φ_a(r₂)φ_b(r₁)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞
　　　　＋＜φ_a^*(r₂)φ_b^*(r₁)｜g｜φ_a(r₁)φ_b(r₂)＞＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞　｝

   ↓  　＜α₁β₂−α₂β₁｜α₁β₂−α₂β₁＞＝2　を用いて

＝＜a|h|a＞＋＜b|h|b＞＋＜ab|g|ab＞ ＋＜ab|g|ba＞　　　１重項のエネルギー

結局，

¹E＝³E₁＋2＜ab|g|ba＞

これは1重項のエネルギーは，３重項より　２×交換積分＝2＜ab|g|ba＞　だけ高いことを示しています。

[目次]

H ＝ h(τ1 )＋h(τ2 )  ＋ g(τ1，τ2)

ただし，

h (r j )＝ −	h	∇j2　＋V(r j )    ；   j ＝ 1，2
	2m

g(r1，r2 )＝	e2	・	1
	4πε0		| r1 −r2 |

3Φ0＝｜φa+φb-｜＝	1 2	φa(r1)α1 φb(r1)β1 φa(r2)α2 φb(r2)β2	＝	1 2	[φa(r1)φb(r2)＋φa(r2)φb(r1)](α1β2−α2β1)

3Φ1＝	1 2	｜φaφb｜・α1α2