ときわ台学/摂動論/電磁場の量子化と電気双極子遷移

	電磁場の量子化と電気双極子遷移
f-denshi.com 更新日：07/03/15 　まだ加筆します。　分裂するかも

電気双極子放射の量子力学版です。（吸収も）

電子が光を吸収，または放出する過程を量子力学で記述することが目的です。
電磁場＋電子＋電子と電磁場の相互作用とに分けて考えます。

１．電磁場の量子化

［１］　電磁気学からベクトルポテンシャルとスカラーポテンシャルの定義を再掲すると，

E　＝－gradφ－ ∂A 　　　　　　　　　　　　　　　　　　　　　　　　　　（1）

∂t

B ＝ rot A 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（２）

div A ＋ ∂φ ＝ 0　［ローレンツ・ゲージ］　　　　　　　　　　　　（３）

c²∂t

これらは電荷も電流もない真空中では，

E　＝－ ∂A 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（1）’

∂t

B ＝ rot A 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（２）’
div A ＝0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（３）’

となります。また，アンペールの法則も思い出しておきましょう。

rotH　＝ ∂D 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（４）

∂t

さらに，真空中でD ＝ ε₀E，B ＝ μ₀H　であるから，

rotB　＝ε₀μ₀ ∂E 　　　　　　　　　　　　　　　　　　　　　　　　　　　（４）’

∂t

となります。この式に（１）’，（２）’を代入して，真空中の光速度cを用いれば，

∇²A－ ∂²A ＝0　　　　　　　　　　　　　　　　　　　　　　　　　　[*]　

c²∂t²

これは電磁場の方程式をベクトルポテンシャルで表したものです。

この波動方程式の一般解を周期境界条件（体積V＝L³）を満たす平面波解で，

A(r,t)＝ 1 ＝ { q_k(t)e^ik･r ＋ q_k^*(t)e^-ik･r }e　　　　　　　　　　　　（６）

V

と表します。ここで，e　はAの方向を向く単位ベクトル（電場の向きと同じ[#]）。

また，q_k(t)の一つの解は，

q_k(t)＝ |q_k| e^-iωt+δ

とおけますが，[*]　に代入すれば，

ω＝c|k|　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（７）

を満たしていることもわかります。

［２］　さて，Aは各kに対してそれと垂直な平面内にあるので，２つの基底ベクトルe_k_γとe_k_γ' の線形結合で表すことが可能で，結局，ベクトルポテンシャルの一般解を，

A(r,t)＝ 1 ＝ { q_k_γ(t)e^ik･r ＋ q_k_γ^*(t)e^-ik･r }e_k_γ

V

とおいて，q_k_γ(t)　を求めてやるとよいでしょう。古典場を量子場へ変換するときの定番です。フォノン場[#]も参考にしてください。

したがって，（１）’，（２）’へこれらを代入して，

E(r,t)＝ 1       ＝ iω_k{ q_k_{_γ}(t)e^ik･r － q_k_{_γ}^*(t)e^-ik･r }e_k_{_γ}　

  V

B(r,t)＝ 1       ＝ { q_k_{_γ}(t)e^ik･r － q_k_{_γ}^*(t)e^-ik･r } (k ×e_k_{_γ})

  V

一つ目の計算は時間で微分するだけなので，問題ないと思います。

SUSTAINABLE　TOKIWADAIGAK

［３］　一方で，電磁気学より真空中のエネルギー密度[#]は，

U＝ 1 ε₀E ･E＋μ₀^-1B ･B　

2

で与えられます。これに上のE(r,t) ，B(r,t) を代入すると，次のようにハミルトニアン密度が求まります。

H＝－ ε₀ (e_k_{_γ}･e_{k'_γ'})　ω_kω_k'＋c² (k ×e_k_{_γ}) ･(k' ×e_{k'_γ'})

2V

１番目の｛　　｝

　　　　　　・　 q_k_{_γ}q_{k'_γ'}e^+i(k+k')･r －q_k_{_γ}q_{k'_γ'}^*e^+i(k-k')･r －q_k_{_γ}^*q_{k'_γ'}e^-i(k-k')･r ＋q_k_{_γ}^*q_{k'_γ'}^*e^-i(k+k')･r 　　(12)

後ろの｛　　｝

かなり複雑な式ですが，電磁場が一様であるとき，この式の後ろの｛　　｝で，空間（r での）積分後に（４つある）指数関数が 0 とならないのは肩の部分が 0 のときだけ，つまり，
k＝±k'　となっているときだけ，H≠0　であることに注意すれば，そのようなケースだけを数えあげればよいことが分かります。　

その際，それぞれのkに対し，kに垂直な第1番目の基底が下に示すように，－kの一番目の基底と同一であるように定めておけば，計算が簡単になります。

実際，k '＝－k　のとき，(12)の１番目の｛　｝の各基底のベクトルの内積の計算値を表にしてみると，

(γ,γ’) |
|
|
|
|
| (1,1) (1,2) (2,1) (2,2)

(e_k_{_γ}･e_{-k_γ'})ω_k² ω_k² 0 0 -ω_k²

c²(k ×e_k_{_γ}) ･(-k×e_{-k_γ'}) -c²k² 0 0 c²k²

q_k_{_γ}q_{k'_γ'}の項和

これより，(12)の１番目の｛　｝は，（７）式　ω＝c|k|　を考慮すると，どの場合も 0 であることが分かります。そして式全体も 0 です。

さらに，k '＝k　のとき，(12)の１番目の｛　｝の各基底に対するベクトルの内積の計算値を表にしてみると，

(γ,γ’) |
|
|
|
| (1,1) (1,2) (2,1) (2,2)

(e_k_{_γ}･e_{k_γ'})ω_k² ω_k² 0 0 ω_k²

c²(k ×e_k_{_γ}) ･(k×e_{k_γ'}) c²k² 0 0 c²k²

q_k_{_γ}q_{k'_γ'}の項和－q_k_₁q_k₁^*－q_k_₁^*q_k₁ －q_k_₂q_k₂^*－q_k_₂^*q_k₂

この表から，(γ,γ’)＝(1,1)，(2,2)　の場合に積分は0とならず，1番目の｛　｝　は，－(ω_k²＋c²k²) となることがわかります。

よって，積分値は，

H＝ H dV＝ ε₀ (ω_k²＋c²k²)(q_k_{_γ}^*q_{k_γ}＋q_k_{_γ}q_{k_γ}^*)

2

H＝ 2ε₀ω_k²q_k_{_γ}^*q_{k_γ}　　　　　　　　　　　　　　　　　　　　　　　　　　(13)

［４］　次に（一般化）座標[#]を，

Q_k_{_γ}(t)　≡q_k_{_γ}(t)＋q_k^*(t)　（　＝2｜q_{k_γ}｜cos（ω_kt＋δ_{k_γ}）　）

で導入します。(13)をこの座標で置き換えたいのですが，この式を t で1，２回微分した式を用いて組み合わせると，

1 ( Q’_k_{_γ}(t)＋ω_k²Q_k_{_γ}(t)² ）　＝　2ω_k²q_k_{_γ}^*q_{k_j}

2

を満たしていることを示せます [#]。つまり，電磁場の全エネルギーは，

H＝ ε₀ (Q’_k_{_γ}(t)＋ω_k²Q_k_{_γ}(t)²）

2

⇔

m (x’(t)＋ω²x(t)²）

2

調和振動子の全エネルギー

と表記できることが分かります。これを調和振動子のハミルトニアンと見比べて，ε₀ と m とを対応させれば，

「電磁場は，無限個の1次元調和振動子の集まりと同等である。」ということができます。（Jeansの定理）

［５］　一般化運動量は，一般化座標から

P_k_{_γ}≡ε₀Q’_k_{_γ}　＝ε₀ d Q_k_{_γ}(t)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

dt

となります。量子論へは，

P_k_{_γ}　　⇒　　－ih ∂ 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

∂Q_k_{_γ}

と置き換えればよいだけでしたね[#]。

H＝－ h ∂ ＋ ε₀ ω_k²Q_k_{_γ}(t)²）

2ε₀ ∂Q_k_{_γ} 2

電磁場の量子力学的ハミルトニアンは，調和振動子のそれと全く形式が同じ[#]なので，そっくりコピーして数表示（占有数表示）へ移行させても問題ないでしょう。結果をまとめると，

消滅・生成演算子

E_n　＝ h ω_k(n_k_{_γ}＋1/2)

消滅演算子：　a_k_{_γ}　⇔

ε₀ω_k

2h

Q_k_{_γ}＋ iP_k_{_γ} 　　＝

2ε₀ω_k

h

q_k_{_γ}

ε₀ω_k

生成演算子： a^*_k_{_γ}⇔

ε₀ω_k

2h

Q_k_{_γ}－ iP_k_{_γ} 　　　＝

2ε₀ω_k

h

q_k_{_γ}^*

ε₀ω_k

　　q_k_{_γ}　　　　⇔　　　　

h

2ε₀ω_k

a_k_{_γ}　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　q_k_{_γ}^*　　　⇔　　　　

h

2ε₀ω_k

a^*_k_{_γ} 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

上式は調和振動子のときと同形式なのですが，電磁場の場合は，様々な波数kに対応して無限個の調和振動子を考える必要があります。

したがって，個数ケットも波数kに対応して，以下のように記述する必要があります。

消滅－生成演算子の性質

　a_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝ n_k_{_γ} ｜n₁，n₂，･･･，n_k_{_γ}－1，･･･＞　　　

　a^*_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝　 1＋n_k_{_γ} ｜n₁，n₂，･･･，n_k＋1，･･･＞

生成演算子の定義

a^*_k_{_γ}a_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝n_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞

a_k_{_γ}a^*_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝(n_k_{_γ}＋1)｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　

ここで，n_k_{_γ}は波数ベクトルk　で表される光子（フォトン）の数です。

共通するk_γに対する演算子ては，次の交換関係が存在することは自明でしょう。

a_k_{_γ}a^*_k_{_γ}－a^*_k_{_γ}a_k_{_γ}　＝1　　　（交換関係）

これらの関係式は場の量子化の一般論で[#]述べたとおりです。

結局，消滅演算子を用いて，　q_k_{_γ}，q_k_{_γ}^*をa_k_{_γ}，a^*_k_{_γ}に置き換えると，ベクトルポテンシャル等は次のようになります。

電磁場の生成消滅演算子による表現

H＝ hω_ka^*_k_{_γ}a_k_{_γ}　

A(r,t)＝

h

2ε₀V

1 ＝{ e^ik･r a_k_{_γ}＋ e^-ik･r a^*_k_{_γ}}e_k_γ

ω_k

E(r,t)＝

h

2ε₀V

i

ω_k

{ e^ik･r a_k_{_γ}－ e^-ik･r a^*_k_{_γ}}e_k_{_γ}

B(r,t)＝

h

2ε₀V

i ＝ { e^ik･r a_k_{_γ}－ e^-ik･r a^*_k_{_γ}} (k ×e_k_{_γ} ) 　　　　　　

ω_k

［６］　シュレーディンガー場で述べた[#]ように時間依存性を演算子に含ませたハイゼンベルグ表示に対応させるためには，

ハイゼンベルグ表示へ変更

a_k_{_γ}(t)＝exp（－iω_kt）a_k_{_γ}

a^*_k_{_γ}(t)＝exp（iω_kt)a^*_k_{_γ}

とします。

最後に運動量です。電磁気学の運動量密度はポインティングベクトルをc²で除した次式与えられ[#]ますが，

G　≡ (E ×H )/c²＝　 1 (E ×B )

c²μ₀

これに生成-消滅演算子で表したE と B を代入して，

G dV　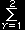＝ hk a^*_k_{_γ}a_k_{_γ}

が得られます。これも代入するだけで難しくないので各自確認してください。計算方法はこちら　⇒　[#]

SUSTAINABLE　TOKIWADAIGAK

非定常状態の摂動論　から抜粋して補足　（最後の結果だけ受け入れて先へ進んでも構いません。）

摂動のあるシュレーデインガー方程式を

ih ∂ ψ(r,t) ＝ Hψ(r,t)　　　　　　　　　　　　　　　　　　　　(a-1)

∂t

H＝H₀＋H’　　　

H’は摂動で，H₀ に関しては完全に解が分かっていて，

H₀φn＝E_nφ_n(t)　　　　　　　：　　φ_nは完全系とする。

ih ∂ ψ₀(r,t) ＝ H₀ψ₀(r,t)

∂t

ψ₀(r,t) ＝ c_nexp(-iE_nt/h)φ_n

と書くことができるとします。

摂動がある場合の波動関数は，H’→0　で上の式に帰着することを念頭におけば，c_n→c_n(t)　とおくことで，

ψ(r,t) ＝ c_n(t)exp(-iE_nt/h)φ_n　　　　　　　　　　　　　　　　　　　　　　　　　(a-4)

と追加の摂動による時間依存性をc(t)に含めることにしましょう。このとき，時刻 0 の始状態φ_i　では，

c_i(0)＝1　，　　c_n≠i(0)＝0

となります。

さて，(4)を(1)に代入して，左からφ^*_f をかけて積分すると，

ih　exp - iE_ｆt d c_f(t)＝ c_n(t)exp - iE_nt <f |H’| n>　　　(a-6)　

h dt h

ここで，右辺について，時間が十分短く，　　t　<<　

c_i(0)≒1　　　c_n≠i(0)≒0

の状況を考えます。

f≠i　であるとき，(6)式は，近似によって，

ih　exp - iE_ｆt dc_f(t) )＝exp - iE_it <f |H’| i>

h dt h

このtに関する1次微分方程式は簡単に解けて，

c_f(t)＝ 1－exp( i (E_ｆ－E_i)t/h) <f |H’| i>　　　　　　　 (a-9)

E_ｆ－E_i

f＝i　の場合は，

ih　 dc_i(t) )＝c_i(t)<i |H’| i>

dt

を解いて，

初期状態のままでいるときの係数の変化

　　　 c_i(t)＝exp ( －i <i |H’| i> t/h )　　　　　←　位相だけが変化する

となります。

したがって，時間tの後に状態 i から f に遷移が起こっている確率は(9)とその複素共役とを乗じて，

　｜c_f(t) |²＝ 2－2cos( (E_ｆ－E_i)t/h) ｜<f |H’| i> |²＝ 4sin²(ω_i→ft/2) ｜<f |H’| i> |²

(E_ｆ－E_i)² (hω_i→f)²

時刻ｔ後の遷移確率

｜c_f(t) |²＝ 4sin²(ω_i→ft/2) ｜<f |H’| i> |²

(hω_i→f)²

ただし，

ω_i→f＝ E_ｆ－E_i

h

という記号を導入しました。

｜c_f(t) |² の振動する部分（分数のところ）は，ω_i→f＝0　に鋭いピークを持つ関数でることが分かります。　

E_i　＝E_a＋n₁hω₁＋n₂hω₂＋　･･･　＋　n_k_{_γ}　hω_k　　　･･･

E_ｆ　＝E_b＋n₁hω₁＋n₂hω₂＋　･･･　＋(n_k＋1)hω_k　　　････

SUSTAINABLE　TOKIWADAIGAK

３．電気双極子遷移

［１］　光の吸収-放出の演算子　　　（注意：電子の電荷の符号は－e として記述する。）

準備は整いましたので，電子が電磁波を吸収して高エネルギーにジャンプしたり，
その逆に電子が電磁波を放出して低エネルギーへ遷移する様子を量子力学的に記述する方法を示しましょう。

まず，ハミルトニアンです。

電磁場のハミルトニアン

H_ph　＝ hω_ka^*_k_{_γ}a_k_{_γ}　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（3-1）　

電子系のハミルトニアン（電磁場がないとき）

H_el　＝ 1 p_j²＋V(r₁,　r₂,　･･･　,r_N, t)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

2m

電子系のハミルトニアン（電磁場があるとき，電子の運動量にベクトルポテンシャルの項が付加される{#}）

H_el’　＝ 1 { p_j＋e A(r_j) }²＋V(r₁,　r₂,　･･･　,r_N, t)　　　　　　　　　　　　　　　　　　　　　　　　　　

2m

したがって，電子相互作用ハミルトニアン（＝電場あるとき－電場ないとき）は，

H’＝H_el’－H_el　

　　＝ 1 e p_j･A(r_j)　　　　　　　　　　＋eA(r_j)･p_j＋e²A(r_j) ²

2m

　　＝ 1 -ih｛ e∇_jA(r_j)＋eA(r_j)･∇_j ｝＋eA(r_j)･p_j＋e²A(r_j) ²

2m

　　　　　　　↓divA ＝ 0 より

　　＝ e A(r_j)･p_j　＋ e² A(r_j) ² 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(3-6)

m 2m

１次の項　 H₁ ２次の項

ここで，１次の項はここで説明する電気双極子遷移に関する項で，２次の項は電気四重極子と磁気双極子遷移が関わる項です。

ここで，A(r_j) を生成・消滅演算子

A(r,t)＝

h

2ε₀V

1 ＝{ e^ik･r a_k_{_γ}＋ e^-ik･r a^*_k_{_γ}}e_k_γ

ω_k

で表し，２次の項を落とせば，（２次の項は物質の磁気的性質ところで説明しています。）

H₁ ＝ e

h

2ε₀V

1 {　e^ik･r_^j (e_k_{_γ}・p_j) a_k_{_γ}＋ e^-ik･r_^j (e_k_γ・p_j) a^*_k_{_γ}}

m

ω_k

［２］　光の吸収-放出の遷移確率

時間に関する摂動論から遷移確率は，

｜c_f(t) |²＝ 4sin²(ω_i→ft/2) ｜<f |H’| i> |²　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(3-9)

(hω_i→f)²

を計算すればよいことが分かっています。摂動として，「光と電子との相互作用」　を考えるときはこのH’のところへ先に計算したH’＝H_el’－H_el　を適用すればよいわけです。ただし，ここでは，１次の項だけを考慮して（H₂以下は無視）　次式，

H’～H₁ ＝ e

h

2ε₀V

1 {　e^ik･r_^j (e_k_{_γ}・p_j) a_k_{_γ}＋ e^-ik･r_^j (e_k_γ・p_j) a^*_k_{_γ}}　　　　

m

ω_k

を摂動のハミルトニアンと考えます。

一方，固有関数の変化は電子状態と電磁場との積で記述できます。（演算子が和であるときは対応するケット（波動関数）は（テンソル）積で表される。[#] ）

始状態

｜i >＝｜a>｜n₁,n_2,･･･,n_γ,　･･･>　　　　　⇔　｜a>｜n_γ>　と略記

終状態

｜f >＝｜b>｜n₁,n₂,･･･,n_γ±1,　･･･>　　　⇔　｜b>｜n_γ±1>　と略記

光の吸収　＝　光子が消滅（マイナス符号）
光の放出　＝　光子が生成（　プラス符号）

また，

ω_i→f＝ E_ｆ－E_i

h

において，

E_i　＝E_a＋n₁hω₁＋n₂hω₂＋　･･･　＋　n_k_{_γ}　hω_k＋　　･･･
E_ｆ　＝E_b＋n₁hω₁＋n₂hω₂＋　･･･　＋(n_k±1)hω_k＋　　････
E_f－E_i＝E_b－E_a±hω_k

と考えます。

期待値の２乗の計算は，

光の吸収の場合は　H₁　は光の消滅を表す第１項だけが寄与（ゼロとならない）し，

<f｜H₁｜i > ＝ e

h

2ε₀V

1 < b｜e^-ik･r_^j (e_k_{_γ}・p_j) ｜a > <n_γ-1｜a_k_{_γ}｜n_γ>

m

ω_k

光の放出の場合は，　H₁　は光の消滅を表す第２項だけが寄与し，

<f｜H₁｜i > ＝ e

h

2ε₀V

1 < b｜e^-ik･r_^j (e_k_{_γ}・p_j) ｜a > <n_γ+1｜a^*_k_{_γ}｜n_γ>

m

ω_k

となります。ここで，これらの式から，

　a_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝ n_k_{_γ} ｜n₁，n₂，･･･，n_k_{_γ}－1，･･･＞　　　

　a^*_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝　 1＋n_k_{_γ} ｜n₁，n₂，･･･，n_k＋1，･･･＞

であることを思い出せば，｜＜|　|＞｜² の項からそれぞれ　n_k_{_γ}，n_k_{_γ}＋1　がでてきます。すなわち，

|<f｜H₁｜i >|² ＝　n_k_{_γ}　　 e

h

2ε₀V

1 < b｜e^-ik･r_^j (e_k_{_γ}・p_j) ｜a > <n_γ-1｜a_k_{_γ}｜n_γ> ²

m

ω_k

|<f｜H₁｜i >^|2 ＝（n_k_{_γ}＋1) e

h

2ε₀V

1 < b｜e^-ik･r_^j (e_k_{_γ}・p_j) ｜a > <n_γ+1｜a^*_k_{_γ}｜n_γ> ²

m

ω_k

吸収確率　　∝　　　n_k_{_γ}
放出確率　　∝　　　n_k_{_γ}＋1

であることが分かります。

放出確率が　（n_k＋1）　に比例するため，n_k＝0　のときであっても光の放出が起こります。この寄与による光の放出を自然放出といいます。
一方，該当する光子の個数 n_k_{_γ}に比例する光の吸収，放出を誘導吸収，誘導放出といいます。

［３］　に電磁波がk-空間に連続的に分布するとして，その微小範囲を

dk＝　k²dkdΩ　（＝k²sinθdθdφ）　（dΩは立体角の微分量）

とします。また，空間Vに対応するk-空間のkの数密度は，V/(2π)³でした[#]。したがって，

k＝ω_k/c，
dk＝dω_k/c

なる関係も用いて，角振動数がω_k　とω_k＋dω_k　の間にあり，方向がdΩの範囲を向いている光の状態数は，

Vω_k² dω_kdΩ

8πc³

と書き表すことができます。これに f への遷移確率｜c_f(t) |² 乗じた，

V ･ 4sin²(ω_i→ft/2) ω_k²｜<f |H’| i> |²　dω_kdΩ

8πc³ (hω_i→f)²

　　ただし，　　　　　　ρ(ω_k)＝ Vω_k²

8π³c³

を考えると，これは

最初に状態 i にあった電子が角振動数がω_kとω_k＋dω_kの間にあり，
方向がdΩの中にあるような光を放出・吸収して，t 秒後に状態 f になる確率

を示しています。

さらにω_kについて積分をすると，あらゆる波長との相互作用を考慮した式となるはずです，時間に関する遷移確率は，ω_i→f＝0　，すなわち，　　　　　　　　　

ω_k＝ω_ba≡ E_b－E_a

h

のごく近傍にだけに鋭いピークを持つ関数でることが分かります。　この範囲で，ω_ba²｜<f |H’| i> |²　を平均値として積分の外に出す近似を行えば，

Vω_ba² ｜<f |H’| i> |²dΩ 4sin²(ω_i→ft/2) ² dω_k

8πc³ (hω_i→f)²

また，dω_i→＝±dω_k　，積分公式：　　（sinx / x）²dx＝π　であることを用いれば，

＝ Vω_ba² ｜<f |H’| i> |²dΩ 2π t

8πc³ h²

ここで，<f |H’| i> として，<f｜H₁｜i > を用いれば，

単位時間当たり（　t > >2π/ω_k　のとき）

吸収：　　 ω_ba 　　<n_k_{_γ}>　｜<b｜ e e^-ik･r_^j (e_k_{_γ}・p_j) ｜a >｜²dΩ

8π²hc³ε₀ m

放出：　 ω_ba (<n_k_{_γ}>＋1)｜<b｜ e e^ik･r_^j (e_k_{_γ}・p_j) ｜a >｜²dΩ

8π²hc³ε₀ m

ここで，

ω_ba＝｜E_b－E_a｜

h

<n_k_{_γ}>：平均値

［４］　いわゆる双極子遷移（放射・吸収）の量子論に基づく遷移確率を求めるのに必要な作業は，

<b｜ e e^-ik･r_^j (e_k_{_γ}・p_j) ｜a >｜² 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

m

の見積もりを行うだけです。

この積分も厳密解を求めることはできませんので，次の条件下で近似を用います。

光の波長　（λ～1/｜k｜　>>　原子サイズ　　（｜r｜）

すなわち，｜k ･r｜<< 1　なので，かなり大胆に指数部を　１　と近似します。

< b｜e e^-ik･r_^j (e_k_{_γ}・p_j/m) ｜a >≒< b｜e (e_k_{_γ}・p_j/m) ｜a >

ここで，公式，（ｊは電子に振られた番号）

[H，r_j]　＝－ ih p_j

m

を利用すると，

< b｜e (e_k_{_γ}・p_j/m) ｜a >＝ i < b｜ e (e_k_{_γ}・[Hr_j－ｒ_jH] ) ｜a >

h

　　　　　　　　　　　　　　　＝ i < b｜ e (e_k_{_γ}・[E_br_j－r_jE_a] )｜a >

h

　　　　　　　　　　　　　　　＝ i ・[E_b－E_a] < b｜ (e_k_{_γ}・e r_j] ) ｜a >

h

ここで，

P ≡－e ｒ

を電気双極子と定義すれば，

<b｜ e e^-ik･r_^j (e_k_{_γ}・p_j) ｜a >＝　－ i ・[E_b－E_a] < b｜ (e_k_{_γ}・ P) ｜a >

m h

を得ます。このPに関する積分値が電磁波の吸収･放出強度を決めていることが分かりました。

以上すべての係数も揃えて結果を書き下ろすと，次のとおりです。

電気双極子遷移確率　

　単位時間当たり　　　（　t > >2π/ω_k　のとき）

吸収：　　 ω₀³ <n_k_{_γ}> |< b｜ (e_k_{_γ}・ P) ｜a >|² dΩ

8π²hc³ε₀

放出：　 ω₀³ (<n_k_{_γ}>＋1) <| b｜ (e_k_{_γ}・ P) ｜a >|² dΩ

8π²hc³ε₀

ここで，

ω₀＝｜E_b－E_a｜

h

<n_k_{_γ}>：平均値

全方位にわたるときは，dΩ　→　4πとすればよい。

[目次へ]

SUSTAINABLE　TOKIWADAIGAK

ラグランジュ形式による説明

場の理論から

∂L

－

∂

∂L

－

∂

∂L

－

∂

∂L

－

∂

∂L

　＝　0　　

ラグランジュ（密度）方程式
［運動方程式と等価になるよう定める］

∂ψ

∂t

∂	∂ψ

	∂t

∂x

∂	∂ψ

	∂x

∂y

∂	∂ψ

	∂y

∂z

∂	∂ψ

	∂z

↓ L を決定

πⁱ≡	∂L	運動量（密度）

	∂A_i’

↓　πⁱ　から

H　＝　πⁱA’_i　-L　　　ハミルトニアン

∂_μ	∂L	－	∂L	＝　0	電磁場のラグランジュ方程式

	∂(∂_μAⁱ)		∂Aⁱ

∂_μ	∂L	－	∂L	＝　0	電磁場のラグランジュ方程式

	∂(∂_μφ)		∂φ

電磁場テンソルによる記述

F_ij ＝	∂A_j	－	∂A_i	＝∂_iA_j－∂_jA_i　　　　；　　F^ij　＝∂ⁱA^j－∂^jAⁱ

	∂xⁱ		∂x^j

マクスウェル方程式（ローレンツゲージ）

∂F^ik	＝μ₀jⁱ

∂x^k

－

マクスウェル場

方程式

∂_ν	∂L	－	∂L	＝　0

	∂(∂_νA^μ)		∂A^μ

∂_νF^μν＝μ₀j^μ

□ A －∂^μ(∂_νA^ν)＝（　0　）

－	1	F^μνF_μν　＋j_μA^μ

	4μ₀

－	1	(∂^μA^ν∂_μA_ν－∂^μA^ν∂_νA_μ)＋j_μA^μ＝　0

	2μ₀

－	1	F^μνF_μν　＝	ε	E²＋	μ	H²

	4μ₀		2		2

π⁰＝－（1/μ₀）∂_μA^μ，　
πⁱ＝－(1/μ₀)∂ⁱA⁰－A’ⁱ　　　　　i=1,2,3

－	1	π^μπ_μ＋	1	∂_iA_μ∂ⁱA^μ

	2		2μ₀

一般化座標　Q

一般化運動量　π

-----------------------------------------------------------------------------------

古典-粒子　　　（電荷をq とする）

-------------------------------------------------------------------------------

力学的運動量　　 Π　＝p－eA

ゲージ固定項

自然単位系

E　＝－gradφ－	∂A	（1）

	∂t

div A ＋	∂φ	＝ 0　［ローレンツ・ゲージ］　　　　　　　　　　　　（３）

	c²∂t

E　＝－	∂A	（1）’

	∂t

rotH　＝	∂D	（４）

	∂t

rotB　＝ε₀μ₀	∂E	（４）’

	∂t

H＝－	ε₀	(e_k_{_γ}･e_{k'_γ'})　ω_kω*_k'*＋c² (k ×e_k_{_γ}) ･(k' ×e_{k'_γ'})

	2V
		１番目の｛　　｝

・		q_k_{_γ}q_{k'_γ'}e^+i(k+k')･r －q_k_{_γ}q_{k'_γ'}^e^+i(k-k')･r －q_k_{_γ}^q_{k'_γ'}e^-i(k-k')･r ＋q_k_{_γ}^q_{k'_γ'}^e^-i(k+k')･r		(12)
		後ろの｛　　｝

(γ,γ’)	\| \| \| \| \| \|	(1,1)	(1,2)	(2,1)	(2,2)

(*e_k*_{_γ}･e_{-k_γ'})ω_k²		ω_k²	0	0	-ω_k²
c²(k ×*e_k*_{_γ}) ･(-k×e_{-k_γ'})		-c²k²	0	0	c²k²
q_k_{_γ}q_{k'_γ'}の項和

(γ,γ’)	\| \| \| \| \|	(1,1)	(1,2)	(2,1)	(2,2)

(*e_k*_{_γ}･e_{k_γ'})ω_k²		ω_k²	0	0	ω_k²
c²(k ×*e_k*_{_γ}) ･(k×e_{k_γ'})		c²k²	0	0	c²k²
q_k_{_γ}q_{k'_γ'}の項和		－q_k_₁q_k₁^－q_k_₁^q_k₁			－q_k_₂q_k₂^－q_k_₂^q_k₂

H＝	H dV＝	ε₀	(ω_k²＋c²k²)(q_k_{_γ}^q_{k_γ}＋q_k_{_γ}q_{k_γ}^)

		2

1	( Q’_k_{_γ}(t)＋ω_k²Q_k_{_γ}(t)² ）　＝　2ω_k²q_k_{_γ}^*q_{k_j}

2

P_k_{_γ}≡ε₀Q’_k_{_γ}　＝ε₀	d	Q_k_{_γ}(t)

	dt

P_k_{_γ}　　⇒　　－ih	∂

	∂Q_k_{_γ}


a_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝		n_k_{_γ}	｜n₁，n₂，･･･，n_k_{_γ}－1，･･･＞


a^*_k_{_γ}｜n₁，n₂，･･･，n_k_{_γ}，･･･＞　＝		1＋n_k_{_γ}	｜n₁，n₂，･･･，n_k＋1，･･･＞

ih	∂	ψ(r,t) ＝ Hψ(r,t)　　　　　　　　　　　　　　　　　　　　(a-1)

	∂t

c_f(t)＝	1－exp( i (E_ｆ－E_i)t/h)	<f \|H’\| i>　　　　　　　 (a-9)

	E_ｆ－E_i

｜c_f(t) \|²＝	2－2cos( (E_ｆ－E_i)t/h)	｜<f \|H’\| i> \|²＝	4sin²(ω_i→ft/2)	｜<f \|H’\| i> \|²

	(E_ｆ－E_i)²		(hω_i→f)²

H_el　＝	1	p_j²＋V(r₁,　r₂,　･･･　,r_N, t)

	2m

H_el’　＝	1	{ p_j＋e A(r_j) }²＋V(r₁,　r₂,　･･･　,r_N, t)

	2m

＝	1	e p_j･A(r_j)　　　　　　　　　　＋eA(r_j)･p_j＋e²A(r_j) ²

	2m

＝	1	-ih｛ e∇_jA(r_j)＋eA(r_j)･∇_j ｝＋eA(r_j)･p_j＋e²A(r_j) ²

	2m

＝		e	A(r_j)･p_j	＋		e²	A(r_j) ²	(3-6)

		m				2m
	１次の項　 H₁				２次の項

｜c_f(t) \|²＝	4sin²(ω_i→ft/2)	｜<f \|H’\| i> \|²　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　(3-9)

	(hω_i→f)²

V	･	4sin²(ω_i→ft/2)	ω_k²｜<f \|H’\| i> \|²　dω_kdΩ

8πc³		(hω_i→f)²

ただし，　　　　　　ρ(ω_k)＝	Vω_k²

	8π³c³

Vω_ba²	｜<f \|H’\| i> \|²dΩ	4sin²(ω_i→ft/2)	²	dω_k

8πc³		(hω_i→f)²

<b｜	e	e^-ik･r_^j (*e_k*_{_γ}・p_j) ｜a >｜²

	m

< b｜e	(*e_k*_{_γ}・p_j/m) ｜a >＝	i	< b｜	e (*e_k*_{_γ}・[Hr_j－ｒ_jH] ) ｜a >

		h

＝	i	< b｜	e (*e_k*_{_γ}・[E_br_j－r_jE_a] )｜a >

	h