| 303 結晶格子 | |
| f-denshi.com 更新日: | |
| サイト検索 | |
[1] 結晶の大きさは原子の大きさに比べて無限に大きいとして考えます。つまり、原子配列は規則的に無限に続いているとみなすのです。
まず、結晶の任意の一点 r を r’へ移動させる平行移動(並進操作):
r’ = r + n1a+n2b+n3c ( n1、n2、n3は整数 )
によって、原子配列が実質的に変化しないとき、この3つのベクトルa、b、c を単位格子ベクトル、これらベクトルの作る平行六面体(2次元の場合は平行四辺形)を結晶の単位格子、または単位胞と言います。 また、
n1a+n2b+n3c (n1、n2、n3 は整数)
で表される空間の点を格子点、その配列を結晶格子、または空間格子と呼びます。そして、単位構造とは、それを格子点上に並べると全空間を埋め尽くし、かつ結晶をあらわせるような原子の配列を言います。すなわち、
単位格子 + 単位構造 ⇒ 結晶構造 ( Crystal )
という関係で表せます。
[2] この関係を具体的な例で説明しましょう。(2次元結晶で)
** 基本単位格子 単位格子 A、A’、B、C ○ ○ D × ○ E × ×
平行四辺形、A、B、C はどれも内部に3個分の原子を含む単位格子で平行四辺形の各頂点は格子点とすることができます。また、その平行四辺形内部の原子配置は各単位格子に対応する単位構造とすることができます。このように単位格子の取り方は一意的ではありません。
平行四辺形 D は6個の原子を含む単位格子で、D を隙間なく空間にならべて結晶構造を構成することができます。A、B、C
のように面積 (3次元の場合は体積 ) が最小の単位格子を基本単位格子と呼びます。また,基本単位格子を与えるような単位格子ベクトルは基本並進ベクトル(または基本単位格子ベクトル)と呼ばれます。
平行四辺形 E は平行四辺形、A、B、C と同じ面積をもち、幾何学的には全空間を埋め尽くすはできます。しかし、その格子点にどんな基本構造を並べても結晶構造を構成できないので単位格子ではありません。
単位胞(Unit Cell)&Bravais Lattice)=14種類
[3] ブラベー は3次元の結晶構造を7つの結晶系、さらに14種類の結晶格子 ( =ブラベー格子) に分類しました。
| 結晶系 | 格子軸の特徴 | 対称性 (右図の左から順に) |
ブラベ単位格子 | ||
| 三斜晶系 Triclinic |
a≠b≠c α≠β≠γ 単純 |
単純格子 | 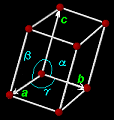 |
||
| 単斜晶系 Monoclinic |
a≠b≠c α=γ=90° β≠90° 単純+底心 |
単純格子 底心格子 |
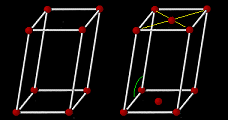 |
||
| 斜方晶系 Orthorhombic |
a≠b≠c α=β=γ=90° 単純+底心 +面心+体心 |
単純格子 体心格子 底心格子 面心格子 |
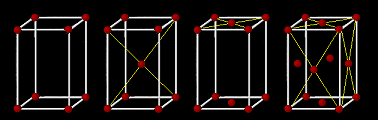 |
||
| 正方晶系 Tetragonal |
a=b≠c α=β=γ=90° 単純+体心 |
単純格子 体心格子 |
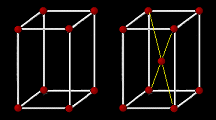 |
||
| 六方晶系 Hexagonal |
a=b≠c α=β=90° γ=120° 単純 |
単純格子 | 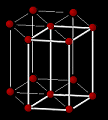 |
||
| 三方晶系 (菱面体晶系) Rhombohedral (Trigonal) |
a=b=c α=β=γ<120°≠90° 単純 |
単純格子 | 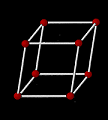 |
||
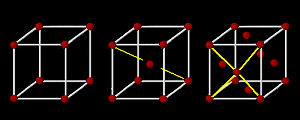
| 立方晶系 Cubic |
a=b=c α=β=γ=90° 単純+体心+面心 |
単純格子 体心格子 面心格子 |
 |
||
これはあまり説明は要らないと思います。
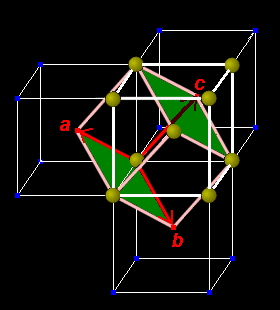
[4] よく使われる体心立方格子と面心立方格子の基本単位格子の取り方を下に図示しておきます。赤いベクトルが基本並進ベクトル、これとピンクで囲まれた平行六面体が基本単位格子です。
 |
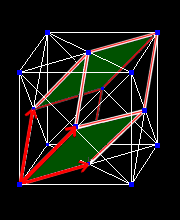 |
| 体心立方格子 | 面心立方格子 |
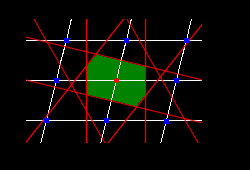
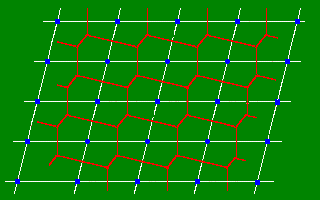
次の規則にしたがって得る。
1) ある格子点から隣接する格子点へ直線を引きます。
2) この直線を等分する垂直な面(垂直二等分面)を描きます。
3) 1)と2)を全ての方向で実行します。
 |
⇒ |  |