| ドルーデモデル | ||
| f-denshi.com 更新日: 21/09/27 | ||
| サイト検索 | ||
導電体(金属)と光の相互作用の古典的なモデルの説明です。
1.ドルーデモデル
金属内の自由電子の分散関係の方程式は,ローレンツモデル[#] において復元力が働かない,すなわち,運動方程式,
m d2x +mγj dx + mωj2x = eE0 exp(−iωt) [ ローレンツモデル ] dt2 dt
において,左辺の第3項を落とした,
m d2x +mγj dx = eE0 exp(−iωt) [ ドルーデモデル ] ・・・・・・ (1) dt2 dt
となります。すると,複素誘電関数はローレンツモデルにおける解[#] のうち,j = 1 について,f1 = 1,ω1 = 0, γ1 =γ として和をとり,
εr = 1− Ne2 ε0m*V(ω2+iγω)
= 1− ωp2 ω(ω+iγ)
= 1− ωp2 + i ・ ωp2 ω2 + 1/τ2 ωτ(ω2 + 1/τ2)
= 1− ( hωp)2+ i ・ ( hωp)2( hω)2 + (h/τ)2hω(τ/h)((hω)2+ (h/τ)2)
ドルーデ の式が得られます。ここで,
ωp =
Ne2 ε0m*V , 及び, τ=γ-1
とおきました。 ωp はプラズマ振動数,τ を平均自由時間(平均散乱時間)と言います。
ドルーデモデルにおける複素比誘電率の角周波数依存性を光子エネルギー(hω)依存性に換えてプロットすると,下図となります
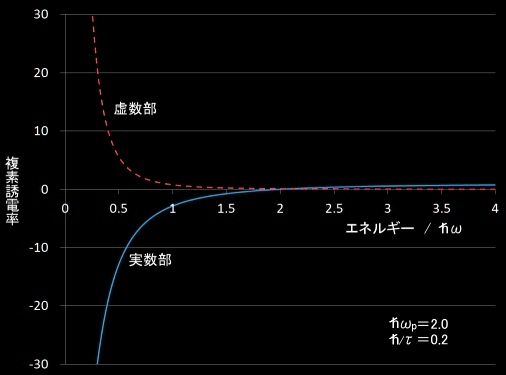
また,角周波数ω⇒0の極限では,
εr虚数部 = 1/ωτ → ∞ εr実数部
なので,
|εr| → ∞,
位相のずれ → π/2
となります。
一方,可視光領域では自由電子の平均自由時間τは光の振動の周期よりも長いことが知られているので,ω>>1/τ=γとみなすことができます(散乱を無視)。その場合は, ←その周波数に対応して,γが小さい(=吸収が起こりにくい)
εr = 1− ωp2 ω2
と近似できます。金属は光の振動数がプラズマ振動数より大きいか否かでその挙動が変化すると考えられます。すなわち,
光の振動数が ω>>ωp ならば,誘電率は実数となり,金属は光を透過させる。 ω<<ωp ならば,誘電率の実数部は負となり,金属中で光は減衰。 ⇔ 強い反射。
ということができます。ω<<ωp では 比誘電率の実数部は負であると屈折率は純虚数(実際は虚数部が大きい)とな り, 光は金属中を急速に減衰し,強い反射が起きると考えられます。しかし,実際の金属では,バンド間遷移などほかの要因によるエネルギー吸収が強く現れるため,可視部領域や紫外領域ではドルーデの式はあまり良く成り立ちません。
ローレンツモデルと比較
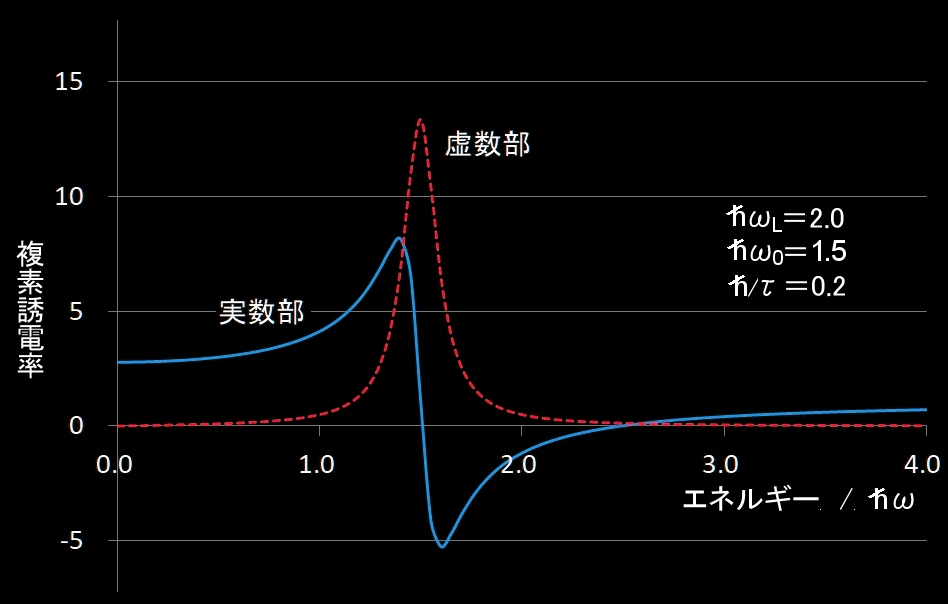
|
プラズモンとは, 古典的な説明 + α
光は空間を光速度で伝播する電磁場です。特にその電場成分に着目すれば,光照射されている金属粒子は振動する電場中に置かれている粒子と考えることができます。 金属粒子を静電場に置くと,金属内部の自由電子は力を受け移動して,金属内部に電場が生じないような分布ができたところで平衡に達します。つまり,金属内部に電場が形成されません。電気力線が金属内部に侵入できないと言うような言い方もします。電場が十分ゆっくり変化するときもこの事情は同じで,電場の変動に応じて金属内部の自由電子は常に金属粒子内に内部電場を形成しないように分布します。言い換えると,金属内部に, ところが,電子にも質量があり,その自由電子の分布形成には有限の時間がかかるため,振動数が非常に高いところでは,自由電子は金属内部の電場を常に打ち消すように十分な速さで動くことができず,ある程度の電場が金属内部に形成されるようになります。これは プラズマ振動数とは,光が不透過から透過へ変わる境目の振動数をいいます。その周波数近辺の光を金属に照射すると,電磁波は金属の内部まで進入し,自由電子はその電磁波の振動数で最も効率よく,揺れ動ごかされます。 この状況は,自由電子集団が(エネルギー無限大の)ポテンシャル壁に囲まれて,その中で振動していることと等しくなりますが,その振動状態が安定した定在波(疎密波)として存在できるためには,波長の整数倍がその振動範囲に等しくなければならないでしょう。 そのような集団のエネルギーは離散的な値をとることしかできず,集団はひと塊であたかも一つの粒子(準粒子)のように振る舞い,外界とエネルギーを交換します。このプラズマ周波数において観測される自由電子からなる準粒子をプラズモンといいます。 |