
| 10-2 交換子群と可解群 |  |
|
| f-denshi.com 更新日 23/05/21 間違い訂正 | ||
| [目次へ] | ||
| サイト検索 | ||
[1] ある群 G が与えられ,その正規部分群 H による剰余群 G/H を考えます。 一般に H が大きくなるほど G/H は小さな群となり,G/H が可換群となる可能性が高くなり(位数が2,3であれば,それは100%可換群群),この両者が密接に関係していると考えられます。その指針を与えてくれるのがここで述べる交換子群です。まず,その定義です。
|
交換子群 [定義] 群 G の部分群 H,K に対して, xyx-1y-1 : x∈H, y∈K ← [x,y] と書く と表せる元を交換子と呼ぶ。また,交換子から生成される(注意)群Gの部分集合は群をなし,交換子群と呼び,[H,K ]と書く。 [H,H ]≡D(H) と書く。 (注意:交換子全体の集合は群をなさない。あらゆる交換子の積から生じるすべての元を含めねばならない。) |
交換子は,x,y が可換のときは,[x,y]=xyx-1y-1=yxx-1y-1=e,
逆に,xyx-1y-1=e ならば,両辺に右から yx をかけて,xy=yx ,すなわち,
[x,y]=e ⇔ xy=yx
という関係が成り立っています。
交換子群は剰余群の可換性を評価するために利用されます。正規部分群Hの剰余類に,群の演算が,xH * yH = xyH と定義されており,かつ,xH と yH が可換,すなわち,xH * yH=yH * xH であれば,
xyH=yxH
と同じことですが,これに左からx-1y-1をかければ,
x-1y-1xyH=H
すなわち, x-1y-1xy∈H であること[#],x-1y-1xy が H からはみ出さないことが分かります。(元と逆元の表記を取り換えたものが上の囲みの定義)
特にG が可換群の場合,交換子群 [G,G ] は単位元のみからなる群 {e} であることはすぐにわかります。そして,剰余群 G/{e}=G も可換群です。
[2] 交換子群と正規部分群との関係を示す重要な定理を示します。
|
定理1 (1) [G,G ] はG の正規部分群である。 |
証明
(1) 任意の g∈G , xyx-1y-1∈[G,G ] に対して,
g(xyx-1y-1)g-1 = gxg-1gyg-1gx-1g-1gy-1g-1
=(gxg-1)(gyg-1)(gxg-1)-1(gyg-1)-1
と表せるので,g[G,G ]g-1 ⊂[G,G ]が示せます。これは[G,G ]が G の正規部分群であることの定義です[#]。
(2) 剰余類,x[G,G ],y[G,G ],x-1[G,G ],y-1[G,G ]∈G/[G,G ],とすれば [#],
x[G,G ]y[G,G ]x-1[G,G ]y-1[G,G ]=xyx-1y-1[G,G ]=[G,G ]≡E ←代表元を用いた剰余類の記号を使ってます[#]
ただし,Eはこの剰余群 G/[G,G]の単位元で[#],最後の=はxyx-1y-1∈[G,G ]だから[#]です。この式の右から(y[G,G ]x[G,G ])をかけると,
x[G,G ]y[G,G ]=y[G,G ]x[G,G ]
が示されます。
( G/[G,G] は,G においてすべての交換子を単位元とみなす関係を G に入れることで,これはすべての元を可換とみなす関係を導入することに等しく,その関係の入った同値類は可換となる,と考えることができる。)
(3) G/H,が可換群ならば,任意の xyx-1y-1について,
xyx-1y-1H = xH・yH・x-1H・y-1H
=(xH・x-1H)・(yH・y-1H)
=eH・eH
=H
これは,交換子 xyx-1y-1∈H を意味する。よって,この交換子から生成される交換子群[G,G]はHの部分群でなければならない。
(最後の(3)関係は交換子をそうなるように定義したので当たり前なんですが。)
[3] 以上の結果を正四面体群について確かめてみると,交代群A4 の交換子群は,
[A4 ,A4 ]={ e,hx,hy,hz }=H
であることは確かめられます[演習問題]。
H がA4 の正規部分群であることは本文中で示したとおりです[#]。そして, A4 /[A4 ,A4 ]= Z3 は可換群です。
[4] 対称群Snと交代群Anの交換子群は次のようになります。
|
定理2 (1) [Sn,Sn]=An [A2,A2]=e |
証明
(1)
n=2のときは,S2={e,(12)} は可換群で,[S2,S2]={e}=A2 であるから成り立つ。
n≧3のときは, x,y,x-1,y-1∈Sn として,交換子の置換の符号[#]について,
sgn xyx-1y-1 =sgn x sgn y sgn x-1sgn y-1 = +1
であるから,Snの交換子から生成される元の符号はすべて+1である。すなわち,
[Sn,Sn]⊂An
一方,An, n≧3 は長さ3の巡廻置換,(12k),k=3,・・・,n から生成される[#]が,
(12k)=(12)(1k)(12)-1(1k)-1 ←右辺はSnの元からなる交換子
と書くことができるので,
An⊂[Sn,Sn]
であることもわかる。したがって,[Sn,Sn]=An である。
(2)も(1)と同様なので省略。
(3)
n≦3のときは具体的に計算して確かめることができる。
n=4のときは,正規部分群Hの位数は4であるから,剰余群A4/Hの位数は,12/4=3である。ところが,位数3である群は可換群Z3に同型であるから,先程の定理1の(3)より,
[A4,A4]⊂H
である。 一方,Hの元について,
e =eee-1e-1
(12)(34)=(243)(142)(243)-1(142)-1 ⇔ hy=b1b3a1a3 =a4b2
(13)(24)=(243)(123)(243)-1(123)-1 ⇔ hx=b1b4a1a4 =a2b3
(14)(23)=(243)(134)(243)-1(134)-1 ⇔ hz=b1b2a1a2 =a3b4
と書くことができるので,H⊂[A4,A4]である。よって,H=[A4,A4]。
上式の3へ間違いを訂正しました。(23/05/21)
上の等式は,下表をよく見て確認してください。
x∈A4 の互換,巡回置換を用いた表示 e e a1 (234) b1 (243) hx (13)(24) a2 (143) b2 (134) hy (12)(34) a3 (124) b3 (142) hz (14)(23) a4 (132) b4 (123)
X・Y e hx hy hz a1 a2 a3 a4 b1 b2 b3 b4 e e hx hy hz a1 a2 a3 a4 b1 b2 b3 b4 hx hx e hz hy a4 a3 a2 a1 b2 b1 b4 b3 hy hy hz e hx a3 a4 a1 a2 b4 b3 b2 b1 hz hz hy hx e a2 a1 a4 a3 b3 b4 b1 b2 a1 a1 a2 a4 a3 b1 b4 b2 b3 e hz hy hx a2 a2 a1 a3 a4 b3 b2 b4 b1 hz e hx hy a3 a3 a4 a2 a1 b4 b1 b3 b2 hy hx e hz a4 a4 a3 a1 a2 b2 b3 b1 b4 hx hy hz e b1 b1 b4 b3 b2 e hx hz hy a1 a3 a4 a2 b2 b2 b3 b4 b1 hx e hy hz a4 a2 a1 a3 b3 b3 b2 b1 b4 hz hy e hx a2 a4 a3 a1 b4 b4 b1 b2 b3 hy hz hx e a3 a1 a2 a4
n≧5のとき,(1)の[Sn,Sn]=An と [An,An]⊂[Sn,Sn]から[An,An]⊂An は直ちにわかる。
一方,An, n≧3は長さ3の巡回置換,(12k),k=3,・・・,n から生成される[#]が,n≧5のときは,1,2,k のいずれとも異なる,2文字,i,jを用いて,
(12k)=(12i)(1kj)(12i)-1(1kj)-1
と表すことができる。これは,An ⊂[An,An]を意味する。先の結果と合わせて,An =[An,An]。 証明終
[5] 表記だけの問題ですが,A4/H=Z3を次のように書きます。
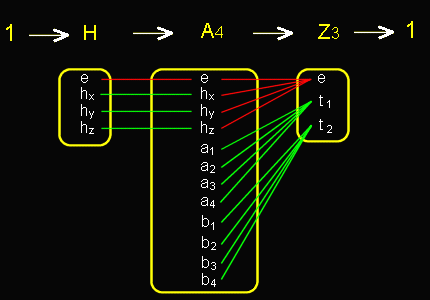
ここで,Z3のところは,A4/H と書いても構いません。
[1] 一般に,群 G について,その交換子群を考え,さらにその交換子群について,その交換子群を考えるということを繰り返し考えることができます。すなわち,
[G,G] ≡ D1(G)
[D1(G),D1(G)]≡ D2(G)
[D2(G),D2(G)]≡ D3(G)
・・・・・・・・・・・・・・・・・・・・・・・
このとき,次のような集合の包含関係,
G ⊇ D1(G) ⊇ D2(G) ⊇ D3(G) ⊇ ・・・・・
を交換子群列とよびます。そして,ある k から先について,
(1) Dk(G)=Dk+1(G)=・・・={e} ←可解群
(2) Dk(G)=Dk+1(G)=・・・≠{e}
の2とおりの場合が生じます。ここで,(1)となる場合,G を可解群といいます。
[2] 例えば,S4は,
D1(S4)=[S4,S4]=A4
D2(S4)= [A4,A4]=H
D3(S4)=[H,H]={e}
となるので可解群です。
S4交換子群列は,
S4 ⊃ A4 ⊃ H ⊃ { e } (攻めてる方向 ⇒ は大きい群から側から)
注意:H = Z2×Z2 は単純群ではないので,↑は組成列 [#] ではない。
この定義を用いると,1.の定理2から,
|
定理3 |
と述べることができます。これは,5次以上の一般代数方程式に解の公式が存在しないことを示すための重要な(補助)定理となっています。
[3] 交換子群を用いた定義のままでは,その意味を掴みにくいので,その同値な表現を与えることも無駄ではないでしょう。
| 定理4 群G が可解群であるための必要十分条件は,Gの部分群の列 G=G0 ⊃ G1 ⊃ G2 ⊃ ・・・ ( ⊃ Gm={e} ) ・・・・・・・・・ [*] において, (1) 各 Gkは Gk-1 の正規部分群である。 (2) 剰余群 Gk-1/Gk はすべて可換群である。 (k=1,2,・・・m) が成り立つことである。 |
これを可解群の定義とすることもできます。可解群は可換群を繰り返し拡大して得られる群です。
また,巡回群は可換群なので,(2)を巡回群としている教科書もあります。
[4] この2つの条件の他に,
(3) すべての Gk-1/Gk が{e}ではない単純群[#]である。
ことを満足するとき,部分群の列,
G=G0 ⊃ G1 ⊃ G2 ⊃ ・・・
を組成列と言います[#]。
対称群 Sn の組成列は,
S1 = e
S2 ⊃ A2=e
S3 ⊃ A3 ⊃ e
S4 ⊃ A4 ⊃ H ⊃ Z2 ⊃e
S5 ⊃ A5 ⊃ A5 ⊃ ・・・
[5] 組成列は,必ずしも有限で終わるものばかりとは限りません。例を挙げておくと,整数加群からつくられる部分加群の列,
Z ⊃ 2Z ⊃ 4Z ⊃ 8Z ⊃ ・・・・
は組成列です。剰余群は,nZ/2nZ=Z2 (可換群)。
定理4の略証
可解群ならば,交換子群列が(1),(2)を満たしていることは明らか。逆に[*]が (1),(2) を満たしているならば,定理1の(3) [#] より,
G0/G1が可換群 ⇒ D1(G0)=[G0,G0]⊂G1
G1/G2が可換群 ⇒ D2(G0)=[D1(G0),D1(G0)]⊂[G1,G1]⊂G2
:
Gm-1/Gmが可換群 ⇒ Dm(G0)⊂ ・・・ ⊂ ・・・ ⊂Gm ={e}
が成り立つ。すなわち,これはGが可解群であること,Dm(G)={e}を示している。
[6] 他に重要な定理として,以下のものがあります。
| 定理 (1) 群 G が可解群 ⇒ そのすべての部分群 Sも可解群である。 (2) 群 G が可解群 ⇒ そのすべての剰余群 G/S も可解群である。 (3) 群 G の正規部分群 H とその剰余群 G/H がともに可解群 ⇒ G は可解群である。 (4) 巡回群,および,巡回群の直積 [#] は可解群である。 |
証明略
| 定理 群 G の位数|G|が奇数ならば,G は可解群である。 |
証明略
|
Burnsideの定理 位数がpmqn の群は可解群である。 |
証明略
ここでは,[G,G]タイプの交換子群について述べましたが,[G,H]タイプについては,Appendix5 冪零群にまとめています,
|
定理 位数がpr の群はべき零群である。 |
証明略