| 11 一般固有空間 | ||
| f-denshi.com [目次] 最終更新日: 16/12/07 | ||
| サイト検索 | ||
ここでは正規行列に限らず,一般的な正方行列について考えます。4において,固有多項式が重根をもつ場合も含めて,ベクトル空間V上の線形演算子Tが対角化可能である必要十分条件が,「V がTの各固有空間によって直和分解されていること」を示しましたが,ここでは,どのようなTであっても,一般固有空間によって直和分解される(一般固有値問題)ことを説明します。また,具体的な直和分解の方法としてジョルダンの標準形を紹介します。
[1] 固有多項式が重根をもつ場合の固有空間について考察しましょう。線形写像 f : V→V の表現行列をT (n 次正方行列 )とします。また,この固有多項式を,
| ΦT(λ)=(λ−λ1)d1(λ−λ2)d2・・・(λ−λm)dm : n = d1+d2+・・・+dm |
とします。つまり,固有値は,λ1,λ2,・・・,λm で各固有値の重複度は, d1,d2,・・・,dm (>0)とします。ここでの最初の目的は,
| 定理1 重複した固有値をもつ線形演算子Tは適当な正則行列Pによって, のように変換可能である。ただし,線形演算子(正方行列)Tk,( k=1,2,・・・,m ) の次元と固有多項式はそれぞれ, (1) dimTk = dk (2) ΦTk(λ) = (λ−λk)dk を満たしている。 |
||||||||||||||||
ということを示すことです。言い換えると,Tを基底変換によって適当にブロック化してやると,固有値ごとの部分ベクトル空間に分類することができ,その部分ベクトル空間の次元は対応する固有値の重複度に等しいということです。
[2] 証明はまず,一般固有空間と呼ばれるV の部分集合の定義から始めましょう。固有値λkに対応する固有方程式[#]を,
(λkE−T)x = 0, ・・・・・・・・・・・・・・ [*] (E:単位行列)
と書けば,固有空間 E(λk) [#] は,連立1次同次方程式の解空間 [#] とみることもできました。すなわち,
E(λk)=Ker(λkE−T) ≡{ x |(λkE−T)x = 0 }
となります。 (符号を逆にして,{ x |(T−λkE)x = 0 }としてもよい。)
[3] ところで,一般に線形写像 g : V → V の表現行列[#]をG とすれば,
0 ⊆ Ker G ⊆ Ker GG ⊆ ・・・⊆ Ker Gk ⊆ ・・・ ( Ker GG ⇔ Ker gOg など )
のような ”V の部分空間の包含関係の列” が存在します。この様子は下の図のように示すことができます。
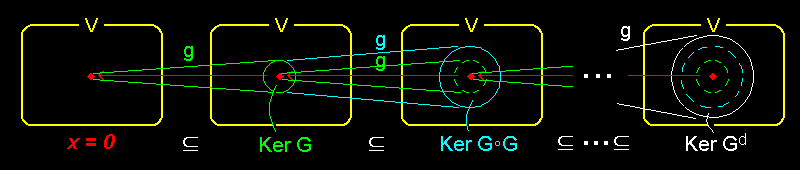
もちろん,この・・・ の右の先にある集合がV を超えて大きくなることはありません。なおかつ,上の各包含関係において等号が成り立たないときは少なくとも右に置かれている部分空間の次元が左のものより1以上大きくなるので,いつかは,
あるd が存在して, Ker Gd-1 ⊂ Ker Gd = Ker Gd+1 = Ker Gd+2 = ・・・ ⊆V
とこの系列におけるV の最大の部分集合(部分ベクトル空間) Ker Gd に到達し,それ以上はk を大きくしても集合Ker Gkは変化しなくなります。
⇒ きちんとした証明→ [a1]
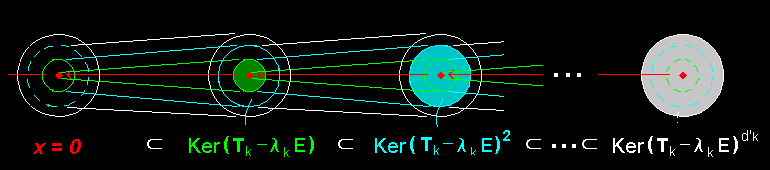
ここで,G として,先の (λkE−T) を当てはめれば,
| 0 ⊂ Ker(λkE−T)⊂ Ker(λkE−T)2 ⊂・・・⊂ Ker(λkE−T)d ⊂ V ・・・・ [**] |
の包含関係の列が存在することがわかります。
[3] 以上の前置きの下で,線形写像 f :V → V ( f の表現行列をTとする )の固有値多項式が,
Φf(λ)≡ΦT(λ)=(λ−λ1)d1(λ−λ2)d2・・・(λ−λm)dm : n = d1+d2+・・・+dm
であるとき,” λkに関する一般固有空間:E ~(λk) ” (k=1,2,・・・,m) と呼ばれるV の部分集合を次のように定義します。
| 一般固有空間(または広義固有空間): E ~(λk) ≡{x ∈V|ある自然数 d'k が存在して,(λkE−T)d'k x = 0 } また,一般固有空間に属するベクトルx を一般固有ベクトルといいます。 |
つまり,一般固有空間とは[2]で述べた系列の行き着くところの最大部分集合のことであり,[**]において,d をd'k と書き換えたものが上の定義です。
[4] このとき,次の関係が成り立ってます。
(0) x ∈E ~(λk) であるならば,Tx ∈E ~(λk) である。
この性質を,「 E ~(λk)はTの不変部分空間,または, T-不変 である。」( または,f -不変 ) と言います。
証明
x ∈E ~(λk),つまり,(λkE−T)d'k x = 0 であるとき,TはEともTとも可換であるから,次のような計算,
(λkE−T)d'k ( Tx ) = T((λkE−T)d'k x )= T0 = 0
ができます。これは,Tx ∈ E ~(λk) であることを示しています。
[5] さらに次の定理が成り立ちます。(ここまで(λkE−Tk) で考えてきたが,符号を逆にした(Tk−λkE)をこれ以後考える。 )
定理2
(1) 線形写像 f (演算子T:V →V ) の E ~(λk)への制限を h とすると,それに対応する行列 (Tk−λkE) はベキ零行列である。
(ここで,E は,Tk と同じ次数 の単位行列である。)
(すなわち,V は一般固有空間の直和で表すことができる。
(2) V =E ~(λ1) E ~(λ2) ・・・ E ~(λm) [直和分解]
(3) dimE ~(λk)= dk
ここで,ベキ零行列についてはAppendix3[#] を見てください。
まず,(1)は,[**]の言い換えに過ぎないので問題ないでしょう。写像h はf の定義域を,E ~(λk) ,すなわち,Ker(λkE−T)d'k に制限した写像なので,すべての元は少なくとも d'k 回のh の作用(=(λkE−Tk)d'k )で必ず0 に移ります。なお,(λkE−Tk) のままでもよいのですが,慣習にしたがい,下に示すように符号を逆にして(Tk−λkE)で考えることにします。 )
[7] (2)の証明には予備知識が入ります。
まず,固有多項式:
| ΦT(λ)=(λ−λ1)d1(λ−λ2)d2・・・(λ−λm)dm : n = d1+d2+・・・+dm |
最小多項式 [#]:
φ(λ)=(λ−λ1)d'1(λ−λ2)d'2・・・(λ−λm)d'm
φ(T)=(T−λ1E)d'1(T−λ2E)d'2・・・(T−λmE)d'm
=0
ただし, 1≦d'k≦dk , (k=1,2,・・・,m) とします。
さらに,最小多項式のk番目の因子を除した多項式,
|
を定義します(k=1,2,・・・,m)。すると,各φk(λ)は互いに素な多項式となっていることに注意してください。(すべてのφk(λ)を割る最大公約式は1である。)
[8] ここで,多項式に関するユークリッドの互除法に関わる定理を証明なしで示しておくと,
定理 多項式,
φ1(t),φ2(t),・・・,φm(t)が互いに素であれば,適当な q1(t),q2(t),・・・,qm(t) が存在して,
q1(t)φ1(t)+q2(t)φ2(t)+・・・+qm(t)φm(t) = 1とすることができる。(証明略)
そこで,この定理を互いに素なm個のφk(λ)に適用すると,
q1(λ)φ1(λ)+q2(λ)φ2(λ)+・・・+qm(λ)φm(λ) = 1 ・・・・ (8)
ですが,ここで,λ→T,1→E とすれば,恒等式,
q1(T)φ1(T)+q2(T)φ2(T)+・・・+qm(T)φm(T) = E
も成り立ちます。
ここで,
Qk=Qk(T)≡qk(T)φk(T)
とおけば,先の恒等式は,
Q1+Q2+・・・+Qm=E ・・・・・・(10)
と書けます。一方,QjQk=qj(T)qk(T)φj(T)φk(T) については,j≠k ならば,φj(T)φk(T) の部分はかならずφ(T)を因子に持つ(つまり,QjQkがφ(T)=0を因子にもつ)ことから,
QjQk=0
であることが分かります。
[9] 次に,このQkによるV の像をVkと書くことにします。すなわち,
Vk={Qkx|x∈V} ・・・・・・(11)
すると,任意のx∈V に対して,(10)を用いて,
x =Ex=(Q1+Q2+・・・+Qm)x
=Q1x+Q2x+・・・+Qmx
と表されます。すなわち,V の任意の元は,V1,V2,・・・,Vmの元の和で表すことができます。
このままでもいいのですが,xk≡Qkx と記号を導入すれば,V の任意の元x は,
x =x1+x2+・・・+xm xk∈Vk
と書くことができるということもできます。その一意性については,QjQk=0 を用いて証明することができます(演習問題)。
ここまでをまとめておくと,(11)に定義されたVkを用いることで,
V はV1,V2,・・・,Vm の直和に分解される。
[10] そして,このVkがE ~(λk)に等しいことが以下のように証明できます。
Vk⊂E ~(λk) の証明
Vkの任意の元xkについて,
xk=Qkx =qk(T)φk(T)x
の左から(Tk−λkE)d'k をかけると,
(Tk−λkE)d'k xk=(Tk−λkE)d'k qk(T)φk(T)x
= qk(T){(Tk−λkE)d'k φk(T)}x
= qk(T)φ(T)x ← (7)を見よ。
=0 ∵ φ(T)=0 なので,
すなわち,xk∈ E ~(λk) である。
[11] 次に上の逆を示します。
E ~(λk)⊂Vk の証明
E ~(λk)の任意の元xkについて,
(Tk−λkE)d'k xk=0
であるとすると,適当な x∈V を用いて,
xk=qk(T)φk(T)x
=Qkx ( ∈Vk )
と表される。
なぜならば,qk(λ)φk(λ)と(λ−λk)d'k は互いに素であるから ⇒[h5],適当な多項式 r(λ),s(λ) が存在して,
r(λ)(λ−λk)d'k +s(λ)qk(λ)φk(λ)=1
とできる。λ→T,1→E とすれば,
r(T)(T−λkE)d'k +s(T)qk(T)φk(T)=E
上式に右からxk をかけて,第1項が(T−λkE)d'k xk=0 となることに注意すれば,
qk(T)φk(T)s(T)xk=xk ⇔ Qks(T)xk=xk
ここで,s(T)xkはV の元であることには違いないので,結局,この式は,「xk=Qkx ただし,x∈V 」 を意味する。
すなわち,xk∈Vkである。
以上から,Vk=E ~(λk),すなわち,ベクトル空間V は一般固有空間によって直和分解されることが証明されました。
しかし,この辺は抽象的で分かりにくいので,具体的に問題を解いてみる方が良いでしょう ⇒ 例題1[#]
[12]
定理2の(3)の証明
正方行列Tの最小多項式とは,Tの零化多項式の中で次数が最小で,最高次数の係数が1であるものをいいます (3-2ページ)[#]。したがって,最小多項式とはすべての零化多項式を整除する多項式ということもできます。
そこで,d'k次ベキ零行列,Tk−λkE の固有方程式Φ(Tk−λkE)(μ) はμd'k である[Appendix3]ということから,
μd'k = Φ(Tk−λkE)(μ)=|μE−(Tk−λkE)|=|(μ+λk)E−Tk|
と変形し,ここで,μ+λk=t と変数を置き換えれば,この式の両端は,
(t−λk)d'k =|tE−Tk|
と書けます。この式は,Tk の固有多項式が,ΦTk(t)=(t−λk)d'kであることを示しています。したがって,
dimE ~(λk) = d'k = dimTk (=dk)
(一部省略)
[a1] の証明
d'≧d のときの部分空間: Ker (λkE−T)d' はすべてKer (λkE−T)d に等しいことの証明
⇔ Ker (λkE−T)d=Ker (λkE−T)d+1 ⇒ Ker (λkE−T)d+2=Ker (λkE−T)d+1 であることを示せばよい。
[証明 ]
x ∈Ker (λkE−T)d+2
⇒ 0 =(λkE−T)d+2x =(λkE−T)d+1{(λkE−T)x }
⇒ {(λkE−T)x }∈Ker (λkE−T)d+1=Ker (λkE−T)d
⇒ 0 =(λkE−T)d{(λkE−T)x }
=(λkE−T)d+1x
⇒ 最後の行は, x ∈Ker (λkE−T)d+1 を意味する。
すなわち,Ker (λkE−T)d+2 ⊆ Ker (λkE−T)d+1 であることを示しているが,一般に,Ker Gd+1 ⊆ Ker Gd+2なので,
Ker (λkE−T)d+2 = Ker (λkE−T)d+1
と等号が成立する。
[h5] の証明
q1(λ)φ1(λ)+q2(λ)φ2(λ)+・・・+qm(λ)φm(λ) = 1 ・・・・ (8)
の第k項 qk(λ)φk(λ)に着目すると,もし,これが(λ−λk)と共通因子をもつならば,他のj 項 (j≠k)は(λ−λk)と共通因子をもつので,左辺全体が(λ−λk)で整除可能であることになる。ところが,(8)の右辺=1は(λ−λk)で整除不可能であるからこれは矛盾である。したがって,qk(λ)φk(λ)と(λ−λk)とは互いに素である。
[12] 正方行列Tを相似変換によって一般固有空間E~(λk)の直和で表すとき,特に各ブロックをdk個の1次独立なベクトル,(Tk−λkE)dk-1tk ,・・・,(Tk−λkE)tk,tkを用いて変換した表現行列をジョルダンの標準形といいます。
具体的には,一般固有空間は下記のジョルダン細胞となり,Tはこのジョルダン細胞の直和となります。
Jk≡
λk 1 O : ・・ O λk 1 λk
J1 O
J2 O :
Jm Jk: ジョルダン細胞 ジョルダンの標準形
Jkは正方行列の次数によって,
| 1次:λk,2次:Jk≡ |
|
,3次: |
|
,4次: |
|
,n次:J(λ,n) |
などである。ジョルダン細胞の特徴は,
|
|||||||||||||||||||
対角化とは,ジョルダン標準形において,すべての dimJk=1 という特別な場合であることがわかります。
このような変形が可能なこと(及び,そのときの条件)の証明は,PDF を見てください。
[13]途中で,次の命題を用いてますが,ベキ零行列を参考にせよ⇒[#]
| 命題 次の0 でない,dk個のベクトルは互いに1次独立である。 (Tk−λkE)dk-1t k , ・・・ , (Tk−λkE)t k,t k |
とにかく,ジョルダンの標準形への変換は具体的な計算を行ってみるのが理解の早道です。
具体例を示しますが,そのあとで適当な演習書の問題をぜひ自力で解いてください。線形代数の知識をフル活用しますのでたいへんよい復習にもなります。
3次元ベクトル空間V からV への線形演算子T をジョルダン標準形へ導け。
T =
-3 4 -3 -1 1 -1 0 0 -1 , T: V →V
固有多項式: ΦT(λ)=|λE−T|=(λ+1)3 ,
固有値: λ=-1
固有値λ=-1に対して,(T−λE)は,
| T+E= |
|
,(T+E)2 = |
|
,(T+E)3=O |
よって,最小多項式は3次で,φ(λ)=(λ+1)3 ← ジョルダン細胞の最大次数=3 とわかる。
したがって,答えは,
J(-1,3)=
-1 1 0 0 -1 1 0 0 -1
であることはこの時点で判明するのですが,ここでは一般固有値問題の解き方の勉強ということで,正攻法で解くことにします。次にすべきことは固有空間を求めることです。
| (T+E)x = |
|
= |
|
,ただし, | x= |
|
を解いて, x3=0, x1=2x2 が得られるので,λ=−1に対する固有空間は,
E(-1)=u1=x2
2 1 0 =x2t1 x2∈R ← Tu1=−u1 ,Tt1=−t1
↑ ジョルダン細胞の個数=1 とわかる。
以上のように固有ベクトルは1つしかないことを確認。次の一般固有空間を考える。
(T+E)2x =
2x3 x3 0 =
0 0 0
これより,x3=0 が得られるので,上式を満たす一般固有空間(下図V2)は,
E~(-1) ⊃ x1
1 0 0 +x2
0 1 0 ≡u2, x2,x1∈R ⇔ (T+E)2u2=0
| そこで,u2 と1次独立である t3≡ |
|
を一つ定めて, |
(T+E)t3 =
-3 -1 0 ≡t2 ⇔ Tt3=−t3+t2
(T+E)2t3=(T+E)t2 =
2 1 0 =t1 ⇔ Tt2=−t2+t1
を定義する。ここで,(T+E)3=Oに 注意すれば,
0 =(T+E)3t3=(T+E)2t2=(T+E)t1 ⇔ Tt1=−t1
であることも確かめられる。また,1次独立なt1,t2,t3 [#]は,E~(-1) を張る基底であると同時にVも張ります。
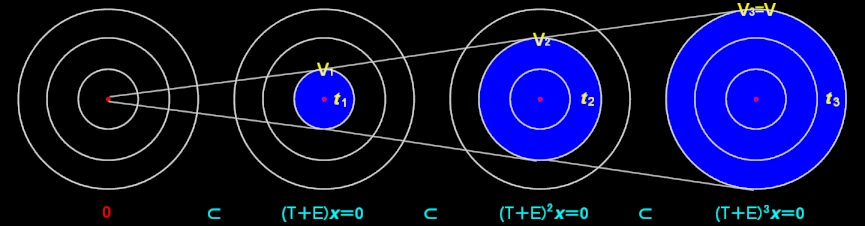
この様子は上図のように図示できる。 ただし,Vk={x|(T+E)kx=0}とする。
そして,t1,t2,t3 をこの順に並べて作った正則行列,
P=
2 -3 0 1 -1 0 0 0 1 ,P-1=
-1 3 0 -1 2 0 0 0 1
を用いて基底変換すれば,
P-1TP =
-1 1 0 0 -1 1 0 0 -1
とジョルダンの標準形になる。
3次元ベクトル空間V からV への線形演算子T をジョルダン標準形へ導く。
T =
0 2 1 -4 6 2 4 -4 0 , T: V →V
固有方程式: ΦT(λ)=(λ−2)3 , 固有値:λ=2
最小多項式: φ(λ)=(λ−2)2 ← ジョルダン細胞の最大次数=2
固有値λ=2に対して
T−2E =
-2 2 1 -4 4 2 4 -4 -2 , (T−2E)2 =
0 0 0 0 0 0 0 0 0
固有空間は,
(T−2E)x =
-2x1+2x2+x3 -4x1+4x2+2x3 4x1−4x2−2x3 =
0 0 0 ← (E−2T)x = 0 と同じ
を解いて,-2x1+2x2+x3 =0 が得られるので,λ=2に対する固有空間は,
E(2)=u1=x1
1 0 2 +x2
0 1 -2 , x1,x2∈R ⇔ Tu1=2u1
↑ ジョルダン細胞の個数=2
| そこで,t2≡ |
|
とすると,これは E(2)を法として1次独立であるから, |
(T−2E)t2 =
2 -4 4 ≡t1 ≠0 ⇔ Tt2=2t2+t1
が得られ,また,
0 = (T−2E)2t2 =(T−2E)t1 ⇔ Tt1=2t1
であることもわかる。とすれば, E~(2) を張る基底を定めることができる。
そして,E(2)の基底ベクトルの中のどちらか,たとえば,
t3=
1 0 2
をt3 とすれば,t1,t2,t3 をこの順に並べて作った行列,
P=
2 1 1 -4 0 0 4 0 2 ,および,P-1=
1 8
0 -2 0 8 -8 -4 0 4 4
を用いると,
P-1TP =
2 1 0 0 2 0 0 0 2
|
もちろん,固有ベクトルとして,
を選んでt1,t2,t3’をこの順に並べて作った行列,
を用いても,
と同じ結果を得ます。 OK |
もし,基底の並びをt3’,t1,t2 として,
P=
0 -2 1 1 -4 0 -2 4 0
を定めると,ジョルダン標準形は,
P-1TP =
2 0 0 0 2 1 0 0 2
となり,1次のジョルダンブロックが左下にきます。
3次元ベクトル空間V からV への線形演算子T をジョルダン標準形へ導く。
T =
3 -3 -2 0 2 0 1 -2 0 , T: V →V
固有方程式: ΦT(λ)=(λ−1)(λ−2)2 , 固有値:λ=1,2
最小多項式: φ(λ)=(λ−1)(λ−2)2
固有値λ=1に対して
T−1E =
2 -3 -2 0 1 0 1 -2 -1
固有空間は,
(T−E)x =
2x1−3x2−2x3 x2 x1−2x2−x3 =
0 0 0 ← (E−T)x = 0 と同じ
を解いて, x2=0, x1−x3=0 が得られるので,λ=1に対する固有空間は,
E(1)=u1=x3
1 0 1 x3∈R
となる。 また,1次元では一般固有空間と固有空間に等しい。
| ここで,固有ベクトル t3≡ |
|
と定義すれば, Tt 3= 1t3 が成り立つ。 |
固有値λ=2に対して
T−2E =
1 -3 -2 0 0 0 1 -2 -2 , (T−2E)2 =
-1 1 2 0 0 0 -1 -1 2
固有空間は,
(T−2E)x =
x1−3x2−2x3 0 x1−2x2−2x3 =
0 0 0
を解いて, x2=0, x1−2x3=0 が得られるので,λ=2に対する固有空間は,
E(2)=u2=x3
2 0 1 x3∈R
となる。これは1次元のため,先のE(1)の固有ベクトルと合わせて3次元空間V を張ることはできない。
そこで,λ=2に対応する一般固有空間E~(2)を考えるが,E~(2)が2次元であることに注意して,
(T−2E)2x =
-x1+x2+2x3 0 -x1+x2+2x3 =
0 0 0
これより,-x1+x2+2x3=0 が得られるので,λ=2に対する一般固有空間は,
E~(2)=x2
1 1 0 +x3
2 0 1 , x2,x3∈R ⇔ (T−2E)2t2=0
| したがって,t2≡ |
|
とすると,これは E(2)を法として1次独立であるから, |
(T−2E)t2 =
-2 0 -1 ≡t1 (∈E(2), ≠0) ⇔ Tt2=2t2+t1
とすれば,t2とともに E~(2) を張ることのできる基底ベクトルt1 (≠0,∈E(2)))を定めることができる。また,t1 は
(T−2E)t1 =(T−2E)2t2 =0 ⇔ Tt1=2t1 (=−u2()
という関係にある。
そして,t1,t2,t3 を並べて作った行列,
P=
-2 1 1 0 1 0 -1 0 1 ,および,P-1=
-1 1 1 0 1 0 -1 1 2
を用いると,
P-1TP =
2 1 0 0 2 0 0 0 1
となる。
もし,途中で,t2の代わりに
| t2’≡ |
|
は E(2)を法として1次独立でないから不適当である。 |
| しかし,t2+t2’= |
|
=t2”とすると, |
| (T−2E)t2”= |
|
≡t1” |
を計算して,t1”,t2”,t3 を並べた変換行列,
| P= |
|
,および,P-1= |
|
を用いれば,
| P-1TP = |
|
とやはり,ジョルダン標準形が導かれます。
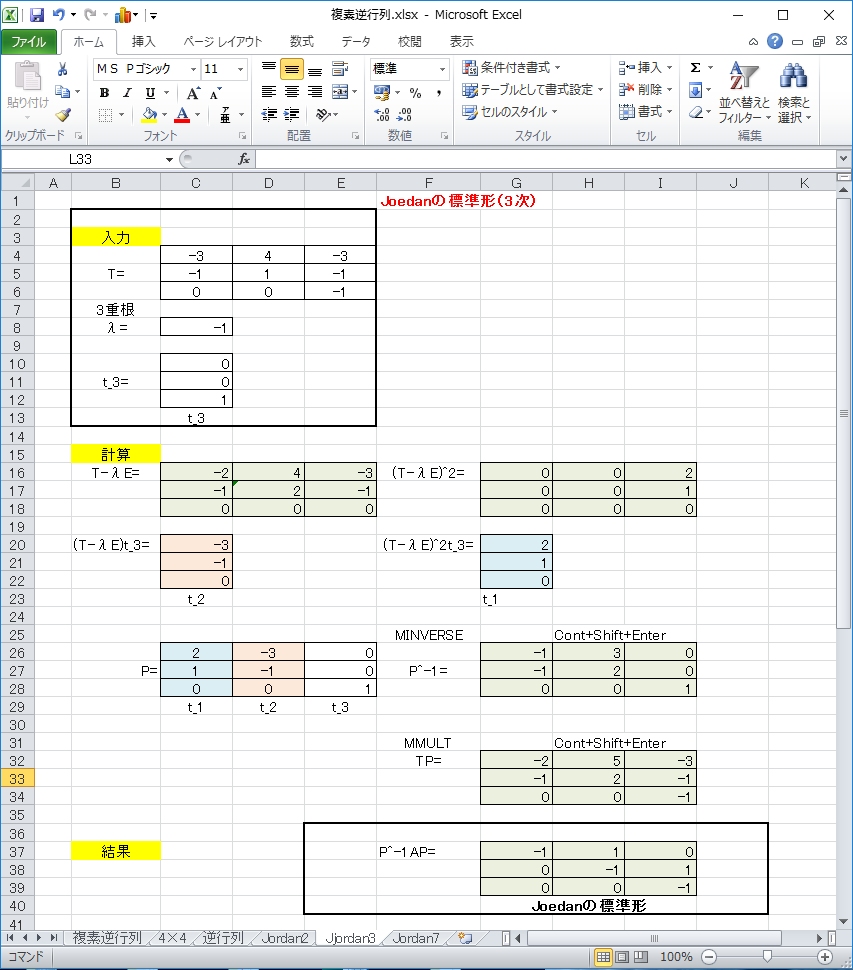
例題1の解法=1 excel で計算するフロー