 |
t115 理想フェルミ気体 |
| f-denshi.com 更新日: 21/12/12 |
| サイト検索 |
| 目次へ |
1.フェルミ統計の基本事項
理想フェルミ気体はフェルミ統計に従う理想気体のことで,金属の自由電子モデルなどを記述するために用いられます。フェルミ統計
[#] について復習しておくと,
一般的なグランドカノニカルアンサンブルにおいて,μ, T が定められたときの大配関数は,
| Ξ (μ, T)= |
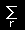 |
exp |
 |
Nrμ−Er |
 |
(2.159) |
|
| kT |
で与えられます。ここでr はすべての微視的状態にわたって和をとります。これは1種類の粒子からなる系がフェルミ統計に従う場合は次のようにも書くことができます。
ΞF=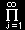 Ξjf フェルミ粒子の大分配関数 (2.160)
Ξjf フェルミ粒子の大分配関数 (2.160)
ただし, j はエネルギー固有状態に対して付けられた番号で,
Ξjf = 1+ exp [ - (εj −μ)/kT]
= 1+ξ exp (-εj/kT) (2.161)
( μ = kT log ξ )
エネルギーがεj にある粒子数の期待値 (=フェルミ分布関数) は,
| fF(εj) = <nj>f = |
1 |
|
|
| exp {(εj−μ)/kT}+1 |
| = |
|
1 |
(2.162) |
|
| ξ-1exp {εj/kT}+1 |
さらに,エネルギー準位εj の縮退がΔj であるときは,
| fF(εj) = <nj>f = |
Δj |
|
|
| exp {(εj−μ)/kT}+1 |
| = |
|
Δj |
(2.163) |
|
| ξ-1exp {εj/kT}+1 |
と書き換えなければなりません。すると,系の全粒子数,エネルギーは,
| N = |
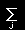 |
<nj >f = |
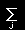 |
Δj |
(2.164) |
|
| ξ-1exp {εj/kT}+1 |
| E = |
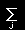 |
<εj >f = |
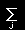 |
εjΔj |
(2.165) |
|
| ξ-1exp {εj/kT}+1 |
で与えられます。また,グランドポテンシャル,状態方程式は,
| J = −kT |
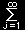 |
Δj log { 1+ξexp (-εj/kT) } |
|
|
| PV |
= |
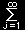 |
Δj log { 1+ξexp (-εj/kT) } (2.167) |
|
| kT |
となります。
2.フェルミ-ディラック積分表示
1.で示した式を積分表示とするために,エネルギーの連続関数としての状態密度を
D(ε),電子スピンなどの内部自由度を g (=2 スピン考慮するとき) として,和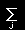 を積分に置き換えると,
を積分に置き換えると,
| N = |
 |
gD(ε) |
dε
(2.168) |
|
| ξ-1exp {ε/kT}+1 |
| E = |
 |
gεD(ε) |
dε (2.169) |
|
| ξ-1exp {ε/kT}+1 |
| J = −kT |
 |
gD(ε)log { 1+ξexp (-ε/kT) }dε |
|
|
| P = |
kT |
= |
 |
gD(ε) log { 1+ξexp (-ε/kT) }dε |
|
| V |
となります。
そして,具体的な D(ε) として,3 次元自由粒子に対する1粒子状態密度 [#],
を適用した系をフェルミ理想気体と呼びます。
フェルミ理想気体の性質はこれらの積分を実行し,必要となる熱力学関数に変換していけばよいことになります。
粒子数
粒子数については,(2.173) 式において,ε/kT = x,dε = kTdx と変数変換を行えば,
| N = |
2gV |
 |
2πmkT |
 |
3/2 |
|
 |
|
|
 |
x |
|
dx (2.177) |
|
|
|
|
|
|
 |
π |
|
h2 |
|
ξ-1ex+1 |
と書くことができます。残念ながら古典理想気体の場合 [#] とは違い,この定積分は数値計算によってしか解くことができません。そこで,次式で定義されるフェルミ-ディラック積分と呼ばれる関数で表すことにします。
フェルミ-ディラック積分
| f(n,ξ)= |
1 |
 |
xn-1 |
dx |
|
|
| Γ(n) |
ξ-1ex+1 |
|
今ここで,必要な値は,n=3/2 のときで,それは,
| f(3/2,ξ)= |
2 |
|
 |
|
|
 |
x |
|
dx (2.179) |
|
|
|
|
 |
π |
|
ξ-1ex+1 |
さらに,熱 ド・ブロイ波長
|
|
|
| λ(T) = h/ |
 |
2πmkT |
|
を用いれば,(2.177) 式は,
| N = |
gV |
|
f(3/2,ξ) [粒子数] |
|
| λ(T)3 |
| ρ= |
N |
|
= |
g |
|
f(3/2,ξ) [粒子数密度] ・・・ [*] (2.180) |
|
|
| V |
λ(T)3 |
|
と表されます。
- 内部エネルギー -
内部エネルギーについても同様な計算を進めると,
| E =2πgV |
 |
2m |
 |
3/2 |
|
 |
|
|
|
 |
ε |
ε |
|
dε |
|
|
|
| h2 |
|
ξ-1exp {ε/kT}+1 |
| = |
3 |
kTgV |
4 |
 |
2πmkT |
 |
3/2 |
|
 |
x3/2 |
dx |
|
|
|
|
|
| 2 |
|
|
|
| 3 |
 |
π |
|
h2 |
|
ξ-1ex+1 |
| = |
3kTgV |
f(5/2,ξ) (=(3/2)PV ) (2.181) |
|
| 2λ(T)3 |
ここで,フェルミ-ディラック積分 (n = 5/2),
| f (5/2, ξ ) = |
4 |
|
 |
x3/2 |
dx (2.182) |
|
|
|
|
|
| 3 |
 |
π |
|
ξ-1ex+1 |
を途中で用いました。さらに,(2.180) 式を用いて N, T の関数で表せば,
| E= |
3 |
NkT |
f (5/2, ξ ) |
[任意温度] (2.183) |
|
|
| 2 |
f (3/2, ξ ) |
- 定積比熱 -
内部エネルギーがわかれば,定積比熱は定義に従ってすぐに計算できます。その準備のために,(2.180) の右側 ( ) の式をρ = 一定(体積,粒子数とも一定) の条件下で微分すると,
| 0 = − |
3g |
|
dλ(T) |
|
f(3/2,ξ)+ |
|
g |
|
f(3/2,ξ) |
|
∂ξ |
|
|
|
|
|
| λ(T)4 |
dT |
λ(T)3 |
∂ξ |
∂T |
さらに
| dλ(T) |
= − |
λ(T) |
および,公式 |
d f (n, ξ ) |
= |
f (n−1, ξ ) |
|
|
|
|
| dT |
2T |
∂ξ |
ξ |
を用いれば, (Appendix A.3.2 参照)
 |
∂ξ |
 |
ρ=一定 |
= − |
3ξ |
|
f (3/2, ξ ) |
[絶対活動度の温度変化] (2.186) |
|
|
|
| ∂T |
2T |
f (1/2, ξ ) |
この関係式を用いて定積比熱は,
| Cv= |
 |
∂E |
 |
ρ=一定 |
|
|
| ∂T |
| = |
 |
∂ |
|
 |
3 |
NkT |
f (5/2, ξ) |
  |
ρ |
|
|
|
| ∂T |
2 |
f (3/2, ξ ) |
| = |
|
3 |
Nk |
f (5/2, ξ) |
+ |
|
3 |
NkT |
 |
∂ |
 |
f (5/2, ξ) |
 |
|
・ |
∂ξ |
|
|
|
|
|
|
|
| 2 |
f (3/2, ξ) |
2 |
∂ξ |
f (3/2, ξ) |
∂T |
| = |
|
3 |
Nk |
f (5/2,ξ) |
|
|
|
| 2 |
f (3/2,ξ) |
| + |
Nk |
3T |
 |
f (3/2,ξ)/ξ)f (3/2,ξ)−f (5/2,ξ)f (1/2,ξ) |
 |
 |
- |
3ξ |
|
f (3/2,ξ) |
 |
|
|
|
|
| 2 |
f (3/2,ξ)2・ξ |
2T |
f (1/2,ξ) |
いくつかの項は相殺されて,
| Cv= |
Nk |
 |
15 f (5/2, ξ) |
− |
9 f (3/2, ξ) |
 |
[任意温度] (2.188) |
|
|
| 4 f (3/2, ξ) |
4 f (1/2, ξ) |
となります。
- 圧力,状態方程式,グランドポテンシャル -
次に圧力ですが,(2.176) より,
| P=2πgkT |
 |
2m |
 |
3/2 |
|
 |
|
|
|
|
 |
ε |
log { 1+ξexp (-ε/kT) } dε |
|
|
|
| h2 |
|
まず,部分積分すると,
| P=[ 0 の項]−2πgkT |
 |
2m |
 |
3/2 |
|
 |
2 |
ε3/2 |
ξexp (-ε/kT) |
・ |
-1 |
dε |
|
|
|
|
|
| h2 |
|
3 |
1+ξexp (-ε/kT) |
kT |
| = |
4πgkT |
 |
2m |
 |
3/2 |
|
 |
|
|
|
 |
ε |
ε |
|
・ |
1 |
dε |
|
|
|
|
|
| 3 |
h2 |
|
ξ-1exp (-ε/kT)+1 |
kT |
ここで,変数変換 ε=kT x を行うと,
| = |
4gkT |
 |
2πmkT |
 |
3/2 |
|
 |
x3/2 |
|
dε |
|
|
|
|
|
|
|
| 3 |
 |
π |
|
h2 |
|
ξ-1ex+1 |
さらに,フェルミ-ディラック積分 (n = 5/2) とλ(T) を用いれば,
| P = |
|
gkT |
f (5/2,ξ ) |
|
[任意温度] (2.192) |
|
| λ(T)3 |
と書くことが可能です。さらに,(2.180) を用いて粒子数 N で表すと,
| PV = |
|
NkT |
f (5/2,ξ ) |
|
 |
= |
2 |
E=−J |
 |
[任意温度] |
|
|
| f (3/2,ξ ) |
3 |
と状態方程式を書き下ろすことができます。
- ヘルムホルツ自由エネルギー,エントロピー -
(2.180) とμ= kT log ξ ,G=Nμ を用いて,F = G−PV = Nμ− PV を計算すれば,
| F =NkT |
 |
logξ− |
f (5/2,ξ ) |
|
 |
|
|
| f (3/2,ξ ) |
また,このF と先程求めたE,(2.183) 式から,エントロピーは,
| S = |
E−F |
=Nk |
 |
f (5/2,ξ ) |
−logξ |
 |
・・・ (2.195) |
|
|
| T |
f (3/2,ξ ) |
と表すことができます。
3. 絶対零度の理想フェルミ気体
次に極端な温度として絶対零度におけるフェルミ分布関数の近似形を考えてみましょう。
まず,T → 0 とすると,フェルミ分布関数はステップ関数となります。
| fF(ε) = |
1 |
= |
 |
1 ε≦μ(=εF) のとき |
|
|
|
| exp ((ε−μ)/kT)+ 1 |
0 ε>μ (=εF) のとき |
このステップの境界を与えている,絶対零度 T=0 での化学ポテンシャルμ=εF をフェルミエネルギーといいます。つまり,絶対零度では,フェルミエネルギーより低いエネルギー準位には100
%粒子が占有しており,フェルミエネルギーより高いエネルギー準位には粒子が全く占有していません。したがって,絶対零度における自由粒子の粒子数,エネルギーは,(2.168),(2.169) 式は,積分範囲 ( 0〜εF) において,
fF(ε) =1
とすることができ,
| N =2πgV |
 |
2m |
 |
3/2 |
|
 |
εF |
|
|
 |
ε |
|
dε |
|
|
|
| h2 |
|
0 |
| E =2πgV |
 |
2m |
 |
3/2 |
|
 |
εF |
|
|
|
 |
ε |
ε |
|
dε |
|
|
|
| h2 |
|
0 |
によって計算できます。そして積分結果は,
| N = |
4πgV |
 |
2mεF |
 |
3/2 |
(2.201) |
|
|
|
| 3 |
h2 |
|
| E = |
4πgV |
 |
2mεF |
 |
3/2 |
εF |
|
|
|
| 5 |
h2 |
|
となります。これより内部エネルギーは,
ただし,εF は,(2.201) 式をεF で解いて,
| εF= |
h2 |
 |
3N |
 |
2/3 |
= |
h2 |
 |
3ρ |
 |
2/3 |
|
|
|
|
|
|
|
|
| 2m |
4πgV |
|
2m |
4πg |
|
| = |
h2 |
 |
6π2ρ |
 |
2/3 |
[フェルミエネルギー] |
|
|
|
| 2m |
g |
|
で与えられます。ここで,h = h/2π です。さらに,
| kF= |
 |
6π2N |
 |
1/3 |
= |
 |
6π2ρ |
 |
1/3 |
[フェルミ波数] |
|
|
|
|
| gV |
|
g |
|
と定義します。さらにフェルミ温度がεF/k で定義されますが,それはフェルミエネルギーより,
| εF= |
h2 |
 |
3N |
 |
2/3 |
= |
h2 |
 |
3ρ |
 |
2/3 |
|
|
|
|
|
|
|
|
| 2mk |
4πgV |
|
2mk |
4πg |
|
| = |
h2 |
 |
6π2ρ |
 |
2/3 |
[フェルミ温度] |
|
|
|
| 2mk |
g |
|
となります。
一方,絶対零度ではエントロピーは,S=0 です。よって,ヘルムホルツ自由エネルギーは,
F = E−TS
さらに,絶対零度では,μ=εF であることに注意して,グランドポテンシャルは,
| J = F −μN=− |
2 |
NεF [T=0] |
|
| 5 |
↓ N について,(2.201) 式を代入
| E =− |
2 |
|
4πgV |
 |
2mεF |
 |
3/2 |
εF |
|
|
|
|
| 5 |
3 |
h2 |
|
↓ εF= μ (T = 0 にて)
| E =− |
8πgV |
 |
2m |
 |
3/2 |
μ5/2 (2.209) |
|
|
|
| 15 |
h2 |
|
また,圧力は,
| P =− |
J |
= |
2NεF |
= |
 |
= |
2E |
 |
|
|
|
| V |
5V |
3V |
| = |
2 |
ρ |
h2 |
|
 |
|
3ρ |
 |
3/2 |
[T = 0] (2.210) |
|
|
|
|
| 5 |
2m |
4gπ |
|
で与えられます。つまり,絶対零度においても理想フェルミ気体の圧力はゼロとはなりません。フェルミ粒子は運動とは関係なく,見かけ上の斥力が働いていてお互いを避けるように振る舞うことが分かります。
そして,ρ の1次に比例する修正古典理想気体の圧力に対して,フェルミ理想気体ではρは
5/3 に比例するため,密度の増加につれて,より急激に圧力が上昇していくことも分かります。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
4. 熱力学関数の近似解
最近では,パソコンでも簡単に数値計算することができるのですが,物理的な意味を掘り下げるために特殊関数の積分を近似して,初等関数で表す方法も示しておきます。
- 高温近似 -
T >> TF,すなわち,ξ << 1 の場合の近似方法は,
f (n, ξ) ≒ ξ [高温近似]
(2.211)
とします。このとき,最初に求めたフェルミ-ディラック積分を用いたフェルミ気体に関する熱力学量が修正古典理想気体のものと一致することが確認できます。主要な熱力学関数について具体的な近似計算結果を一覧に示します。

- 低温近似 -
次に低温近似です。低温とは,T << TF のことですが,TF の典型的な値は下記のとおり,104 〜105K オーダーで室温よりずっと高温です。

したがって,一般的材料が利用される環境は低温とみなすことができるわけで,数値計算しかできない特殊関数を避け,統計熱力学的な諸量を初等関数で近似して示しておくことは大変有用です。そのためには次のフェルミ-ディラック積分の展開公式を用います。
いくつか具体例を書いておきます。
まず,粒子数 N の (2.180) 式にこの展開式の第2項まで用いると,
| = |
gV |
|
4 |
(logξ)3/2 |
 |
1+ |
π2 |
|
1 |
|
 |
|
|
|
|
| λ(T)3 |
|
|
|
|
| 3 |
 |
π |
|
|
8 |
(logξ)2 |
|
|
|
|
| ↓ λ(T) = h/ |
 |
2πmkT |
を代入して変形 |
|
3N |
 |
h2 |
 |
3/2 |
|
=(kT logξ)3/2 |
 |
1+ |
π2 |
|
1 |
|
 |
|
|
|
|
|
| 4πgV |
2m |
|
8 |
(logξ)2 |
| ↓ εF= |
h2 |
 |
3N |
 |
2/3 |
|
|
|
|
| 2m |
4πgV |
|
| εF3/2 |
=(kT logξ)3/2 |
 |
1+ |
π2 |
|
1 |
|
 |
|
|
| 8 |
(logξ)2 |
書き直して,
| ≒εF3/2 |
 |
1− |
π2 |
|
1 |
|
 |
|
|
| 8 |
(logξ)2 |
これより,化学ポテンシャルμは,
μ=kT logξ
| ≒εF |
 |
1− |
π2 |
|
 |
2/3 |
|
| 8 (logξ)2 |
| ≒εF |
 |
1− |
2 |
|
π2 |
|
 |
|
|
| 3 |
8(logξ)2 |
| ≒εF |
 |
1− |
π2 |
 |
kT |
 |
2 |
 |
(2.219) |
|
|
| 12 |
εF |
| =εF |
 |
1− |
π2 |
 |
T |
 |
2 |
 |
[低温近似 T << TF] |
|
|
| 12 |
TF |
すなわち,低温 (T << TF) での化学ポテンシャルのフェルミエネルギーからのずれは,温度の2 乗に比例して低下することが分かります。
次に内部エネルギーです。(2.183)より,
| E = |
3 |
NkT |
f (5/2, ξ ) |
|
|
|
| 2 |
f (3/2, ξ ) |
| = |
3 |
NkT |
|
| 8 |
|
|
|
|
| 15 |
 |
π |
|
|
(kT logξ) |
|
|
|
|
|
| 2 |
| 4 |
|
|
|
|
|
| 3 |
 |
π |
|
|
|
|
| ≒ |
3N |
(kT logξ) |
 |
1+ |
5π2 |
|
1 |
 |
 |
1− |
π2 |
|
1 |
|
 |
|
|
|
|
|
| 5 |
8 |
(logξ)2 |
8 |
(logξ)2 |
| ≒ |
3N |
(kT logξ) |
 |
1+ |
π2 |
|
1 |
|
 |
|
|
|
| 5 |
2 |
(logξ)2 |
ここで,上式の (kT log ξ ) に低温近似の化学ポテンシャル (2.219) 式を代入すると,
| ≒ |
3N |
εF |
 |
1− |
π2 |
 |
kT |
 |
2 |
 |
 |
1+ |
π2 |
|
 |
kT |
 |
2 |
|
 |
|
|
|
|
|
| 5 |
12 |
εF |
2 |
εF |
| ≒ |
3NεF |
|
 |
1+ |
5π2 |
 |
kT |
 |
2 |
|
 |
|
|
|
| 5 |
12 |
εF |
分母にあるεF だけ kTF と書き直せば,
| E ≒ |
3NεF |
|
 |
1+ |
5π2 |
 |
T |
 |
2 |
 |
[低温近似 T << TF] |
|
|
|
| 5 |
12 |
TF |
が得られます。
比熱はこれを T で微分して,
| Cv= |
 |
∂E |
 |
V,N |
=Nk |
π2 |
 |
T |
 |
|
|
[低温近似] |
|
|
|
| ∂T |
2 |
TF |
このようにフェルミ気体の比熱は低温で温度に比例することを示しています。フェルミ理想気体は金属の自由電子ののモデルとされますが,格子比熱の影響の少ない低温領域で,金属の比熱が温度に比例していることをよく説明しています。
同様に圧力は,E = (3/2)PV より,
| P ≒ |
2NεF |
|
 |
1+ |
5π2 |
 |
T |
 |
2 |
 |
[低温近似] |
|
|
|
| 5V |
12 |
TF |
となります。
J =−PV よりグランドポテンシャルは直ちに求まります。
エントロピーは,一般式 (2.195) を低温近似で展開しても求めてもよいですが,これまでに導いた値を用いて,(E−J −μN)/T を計算してもよいでしょう。
ヘルムホルツエネルギーは F = E−TS より計算します。
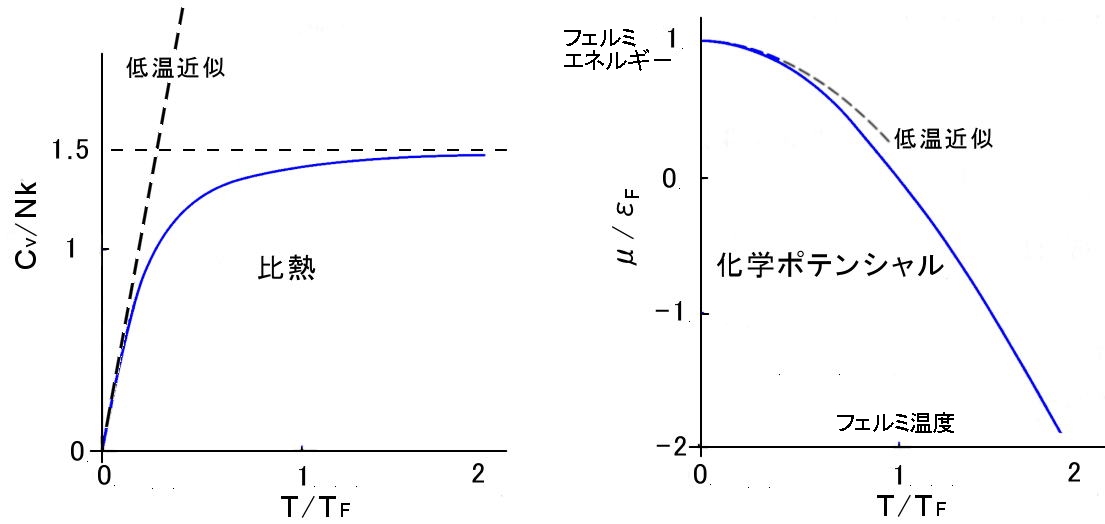
最後,ここで得た結果を以下の表にまとめておきましょう。比熱,化学ポテンシャルについては,下図にグラフを示しました
 |
|
理想フェルミ気体の比熱と化学ポテンシャルの温度依存性。
|
[目次]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
Ξjf フェルミ粒子の大分配関数 (2.160)
![]() を積分に置き換えると,
を積分に置き換えると,
