| t112 統計性:量子統計と古典統計 | |
| f-denshj.com 更新日: 21/12/10 5. を追加 | |
| サイト検索 | |
| 目次へ | |
量子力学の教えるところ[#]では,系の状態を表す波動関数は,(局在していない)区別のつかない同種類の粒子の交換に対して対称関数であるか反対称関数[#]であるかのどちらかでなければいけません。この性質をきちんと反映した統計力学を量子統計といいます。前者に従う粒子は,多数の粒子が同じ状態をとることができるボ−ス粒子(=ボソン),後者に従う粒子は,同じ状態をとれる粒子は1つまでに限られるフェルミ粒子(=フェルミオン)です。厳密に言えば,自然界のすべての粒子は量子統計(=ボース-アインシュタイン(BE)分布とフェルミディラック(FD)分布)に従うわけですが,古典統計において,局在していない同種の粒子は区別が付かないという理由から並び替えの順列数N!で割って状態数を修正する,いわゆる修正古典統計も適当な条件下では十分成立します。
[1] ここではこれらの分布をグランドカノニカルアンサンブルにおける大分配関数を用いて,縮退のない場合について考えます。まず,1粒子固有状態に通し番号 j を付け,それら1粒子固有状態のエネルギー固有値εj とします。ここで,注意すべきは,番号 j は,「系の微視的状態」ではなく,また,粒子に付けられているのでもなく,「1粒子がとりうる固有状態(とりあえず,電子が収納される原子軌道をイメージすればよい)に付けられている」 ということです。ただし,ここでは簡単のためエネルギー縮退はないとします。また,j の上限は無限とし,系は粒子数無限とみなせる熱粒子浴と接触して熱平衡状態にあるグランドカノニカルアンサンブルとします。
すると,多数の粒子からなる系全体の微視的状態 r は1粒子エネルギー固有状態εj にある粒子数を nj をj=1から最大数まですべて指定してやることで表すことができます(下表)。
微視的状態 r 1粒子エネルギー固有値
εjε1 ε2 ・・・ εjにある粒子数
njn1 n2 ・・・
この微視的状態 r をベクトルのように,
q =(n1,n2,n3,・・・・・・) [粒子数表示]
と書くことにすれば,
微視的状態 1 (0,0,0,・・・・・・) ← 粒子がまったくない状態
微視的状態 2 (1,0,0,・・・・・・) ←ε1に1個粒子がある状態
微視的状態 3 (0,3,0,・・・・・・) ←ε2に3個粒子がある状態
:
微視的状態 r (n1,n2,・・・) ←ε1にn1個,ε2にn2個,・・・粒子がある状態
:
というようになります。この表示方法を粒子数表示といいます。
[2] このようにqを指定すれば,系が状態 r にあるときの粒子数NrとエネルギーErが次のように一意的に定まることもわかります。
Er = njεj= n1ε1+n2ε2+・・・
Nr = nj =n1 + n2 +・・・
そこで,大分配関数,
Ξ = exp Nrμ−Er kT
を考えますが,ここで,「すべての可能な微視的状態」にわたる和を意味する![]() は,数表示qを用いると,次のように書き換えることが可能です。
は,数表示qを用いると,次のように書き換えることが可能です。
exp Nrμ−Er = exp{-β( n1(ε1−μ)+n2(ε2−μ)+・・・)} kT
ここで,大分配関数ではNrについては0から∞までいかなる値をとってもかまわないことから,各njについても,それらの部分和,n1+n2+・・+nj に制限はなく,他のni (i≠j) の値を気にすることなく自由に和を取れば良いと考えることができます。すなわち,q=(n1,n2,・・・,nj,・・・)におけるnjを独立に[#],それぞれが0から∞まで変化させて,あらゆる組み合わせについて考えればよいことになります。
[3] ところが,冒頭で述べた量子力学的な要請(量子統計)[#]から,1つのエネルギー固有状態に入る粒子数 nj について次のような2とおりがあります。
(1) 0 または 1 をとる [フェルミ統計]
(2) 0,1,・・・,∞ をとる [ボース統計]
つまり,nj が0から∞まで自由に取り得ると考えて良いのはボース粒子の場合だけで,フェルミ粒子の場合は,0か1しかとることができません。ただし,その並びは自由です。これを記号で表せば,微視的状態すべてにわたる和を意味する![]() は次のように2つのケースに分けて考えればよいことになります。
は次のように2つのケースに分けて考えればよいことになります。
(1) ≡ 1 1 ・・・・ 1 [フェルミ統計の場合] Σ Σ Σ n1=0 n2=0 n∞=0
(2) ≡ ∞ ∞ ・・・・ ∞ [ボース統計の場合] Σ Σ Σ n1=0 n2=0 n∞=0
これより,大分配関数はそれぞれ,
(1)フェルミ粒子の場合:
↓ 各nj について独立に和をとって,
Ξフェルミ = 1 1 exp{-β( n1(ε1−μ)+n2(ε2−μ)+・・・)} Σ ・・ Σ n1=0 n∞=0
= 1 1 exp{-βn2(ε2−μ)+・・・)} × ・・・ Σ exp{-βn1(ε1−μ)} × Σ n1=0 n2=0
={1+exp{-β(ε1−μ)}} × {1+exp{-β(ε2−μ)}} × ・・・
= ∞ {1+exp{-β(εj−μ)}} Π j=1
≡ ∞ Ξjフェルミ Π j=1
ただし, Ξjフェルミ ≡ 1+exp{-β(εj−μ)}
(2)ボース粒子の場合:
Ξボース= ∞ ∞ exp{-β( n1(ε1−μ)+n2(ε2−μ)+・・・)} Σ ・・ Σ n1=0 n∞=0
↓ 各njが独立
= ∞ exp{-β( n1(ε1−μ)}× ∞ exp{-β(n2(ε2−μ)}×・・・・・ Σ Σ n1=0 n2=0
↓ exp{-βn1(ε1−μ)}=[exp{-β (ε1−μ)}]n1 に注意して
={1+exp{-β(ε1−μ)}+[exp{-β(ε1−μ)}]2+・・・}
×{1+exp{-β(ε2−μ)}+[exp{-β(ε2−μ)}]2+・・・・}
× ・・・
↓ 等比級数の公式 1+X+X2+・・・ = 1/(1−X)
= 1 × 1 × ・・・ 1−exp{-β(ε1−μ)} 1−exp{-β(ε2−μ)}
=
∞ Π j=1 1 1−exp{-β(εj−μ)}
≡ ∞ Ξjボース Π j=1
ただし, Ξjボース ≡ 1 1−exp{-β(εj−μ)}
と計算することができます。
ここで途中の等比級数の収束条件をきちんと書いておくと,exp{-β(εj−μ)}<1,すなわち,
μ < εj ボース粒子に課せられる条件
を明記しておきましょう。一番小さいエネルギ−固有値が0であるときは,この条件はμ<0 と読み替えることになります。
[1] これらからただちにエネルギー準位に縮退のないときのグランドポテンシャル J=−kTlogΞ は,
J =−kT log {1+exp{-β(εj−μ)}} フェルミ
J =+kT log {1−exp{-β(εj−μ)}} ボース
と得られます。 (ただし,β=1/kT)
一方,1粒子エネルギー固有状態 j にある粒子数の期待値,<nj>,占有数(フェルミ分布の場合は占有確率ともみなせる)は,グランドカノニカルアンサンブル方法のところ[#]で導いた公式,
N(T,V,μ)=− ∂J = <nj>f またはb ∂μ T,V
ここで,
<nj>f≡kT ∂logΞjフェルミ = exp{-β(εj−μ)} = 1 ∂μ T,V 1+exp{-β(εj−μ)} exp{β(εj−μ)}+1
= 1 [フェルミ粒子] exp{(εj−μ)/kT}+1
および,
<nj>b≡kT ∂logΞjボース = exp{-β(εj−μ)} = 1 ∂μ T,V 1−exp{-β(εj−μ)} exp{β(εj−μ)}−1
= 1 [ボース粒子] exp{(εj−μ)/kT}−1
と求まります。そして,<nj>f,<nj>bを各準位にわたる総和をとると,系の全粒子数の期待値を与え,
<N>= <nj>f,またはb= 1 exp{(εj−μ)/kT}±1
となります。
[2] これら分布関数は,フェルミ粒子に対して,フェルミ-ディラック分布関数(=フェルミ分布),ボース粒子に対して,ボース-アインシュタイン分布関数(=ボース分布)と名前が付けられています。
分布関数
f(εj)=<nj>= 1 +: フェルミ(-ディラック)分布関数 exp{(εj−μ)/kT}±1 −: ボース(-アインシュタイン)分布関数
エネルギー固有値が連続的に分布しているとみなさる極限では,j を省いてf(ε)と書きますが,(正確にはf(ε,μ,T) )
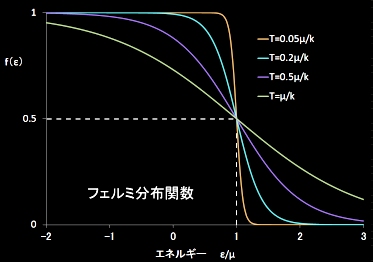
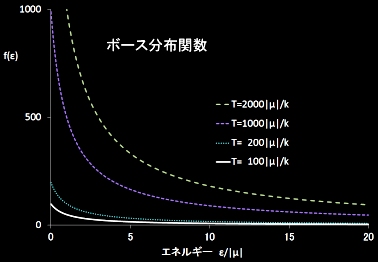
そのときの各温度における各分布関数(連続極限)を示すと下図のとおりとなります。
 |
 |
|
| フェルミ-D分布 | ボース-E分布(μは負の値) |
どちらもεに関して単調な減少関数ですが,フェルミ-ディラック分布(上図左)では,f(ε=μ)=1/2の定点を通り,温度が低温になるにつれて,絶対零度で実現するステップ関数[#]に近づいていく様子が見てとれます。そして,絶対零度においては,ε<μの準位では,f(ε)=1,ε>μの準位では,f(ε)=0となり,粒子は低い準位に隙間なくぎっしりと詰まった状態となります。この境界ε=μをフェルミ準位といいます。
一方,ボースアインシュタイン分布(上図右)は,粒子数に制限がないために比較的高温では,1を超えていくらでも大きな値をとることができます。この分布は,T→0,μ
→−0 における極限では,f(0)=∞,f(ε)=0 (ε>0) という恐ろしく端だけが尖がった関数になりますが,これはN=∞などの近似を用いたためで,正確には,この極限ではすべての粒子が最低準位に詰まった状態が実現します。きちんとした取り扱いはボースアインシュタイン凝縮のところで説明しますので,ここでは深入りしません。
今度はエネルギー準位に縮退がある場合のフェルミ−ディラック分布とボース−アインシュタイン分布を2.とは異なる方法で導出します。
[1] 繰り返しになりますが,量子力学の導入が必要な状況では,
(1) 1つの量子状態を占有できるのはただ一つの粒子だけ⇒フェルミ−ディラック統計
(2) 1つの量子状態を占有できる粒子数には制限がない⇒ボース-アインシュタイン統計
の2通りの統計性(=量子状態数の数え方)があります。(1)は原子や分子軌道に入っている電子について述べたパウリの排他原理の形でよく知られてます。もう一つの(2)に従う粒子の代表はHe4原子で,その低温での挙動がしばしば引き合いに出されます。
ここでは,波動関数の対称性,スピン統計については詳述しません。
量子統計 (全)波動関数 スピン フェルミ−ディラック統計 フェルミオン 反対称 半整数スピン ボース-アインシュタイン統計 ボソン 対称 整数スピン
[2] ここではこれらの統計性(規則)の違いで系の状態数の計算にどのような違いが現れるのか見ていきましょう。
右図のようなエネルギーがε1,ε2,・・・εj,・・・ となる準位を考えて,そこへ合計 N 個の粒子を系の全エネルギーが E であるように配分する仕方の数を状態数として数えることにします。ただし,エネルギー ε1,ε2,・・・εj,・・・ の準位はそれぞれ,Δ1,Δ2,・・・Δj,・・・ 個 の固有状態(=縮退)をもっているとします。 (下図参照)
(1) そこで,j 番目の準位に,フェルミ統計にしたがってnj 個の粒子を収納する仕方は,Δj 個の状態に重複を許さずに nj 個の粒子を配分する仕方(⇔ Δj個の状態の中から粒子を収容するnj個の状態を選び出す組合せ)に等しく,
ΔjCnj= Δj (Δj−nj)!nj!
がこの準位が関係する状態の数となります。
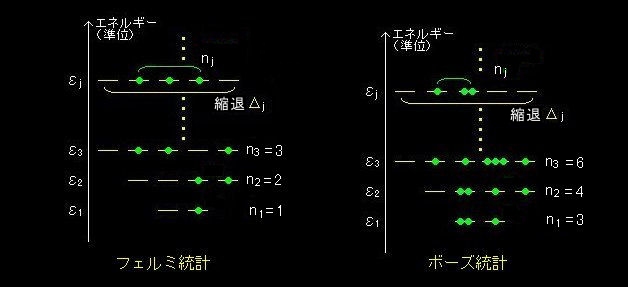
一方,ボース統計に従う場合は,Δj 個の状態へ重複を許して nj 個の粒子を配分する仕方(⇔ Δj個の状態の中から粒子を収容するnj個の状態を重複を許して選び出す組合せ),
ΔjHnj=Δj+nj−1Cnj= (Δj+nj−1)! (Δj−1)!nj!
が状態の数となります。 重複組み合わせについては,⇒[#]
(2) これらをすべてのエネルギー準位 j = 1,2,3,・・・ について求めて,それらを掛け合わせた数が系の全状態数となります。すなわち,各統計性のもとで, q*= ( n1,n2,・・・nj, ・・・ ) と表記する分布(=粒子の占有状態):
ε1 に n1 個
ε2 に n2 個
:
:
εj に nj 個
:
にあるときの系の量子力学状態数は,
W (n1,n2,・・,nj, ・・ ) = Δj [フェルミ統計による状態数] ・・・[*f] (Δj−nj)!nj!
W (n1,n2,・・,nj, ・・ ) = (Δj+nj−1)! [ボース統計による状態数] ・・・[*b] (Δj−1)!nj!
と数えられることになります。
cf.
W(n1,n2,・・,nj, ・・ ) = (Δj)nj [ボルツマン統計(修正古典)による状態数] nj!
[1] N個の粒子がエネルギー:ε1(状態数Δ1),ε2(状態数Δ2),・・・εj(状態数Δj),・・・ のいずれか状態にn1,n2,・・,nj, ・・個ずつ配分され,系のエネルギーが E として与えられている状況を考えます。すなわち,条件,
N = nj ・・・・・(1)
E = εjnj ・・・・・(2)
が課せられているとします。このとき,1.で求めた状態数 W (n1,n2,・・,nj, ・・ ) を最大にする分布 q*=(n*1,n*2,・・,n*j, ・・ ) (=最大確率分布 ) が実際に観測される分布となります。
[2] 今,解くべき数学としての問題は,条件(1),(2)のもとで [*f] ,[*b] の極値を求める条件付極値問題で,これはラグランジュの未定乗数(未定係数)法[#]で解くことができます。ただし,数学的な取り扱いやすさから,W (n1,n2,・・,nj, ・・ ) の代わりに log W (n1,n2,・・,nj, ・・ ) について計算します。もちろん,極大を与える分布q*は対数をとっても計算しても変わりありません。
フェルミ-ディラック分布の導出
まず, [*f]において,log W を n が大きな数のときに成り立つスターリングの公式 log n!=n log n−n を用いて近似すると,
log W = log Δj (Δj−nj)!nj!
≒ Δj log Δj − (Δj−nj)log(Δj−nj)− nj log nj ・・・ [*f]’
ラグランジュの未定係数法 [#] を適用するために,これらの変分をとると,
δ( log W ≒ log Δj−nj δnj ・・・ [*1] nj
さらに,
δnj = 0 ・・・・・(1)’
εjδnj = 0 ・・・・・(2)’
の2式にα,βを未定乗数として, [*1]−α×(1)’−β×(2)’= 0, すなわち,
log Δj−nj −α−βεj δnj = 0 nj
が任意のδnj について成り立つことが必要です。そのためには,( ) の中がすべてのj に対して 0 であることが必要です。 すなわち,各jに対して,
log Δj−nj −α−βεj = 0 ⇔ Δj−nj =eα+βεj nj nj
これをnj についてとき,最大確率分布を与えるようなnj という意味で,n*j と記号を改めると,
n*j = Δj ; j = 1,2, ・・・・・ eα+βεj+1
となります。( j はエネルギー準位に対して付けられていることに注意せよ。 粒子でも,微視的状態に対してでもない。)
ボース-アイシュタイン分布の導出
ボース・アイシュタイン統計の導出も符号が一部異なるだけで同様にできます。
スターリングの公式,および,Δj+nj−1≒Δj+nj の下で, ←
log W = (Δj+nj−1)! (Δj−1)!nj!
≒ (Δj+nj) log (Δj+nj) − Δjlog Δj − nj log nj ・・・[*b]’
ラグランジュの未定係数法 [#] を適用するために,
δ( log W ) ≒ Δj+nj δnj ・・・・ [*2] nj
δnj = 0 ・・・・・(1)’
εjδnj = 0 ・・・・・・(2)’
の2式にα,βを未定乗数として, [*2]−α×(1)’−β×(2)’= 0, すなわち,(FD分布のときと同じα,βという記号を用いてますが,紛れはないでしょう。実際に共通の物理的意味をもつことが判明するわけですし,・・)
log Δj+nj −α−βεj δnj = 0 nj
log Δj+nj −α−βεj = 0 ⇔ Δj+n*j =eα+βεj nj n*j
これを n*j について解いて,
n*j = Δj ; j = 1,2, ・・・・・ eα+βεj−1
以上,2つの量子統計の結果をまとめると,
n*j = Δj ; j = 1,2, ・・・ [フェルミ・ディラック分布] eα+βεj+1 n*j = Δj ; j = 1,2, ・・・ [ボース・アインシュタイン分布] eα+βεj−1
このq*=(n*1,n*2,・・,n*j, ・・・ ) が各統計における最大確率分布で,フェルミ-ディラック分布,ボース-アインシュタイン分布と呼ばれます。
n*j = Δj =Δj exp(−α−βεj ) [ボルツマン分布] eα+βεj
α,βのとるべき値については,フェルミ分布であれば,[*1]式中[#]でデルタをdという記号に変えて,
1 dS =d( log W ) ≒ k
= log Δj−nj dnj nj
= (α+βεj )dnj
= αdn+βdE
と変形して,熱力学公式,(ここでVは一定と考える。)
∂S = 1 および, ∂S =− μ ∂U V,N T ∂N U,V T
を思い出して[#],ここで導いた結果との整合性を要求すると,
β= 1 および, α=− μ kT kT
でなければならないことが分かります。ボース分布についても同様にパラメータを決定できます。
まとめると,(n*j =<nj>f またはn*j =<nj>bと考えてよい。)
(証明は省略するが,古典統計分布は上式の分母の±1を0とすればよい。)
( j はエネルギー準位に対して付けられていることに注意せよ。 粒子でも,微視的状態に対してでもない。)
n*j = Δj [フェルミ・ディラック分布] ; j = 1,2, ・・・・・ exp{(εj−μ)/kT}+1 n*j = Δj [ボース・アインシュタイン分布] ; j = 1,2, ・・・・・ exp{(εj−μ)/kT}−1
したがって,フェルミ・ディラック分布の場合,系の全粒子数は,
<N>= n*j = Δj exp{(εj−μ)/kT}+1
で得られます。これを積分で近似する場合は,
<N>= gD(ε) dε [フェルミ・ディラック統計] exp{(ε−μ)/kT}+1
と表記できます。 gはスピンを考慮するときも考えて付加しました。
なお,離散的な準位を持つ場合も,クロネッカーのデルタ関数[#]を用いて,
D(ε)= Δjδ(ε−εj)
とすれば,積分表記の中に含めることができます。
ボース・アインシュタイン分布を連続関数として積分表示する場合は,特別な注意が必要なので,ボース理想気体を参照してください。
[1] N 個の同一種類の自由粒子からなる系の古典統計の分配関数は,1 粒子に対する分配関数をN 乗して,配置数N ! で割った,
Z (T, V, N) = 1 exp (-βεj)N= 1 Z (T, V, 1)N N ! N !
ただし,
Z (T, V, 1) = z1 =
exp (-βεj ) [1 粒子分配関数]
で与えられます(修正古典統計)。これより,大分配関数は絶対活量ξ≡eμ/kT を用いて,
Ξ(T, V, μ) =![]() ξN Z (T, V, N)
ξN Z (T, V, N)
= 1 (ξ Z (T, V, 1))N N !
↓ 公式: ex=1+ 1 ・x+ 1 ・x2+・・・+ 1 ・xn+ 1! 2! n!
= exp {ξ Z (T, V, 1)}
= exp {ξ exp (-βεj ) }
=exp { exp (β(μ−εj )) }
ここで,
Ξj c = exp [exp (β(μ−εj ))]
とおきます。
[2] これより,グランドポテンシャルは,
J = - kT log Ξ = - kT log
exp [ exp {β(μ−εj )}]
= - kTexp [ -β(εj −μ)]
および,分布関数は,
<nj >c ≡kT ∂log Ξjc = exp {β(μ−εj )} ∂μ T,V
= 1 [古典統計] (2.149) exp [β(εj−μ)]
系の全粒子数は,
<N>c =
<nj>c
= 1 [古典統計] (2.150) exp [β(εj−μ)]
これは量子統計において,(εj−μ)/kT >> 1 であるときの近似となっています。縮退があるときも含めて3つの統計をまとめると,表2.3 のようになります。

[3] これらは1 粒子エネルギーが離散的な場合の表記ですが,連続的とみなす場合は,修正古典統計の場合であれば,全粒子数 (2.150) 式は,
Δj [離散] ⇒ D(ε) dε [連続] (2.151) exp [β(εj−μ)] exp [β(ε−μ)]
なお,系が離散的なエネルギー準位を持つ場合も, クロネッカーのデルタを用いて,
D(ε) =
Δjδ(ε−εj ) [離散]
とすれば,積分表記で離散状態を扱うこともできます。
[4] では,連続的な状態密度で表される古典理想気体の場合に (2.151) 式を適用してみましょう。そのために状態密度を,
D(ε) =2πV 2m 3/2
ε h2
とすればよい [#] ので,積分表示では,exp (βμ)≡ξ と表記して,
N =2πV 2m 3/2
ε dε h2 ξ-1exp {ε/kT}
E =2πV 2m 3/2
ε ε dε h2 ξ-1exp {ε/kT}
となります。この積分を実行すると,
N =2πV 2m 3/2 ξ
ε exp {−ε/kT} dε h2
=2πV 2m 3/2 ξ×(kT)3/2
π h2 2
=V 2πmkT 3/2 ξ h2
= Vξ (2.156) λ(T)3
および
E =2πV 2m 3/2 ξ
ε εexp {−ε/kT} dε h2 ↓ 積分公式
=2πV 2m 3/2 ξ×(kT)5/2
3 π h2 4
=V 2πmkT 3/2 ξkT× 3 h2 2
= 3Vξ kT = 3 NkT (2.157) 2λ(T)3 2
となります。なお,(2.156),(2.157) 式の導出の途中,積分公式
xnexp (-ax)= Γ(n+1) an+1
を用いました。ここで,
Γ(3/2) =
π ,および, Γ(5/2) =
3 π 2 4
です。
SUSTAINABLE TOKIWADAIGAK SINCE 2002