|
６ 多変数関数の微分 | |
| f-denshi.com [目次] 最終更新日： 07/6/23 | ||
| サイト検索 | ||
最初に用語の簡単な説明をしておきます。微分積分の舞台(定義域）になるのは１変数の場合は実数の集合[#]です。しかし，変数が２つ以上の n変数関数の場合，それは n次元ユークリッド空間 と呼ばれるものになります。その定義は，
実数の集合 R のn 個の直積： R×R×･･･×R を n 次元ユークリッド空間という。
ここで，集合の直積 ( direct product )とは，３つの集合 A，B，C の場合で説明すれば，集合A から要素 a を，集合B からは要素 b を，集合C からは要素 c というように一つづつ取り出して，この要素を並べて，
( a,b,c ) ← これを直積集合の点 といいます。
と書き，これを新しい集合の要素とみなします。そして，このようにしてつくった要素全体からなる新しい集合を，集合 A，B，C の直積，または直積集合，直積空間 ともいい，
A×B×C ＝ {(a,b,c)｜a∈A，b∈B，c∈C}
書きます。 特に，A＝B＝C＝R(実数の集合) の場合の直積集合が３次元ユークリッド空間R3 です。さらにその任意の２つの元と実数 ，つまり，
r1＝( x1,y1,z1 )，r2 ＝( x2,y2,z2 ) ∈ R3，a ∈ R
に対して，”和”，”スカラー積” を
(１) r1＋r2 ＝ ( x1＋x2,y1＋y2,z1＋z2 ) ［和］
(２) ax1 ＝ ( ax1,ay1,az1 ) ［スカラー積］
のように定義したもの(３次元）ベクトル空間と呼びます。さらに詳しい「ベクトル」に関する用語は，ベクトル解析[#]，線形代数[#] を参照してもらうことにして，本題の多変数関数の解析学の話に進みましょう。
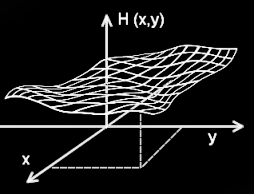［１］ 定義域が複数の実数の組，すなわち，n次元ユークリッド空間である関数を多変数関数と言います。変数の数は形式的にいくらでも増していくことができますが，われわれは時間を備えた３次元空間の中に存在しているということから，応用上，２変数から４変数関数までの場合が特に重要です。
具体例を挙げておくと，２つの変数 x，y で指定される場所における標高(＝高さ) H を対応させて地形を表現する場合があります。これは数学的には，定義域が２次元の平面，値域が１次元の直線であるような２変数関数，
Ｈ(x,y)
を考えることになります。もちろん，地球が丸いとか，定義域，値域が有限であるとか細かいことはとりあえず無視しての話。この定義をきちんと書くと，
|
定義 f ： (x,y) → w を２変数関数といい， w＝ｆ(x,y) と書く。 |
似たような問題として，時間とともに変動する水面の高さを記述するのであれば，３変数関数，
H(x,y,t)
を考えることになります。この場合，３つの変数 x，y，t は対等であることに注意してください。したがって，この３変数関数を図示するためには４つの座標軸が必要です！
［２］ 次に時間を媒介変数として含むような例を考えてみましょう。山中を歩きまわっている人がある時刻にどの標高にいるかを関数で示したいならは，それは合成関数によって，
H(t)＝H(x(t),y(t))＝H(r (t)) ； r (t)＝(x(t),y(t))
を考えることになります。つまり，ある時刻での人が立っている２次元上の位置 r (t) がわかれば，自動的に位置の関数である標高もわかるという場合です。これを，z=H(x,y) として，３次元座標上に図示すると，媒介変数t を用いた 3次元空間内の曲線として表されるでしょう。
以上，いずれの例も値域は一つの実数値でしたが，このような関数はスカラー関数と総称されることもあります。
［１］ n 次元ユークリッド空間 Rn上で定義されたn変数関数を考えます。表記を簡単にするために２変数関数の場合で話を進めますが，n変数の場合への拡張は容易に推測がつくものと思います。まず，２変数関数，f(x,y) が連続関数であることの定義は，
定義域R2上の任意の点 P(a,b）に近づく点列：
Q1，Q2，･･･，Qn，･･･
に対応する値域上の点列：
f(Q1)，f(Q2)，･･･，f(Qn)，･･･
が f(P) に収束するとき，「写像 f(x,y) は点P で連続である」とします。一行で書けば，
Qn(xn,yn) → P(a,b) ならば， ｆ(xn,yn) → ｆ(a,b)
［２］ 近づくということをもう少し厳密に言い換えると，
| P(a,b) と Q(a＋h,b＋k) との距離 d(P,Q)＝ |  |
h2＋k2 | を 0 に[#] 近づけたとき， |
と言い直せます。これは１次元のときの距離｜xn−a｜の拡張になっています。また，１次元の場合の閉区間，開区間[#]を２次元(２変数)以上の場合に拡張した概念は，
開区間 (１次元)→ 領域 (２次元以上も)
閉区間 (１次元)→ 閉領域 ( closed domain ) (２次元以上も)
と呼ばれます。領域には有界であるときとそうでないときがあります。以上を用い，１変数関数の場合[#]にならって，２変数関数の連続性を厳密に書くと，
| 連続関数の定義 (１) 領域Dで定義された関数 ｆ(x,y) が，点 P(a,b) で連続とは， 「どんな小さな ε をとっても，ある正数 δ が存在し， d(Q(x,y),P(a,b))＜δ ⇒ ｜ｆ(x,y)−ｆ(a,b)｜＜ε となる。」 ことである。 (２) また，関数 f(x,y) が領域D の任意の点で連続であるとき， 「f(x,y) は領域D 上で連続関数である。」 という。 |
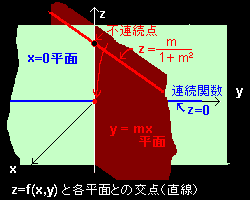［３］ 上の定義で注意すべきことは x，y が独立に変化してもよいので，Q が
P に近づく方向はあらゆる方向を考慮しなければならないことです。ある特定の方向，例えば，
| x方向： Q(x,b)→P(a,b) ⇒ ｆ(x,b)→ｆ(a,b) y方向： Q(a,y)→P(a,b) ⇒ ｆ(a,y)→ｆ(a,b) |
で連続であっても，関数f(x,y)として連続とは限りません。具体例を挙げておくと，関数，
f(x,y)＝
xy ： (x,y)≠(0,0) x2＋y2 0 ： (x,y)＝(0,0)
はx 軸，y 軸に沿っては原点において連続ですが，それから外れた，y＝mx，m≠0 にそっては，
f(x,mx)＝
m ： (x,y)≠(0,0) 1＋m2 0 ： (x,y)＝(0,0)
となり，原点で連続ではありません。
［４］ 連続多変数関数に関して重要な定理を一つ挙げておきます
| 定理 有界な閉領域で定義された連続関数は，有界で最大値，最小値をとる。 |
２変数関数の微分の定義です。これも１変数の微分の定義[#] の自然な拡張です。
| 定義 ある実数値 A，B が存在して，h，k → 0 のとき，２変数関数 f(x,y)について，
が成り立つとき，ｆ(x,y) は ( a,b ) で微分可能という(全微分可能ともいう)。 |
この定義は，3以上の任意のｎ変数の場合にも拡張されます。
そのとき，全微分可能な関数 f のとき，各変数の微小な変量が，dx，dy，dz，･･･ であるとき，f の変化量 df は，
df ＝ ∂f dx＋ ∂f dy ＋ ∂f dz ＋･･･ ∂x ∂y ∂z
と表すことができます。
また，１変数関数の時と同様な定理，
| 定理 ｆ(x,y)は (a,b) で全微分可能ならば，(a,b) で連続である。 |
が成り立ちます。証明は省略します。
蛇足ですが，微分係数を幾何学的なイメージで捉えるならば，関数がある点で微分可能連続であるとは，１変数の場合はその点で接線がただ一本存在することを言い，２変数関数の場合は，その点で接平面がただ一枚存在することをいっていると考えることができます。
それから，ついでに言っておくと，多変数関数の微分のことを全微分ということが多いのは，次章で述べる偏微分と区別するためです。方向微分係数 [#] なんていうのもあります。
