| 1 ベクトルの代数と公式 | |
| f-denshi.com [目次へ] 最終更新日:05/05/04 | |
| サイト検索 | |
この講義はベクトル解析の応用的な面 ( 電磁気学,(量子)力学など ) を理解する上の実践的な計算テクニックと知識の短期習得を主目的としています。ここでは代数に関する用語は高校の延長線上で理解できるよう配慮し,行列・ベクトル空間のきちんとした定義,演算規則等の体系的説明は,ときわ台学The講義:「連立1次方程式」,「線形代数入門」にあります。 一方,実数に関する微積分はときわ台学:「実数解析入門」を習得済みとして書いてます。つまり,実数解析学のつづきという位置づけ。
ベクトル解析に使われる用語の定義や表記法をまとめます。
[1] 任意の実数上の3次元ベクトルx は基底と呼ばれる1次独立な3つのベクトルの組:{u1,u2,u3}を定めると,
x =x1u1+x2u2+x3u3
と一意的に書くことができます。この基底ベクトルに係る係数を成分といい,しばしば,これを並べて,
x =(x1,x2,x3) [横ベクトル,または行ベクトル]
と書きます。つまり,ベクトルとは ”3個の実数の組” と考えることができます。これはまた,
x = x1 [縦ベクトル,または列ベクトル] x2 x3
のように縦に書くこともあります。成分がすべて実数のユークリッド空間 [#] の場合,行ベクトルと列ベクトルのどちらを採用するかは意味のないことです。しかし,行列とベクトルとの演算がかかわる場合,「行ベクトルは1行3列の行列,列ベクトルは3行1列の行列」として区別されます。なお,複素数を成分とするベクトルは固有値論入門で説明しています。また,ベクトルのn次元へ拡張は容易なので,ここでは原則的に3次元ベクトルで表記します。
[2] ベクトル値関数(またはベクトル関数)とは,次の写像,
写像: 変数(数 t,またはベクトルr = (x,y,z)) ⇒ ベクトル A = (A1,A2,A3)
をいいます。( ↑ ”数” を1次元ベクトルとみなせば,ベクトルからベクトルへの写像と一言でまとめることもできます。)
解析学で説明したC1写像もベクトル値関数です。ベクトル値関数の典型的なパターンは次のようになります。
| ベクトル値関数 (1) 1つの媒介変数t のベクトル値関数 (← t は時間を想定) A(t) = (A1(t),A2(t),A3(t)) = (A1,A2,A3) (2) 2つの媒介変数(u,v )のベクトル値関数 A(u,v) = (A1(u,v ),A2(u,v ),A3(u,v )) = (A1,A2,A3) (3) 3つの媒介変数(x,y,z)のベクトル値関数 (← (x,y,z)は空間座標を想定) A(x,y,z) =(A1(x,y,z),A2(x,y,z),A3(x,y,z)) = (A1,A2,A3) ( =A(r ) ) |
などがあります。(A1,A2,A3 ) が3次元ユークリッド空間の点 (x,y,z) を意味するとき,これを位置ベクトルといい,次の記号がしばしば用いられます。
r (x,y,z)=(x,y,z) (3次元空間内の点を表す)
これらがベクトル値関数(1),(2)のタイプである場合,
(1)' r =(x(t),y(t),z(t)) (3次元空間内の曲線を表す→[#])
(2)' r =(x(u,v),y(u,v),z(u,v)) (3次元空間内の曲面を表す→[#])
となります。ここで t が時刻である場合,(1)'は力学でいうところの質点の軌跡を表します。
一方,(3)のタイプは3次元空間のベクトル場と呼ばれ,その典型的な例としては,3次元空間内を定常的に流れる流体の速度分布 を表す,
(3)' v (r )=(v1(r ),v2(r ),v3(r ))
などがあります。
注意:
ときわ台学では,一般的なベクトルA の成分を,(Ax,Ay,Az)と書く表記は原則として用いません。
Axは「関数A のx に関する偏微分」と言う意味のために使い,ベクトル成分を示すときは,添え字 1,2,3 を用います。
[1] スカラーとは,いわゆる数(実数)で,λ,a,... などの記号(装飾のない文字)をしばしば使います。
[2] スカラー関数とは a を実数として,
写像: 変数(数 t,またはベクトルr ) → スカラー a
具体的には,
|
スカラー関数 |
ベクトル関数とスカラー関数の代数演算規則は,普通のスカラーとベクトルの場合[#]と同じです。ベクトル値関数を
A(t) = (A1(t),A2(t),A3(t)),B(t) = (B1(t),B2(t),B3(t)),スカラー関数を φ(t) として,
A(t)+B(t)=(A1(t)+B1(t),A2(t)+B2(t),A3(t)+B3(t))
φ(t)A(t) =(φ(t)A1(t),φ(t)A2(t),φ(t)A3(t))
などと定義します。スカラー関数については,解析学6章の多変数関数も参考にしてください。
[1] 3次元ベクトルの内積とは,2つのベクトル x ,y を一つの実数に対応させる写像で,次のように定義します。
| 内積 x ・y =(x,y )= |x ||y|cosθ : しばしば,内積の記号 ・ を省略して,xy とも書きます。 ここで,ベクトル x ,y の大きさ(=ノルム)を |x |,|y|,それらのなす角度をθとする。 |
内積の公理についてはこちら,⇒ [#]
注意 x (y・z )≠( x ・y )z ← よくやる間違い
ここでは,交換法則 x ・y =y ・x が成り立つことだけ強調しておきましょう。
[1] 3次元ベクトル空間の基底{u1,u2,u3}の各ベクトルが互いに 90°の角度をなし,大きさが1であるとき,すなわち,
us・ut = δst ← クロネッカーのデルタ [#]
を満たすならば,{u1,u2,u3}を正規直交基底といいます。特に,成分が 0 と 1 からなる3つのベクトル
e1=(1,0,0),e2=(0,1,0),e3=(0,0,1)
の組 {e1,e2,e3}を標準基底といいます。
[2] 正規直交基底を用いた3次元ベクトル空間の2つのベクトルの成分が,
x = (x1,x2,x3),y = (y1,y2,y3)
とするとき,
内積: (x,y )= x1y1+x2y2+x3y3
ノルム :|x|≡ (x,x ) = x12+x22+x32
余弦: cosθ = x ・y = x1y1+x2y2+x3y3 |x||y|
(x12+x22+x32)(y12+y22+y32)
と計算することができます。
SUSTAINABLE TOKIWADAIGAK SINCE 2002
[1] 外積の定義
3次元ユークリド空間で外積とは,2つのベクトルx,y から一つのベクトルz (=x ×y )への写像で,
| 外積 z =x ×y 大きさ: | z | =|x ×y |= |x ||y| sinθ, (x からy方向へ0≦θ≦π) 方向: x ,y の両方に垂直で,x ,y ,z の順で右手系になる。 ここで,ベクトル x ,y の大きさ(=ノルム)を |x |,|y|,それらのなす角度をθとする。 |
と定義します。正規直交座標系では,x = (x1,x2,x3),y= (y1,y2,y3)とすると,
z = (z1,z2,z3)
= x ×y
= (x2y3-x3y2 , x3y1-x1y3 ,x1y2-x2y1)
と成分で表すことができます。交代行列[#]を用いて,
z1 = 0 -x3 x2 y1 z2 x3 0 -x1 y2 z3 -x2 x1 0 y3
と書けることも重要です。
特に,標準基底ベクトル,e1,e2,e3 については,簡単な計算から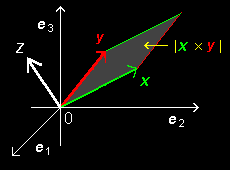
e1×e2 = e3
e2×e3 = e1
e3×e1 = e2・・・・・・・・・ [*]
の関係があることもわかります。また,
|x ×y |
はベクトル x ,y で作られる右のような平行四辺形の面積に等しくなります。
また,x ,y の座標成分をx → -x = (-x1,-x2,-x3),y → y= (-y1,-y2,-y3)のように反転させても,z → z となり不変です。このような性質を持つベクトルを擬ベクトル,または軸性ベクトルといいます。
[2] 外積の基本的な公式
| 公式1 外積
(1) x ×x =0 |
( 注意 ) x ×(y ×z ) ≠ (x ×y )×z
(1)-(4)[証明略]
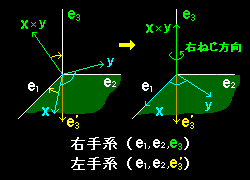 (5)は,x ×y (=z )はx ,y の張る平面に垂直なことを意味しています。3次元ユークリッド空間を考えるときは,その幾何学的方向は2とおり(x-y平面の表方向と裏方向)の定義が可能ですが,慣用では右手系と呼ばれる方を採用(定義)します(右図参照)。
(5)は,x ×y (=z )はx ,y の張る平面に垂直なことを意味しています。3次元ユークリッド空間を考えるときは,その幾何学的方向は2とおり(x-y平面の表方向と裏方向)の定義が可能ですが,慣用では右手系と呼ばれる方を採用(定義)します(右図参照)。
[3] 先程示したように,標準基底ベクトルにはe1×e2 =e3 という関係があります(つまり,右手系)。ここで,標準基底(縦ベクトル)の成分を横に並べた行列を考える[#]と,それは単位行列でその行列式は正です。
|e1e2e3| = 1 0 0 = 1 > 0 0 1 0 0 0 1
すると,左手系の標準基底ベクトルは,
e'1=(1,0,0),e'2=(0,1,0),e'3=-e3=(0,0,-1)
となり,|e1'e2'e3'|= -1 < 0 であることがわかります。
[4] 三重積
よく使われる公式です。
|
公式2 三重積 など (1) x ×(y ×z )=(x ・z )y -(x ・y )z [ベクトル3重積] (2) x ・(y×z )=y ・(z ×x )=z ・(x ×y ) ≡ [x y z ] [スカラー3重積] (εijk xi yjzk) (2)' [x y z ]=[y z x ]=[z x y ]=-[x z y ]=-[z y x ]=-[y x z ] (3) x ×(y ×z )+y ×(z ×x )+z ×(x ×y ) = 0 [ヤコビの恒等式] (4) (x ×y )・(z ×v ) =(x ・z )(y ・v )-(y ・z )(x ・v ) (4)' (x ×y )・(z ×v ) =x ・(y ×(z ×v )) (5) (x ×y )×(z ×v ) = [x y v ]z -[x y z ]v (6) (x ×y )・(y ×z ) ×(z ×x ) = [x y z]2 |
(証明略)
注意:
しばしば,内積と外積が混じりあう式は,「計算が可能な順に計算すること」との暗黙の了解がなされます。例えば,
x ・y ×z は,
x ・(y ×z ) は計算できるのでOKですが,
(x ・y )×z はスカラーとベクトルの外積となり意味をなさないので,ダメということ。
また,公式中に現れる内積は交換法則にしたがって順序を交換しても構いません。たとえば,(1)中右辺の(x ・z )は(z ・x )であってもいいわけです。さらに一般にベクトル,スカラーには,
(X ・Y )Z =Z (X ・Y ) [ スカラーとベクトルの積 ]
X ・(Y ×Z ) = (Y ×Z )・X [ ベクトルとベクトル積との内積 ]
のような交換関係があります。しかし,べクトルと微分作用素(次章を参照)が混ざると上の交換則が成り立たない場合があります。
証明は,パスさせてもらいますが,少しコメントを付け加えておきます。外積:x ×y =z の成分(z1,z2,z3)は行列式,
1 1 1 x1 x2 x3 y1 y2 y3
の一行目の余因子[#],に対応していることを覚えておくと便利です。すなわち,
(z1,z2,z3)=(Δ11,Δ12,Δ13)
| Δ11= | x2 | x3 | ,Δ12=- | x1 | x3 | ,Δ13= | x1 | x2 | ||||||||||||
| y2 | y3 | y1 | y3 | y1 | y2 |
と書けます。これを利用すると,x ×y (=z),x,y から作られる次のスカラー三重積は,
z ・(x ×y )= z1 z2 z3 = z1Δ11+z2Δ12+z3・Δ13 x1 x2 x3 y1 y2 y3
= z12+z22+z32 =|z|2
=|x ×y|2 > 0 ( x と y は1次独立として)
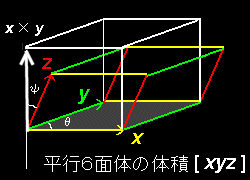 のように計算でき,正の値をとります。3つのベクトル,x ,y ,x×y を順に並べてつくった行列式は常に正と言いかえてもいいでしょう。その理由はスカラー三重積の幾何学的な意味が,右図に示すようにベクトルx ,y のつくる平行四辺形を底面,高さを |x ×y | とする平行六面体の体積だからです。
のように計算でき,正の値をとります。3つのベクトル,x ,y ,x×y を順に並べてつくった行列式は常に正と言いかえてもいいでしょう。その理由はスカラー三重積の幾何学的な意味が,右図に示すようにベクトルx ,y のつくる平行四辺形を底面,高さを |x ×y | とする平行六面体の体積だからです。
より一般的に3つのベクトルX,Y,Z (≠X×Y) のスカラー3重積 Z ・(X ×Y )の絶対値がベクトルX,Y,Z のつくる平行6面体の体積と等しくなっています。つぎのように書くとわかりやすい?
[X Y Z ]={|Z |cosψ}{|X ||Y |sinθ}
ここで,絶対値をとる理由は右図のように,0<ψ<π/2 (右手系)のときのスカラー三重積は正の値をとりますが,角度がπ/2<ψ<π(左手系)にあるときはマイナスの符号を必要とするからです。スカラー三重積が 0 となるとき,ベクトルX,Y,Z は1次従属です。絶対値をとる前のスカラー3重積 Z ・(X ×Y ) を特に 擬スカラーと呼ぶことがあります。これはベクトルZと擬ベクトルX ×Y の内積から作られるスカラーであって,X ,Y ,Z をX → -X ,Y → -Y,Z → -Z のように反転させると,[X Y Z ] → [-X -Y -Z ]=-[X Y Z ]と符号を変えるからです。もともとのスカラー積(内積)X ・Y は座標を反転しても符号を変えない性質をもっているためこのように区別することになります。
[1] 相反基底
1次独立な3つのベクトル,{a1,a2,a3}を基底とするとき,
|
← 物理では, am・bn = 2πδmn と定義することも多い。 | ||
をみたすbn からなる基底,{b1,b2,b3}を相反基底といいます[#]。具体的には,
b1 = a2×a3 ,b2 = a3×a1 ,b3 = a1×a2 [a1a2a3] [a1a2a3] [a1a2a3]
とおけば,相反基底となります。 ここで分母はスカラー3重積[a1a2a3]≠0 です[#]。また,対称性から,
a1 = b2×b3 ,a2 = b3×b1 ,a3 = b1×b2 [b1b2b3] [b1b2b3] [b1b2b3]
と書きなおせます。
[2] 基底{a1,a2,a3}とその相反基底{b1,b2,b3}に関して,
| 公式3 (1)任意のベクトル d について, d = ( d ・b1 ) a1 + ( d ・b2 ) a2 + ( d ・b3 ) a3 ; [a1a2a3] ≠ 0
|
証明
(1) 公式2の(5)より,
[x y z ]v = [x y v ]z -[z v x ]y + [z v y ]x
ここで,x, y,z ,v → a1,a2,a3,d と記号を変え,
[a1a2a3]d = [a1a2d ]a3-[a3da1]a2+ [a3d a2]a1
公式2の(2)'を用いて並び換えれば,
↓ スカラー3重積の定義=公式2の(2)
d = 1 [d a2a3]a1 +[d a3a1]a2 +[d a1a2]a3 [a1a2a3] = ( d ・b1 ) a1 + ( d ・b2 ) a2 + ( d ・b3 ) a3
= 1 d ・(a2×a3)a1 +d ・(a3×a1)a2 +d ・(a1×a2)a3 [a1a2a3]
(2) 公式2の(6)より,
[a1a2a3] = a1・a2×a3 = b2×b3 ・ b3×b1 × b1×b2 [b1b2b3] [b1b2b3] [b1b2b3]
= [b1b2b3]2 = 1 [b1b2b3]3 [b1b2b3]
クロネッカーのδとエディントンのεの性質をまとめておきましょう。 → [#]
δst= 1 s=t 0 s≠t
εijk= ε123=ε231=ε312 = 1 ε321=ε213=ε132 = -1 εその他 = 0
σ(εijk)=-εijk [σ:互換操作 [#]]
εsjkεsmn δjm δjn =δjmδkn-δjnδkm δkm δkn
εstjεstk=2δjk
εstuεstu=6
赤い字では和の規約を用いてます。
[1] 異なる2つの座標系の基底ベクトルを,Σ ={e1,e2,e3},Σ'={e'1,e'2,e'3} とします。ベクトルx はそれぞれの座標系で,
x = xe1+ye2 +zen (座標系Σ)
x =Xe'1+Ye'2+Ze'n (座標系Σ')
とします。Σ'の各基底ベクトルe'jもベクトルの一つですから座標系Σの基底を用いて一次結合で表せます。それを
e'1= p11e1+p21e2+p31e3 ≡(p11,p21,p31)
e'2= p12e1+p22e2+p32e3 ≡(p12,p22,p32)
e'3= p13e1+p23e2+p33e3 ≡(p13,p23,p33)
とします。この pjk はΣ とΣ' が与えられると同時に定まるものです。 このとき,各座標系におけるベクトル成分の関係は行列を用いて表すと,
x p11 p12 p13 X y = p21 p22 p23 Y z p31 p32 p33 Z
となります。詳細は →[#] 。 ここで,
P ≡ p11 p12 p13 p21p22 p23 p31 p32 p33
を 座標変換の行列 (または,基底変換の行列) といいます。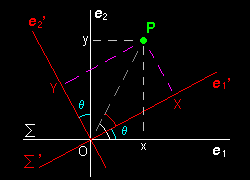
[2] 特別な場合として,3次元空間の z 軸周りで角度θの回転を,
回転前 Σ(x,y,z) → 回転後 Σ'(X,Y,Z)
とすると,z = Z なのでで,x-y平面内の原点周りの回転と考えて,
e'1= p11e1+p21e2 = cosθe1+sinθe2
e'2= p12e1+p22e2 =-sinθe1+cosθe2
および,
x = p11 p12 X = cosθ -sinθ X y p21 p22 Y sinθ cosθ Y
ここで,
P(θ)= cosθ -sinθ sinθ cosθ
は回転行列です。
[3] 時刻とともに連続的に回転する座標系については,コリオリの力をぜひ見ておいてください→[#]