
 |
4 複素ベキ級数関数 | |
| f-denshi.com [目次へ]最終更新日: | ||
| サイト検索 | ||
[1] 複素関数がベキ級数で表せるか否かは実数関数の場合より特に重要な意味があります。実数関数の場合,1階微分可能でもベキ級数で表せない関数はいくらでもあります[#] が,複素関数の場合,微分可能な関数はすべてベキ級で表わすことができます。そしてベキ級数で表せる複素関数は何回でも微分可能です。これは,”複素関数は1階微分できれば,何回でも微分可能である”という結構大変なことを示しています。(これが微分可能な複素関数に対して正則関数という用語を好んで使う理由です。)にもかかわらず,実数のベキ級数を十分理解しているならば,複素ベキ級数に関して,新たに付け加えるべき数学的な内容はあまりありません。
[2] その理由は,複素数z のベキ級数について展開される議論は,実数のときの議論において,|r|⇒|z|と読み換えるだけで,そっくりそのまま使えるのです。それを保証するのが実数ベキ級数の絶対収束[#]に相当する次の定理です。
定理 [複素数のベキ級数の収束性]について,z=z0 で収束するならば,|z|<|z0|をみたすすべての複素数 z についての級数 |c0|+|c1||z|+|c2||z|2+・・・+|cn||z|n+・・・ が絶対収束する。 |
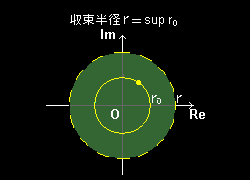 [3] すぐに気づくことですが,この定理は z0 として特に実数,r0+i 0(つまり,ガウス平面の実軸上の点)を考えて,あるベキ級数が収束すれば,ガウス平面の原点を中心とする半径|z0|の円の内部にある複素数すべてについてこのベキ級数が収束することを保証しています。
[3] すぐに気づくことですが,この定理は z0 として特に実数,r0+i 0(つまり,ガウス平面の実軸上の点)を考えて,あるベキ級数が収束すれば,ガウス平面の原点を中心とする半径|z0|の円の内部にある複素数すべてについてこのベキ級数が収束することを保証しています。
したがって,「実数についてのベキ級数に関する議論が複素数における議論でも,
|r| →|z| とするだけでそのまま成り立つことになるのです。
[4] 収束半径,もしくは収束円と呼ばれる概念について複素数の場合についてもまとめておきましょう。
上の定理における|z0|の上限[#],
| r ≡sup|z0| [ 収束半径 ] |
を収束半径といい,原点中心,半径 r の円を収束円といいます。特にすべての複素数について収束する場合,収束半径は無限大 : r =∞ といいます。(ちょうど,|z| = r となる z については,ベキ級数によって収束したりしなかったりで各論となります。)収束半径という言葉は,実数のときと違い(←実数のときは”収束線分”が正しい用語?)文字通り「ガウス平面上の円の半径」となっています。
[5] コーシー・アダマールの定理
収束半径を求めるには次の定理が役立ちます。
| コーシー・アダマールの定理 複素数ベキ級数: c0+c1z+c2z2+・・・+cnzn+・・・の収束半径 r と係数 cn との関係は, または, となる。ただし,1/∞ = 0, 1/0 =∞ とする。 |
例
ez≡1+ 1 z+ 1 z2+ 1 z3+・・・+ 1 zn ・・・ 1! 2! 3! n!
の収束半径は?
1 = |cn+1| = |n!| = 0 r |cn| |(n+1)!|
したがって,
収束半径r は無限大,つまり,どんなzについても収束する。