| 111 グリーン関数入門 | |
| f-denshi.com 更新日: 04/02/25 | |
[1] x に関する線形演算子 L [#] を用いて次のように表すことができる微分方程式,
L[p(x)]=q(x) ← L p(x) = q(x) とも書く
の解を形式的(=無理やり!)に,
p(x)=L-1[q(x)] ← p(x) = L-1q(x) とも書く
と書いたときのLの逆演算子 L-1 を
G ≡ L-1
と書いてグリーン演算子 G と言います。
あるいはもう少し具体的に微分方程式の形式解を,
p(x) = G(x,x')q(x')dx' ・・・・・ [公式 1]
という形式で表したときの G(x,x') をグリーン関数と定義します。この右辺は,フーリエ変換における ”たたみ込み” に相当し,G*q(x) としばしば記述されます[#]。
[2] グリーン関数は微分方程式の演算子を利用した解法に利用されますが,具体的な関数形は線形演算子 L に依存して様々です。また,[公式 1] の両辺に L を作用させると,( Lは変数 x にだけ作用することに注意して )
L[p(x)] =L G(x,x')q(x')dx' = L[G(x,x')]q(x')dx'
ここで,L[p(x)] が q(x) に等しいので,上式は,
q(x) = L[G(x,x')]q(x')dx'
この式は,L[G(x,x')] がデルタ関数 [#],すなわち,
L[G(x,x')] = δ(x−x') ・・・・・ [公式 2 ]または,x−x'=X として, L[G(X)] = δ(X) ・・・・・ [公式 2' ] |
でなければならないことを示しています。これはグリーン関数のもっとも基本的な性質で,グリーン関数を用いて微分方程式を解く時はたいていこの方程式から議論が始まります。
補足: 量子力学のブラ・ケット記法を知っているならば,方程式,
L|α>=|β> の左から L-1 をかけて,( L-1L = I (恒等演算子)に注意して ) |α>=L-1|β>=G|β> と書いたときの G (=L-1) をグリーン演算子,その連続基底 |x> で展開した表現, ↓↑
における <x|G|x'> = G(x,x') をグリーン関数といいます。 ・・・ と理解してもいいでしょう。 |
[3] グリーン関数の例を挙げておきましょう。まず,電磁気学から。
−例1−
ポアッソン方程式 ( L ≡−εΔ ) の場合, [#]
−εΔΨ(r ) = ρ(r ) ⇔ −εΔ[Ψ]=ρ(r )
を考えて見ましょう。 この解はよく知られているように [#],
Ψ(r )= ρ(r ') dr '
4πε|r −r '|
これを,グリーン関数の定義式[公式 1]の3次元版,
p(r ) = G(r,r ')q(r')dr '
と比べると,L ≡−εΔ をはじめとして,
p(r ) → Ψ(r )
G(r −r ') → 1 4πε|r −r '|
q(r ) → ρ(r )
と対応していることがわかります。ここでのグリーン関数 G(r −r ') は単位点電荷のポテンシャルであって,
L[G(r −r ')] =−εΔG(r −r ') = δ(r −r ' )
が成り立っている[#] ことに注意してください。もちろんこれは[公式2]に相当します。
 [4] −例2−
[4] −例2−
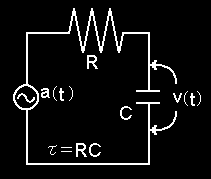
入力電圧 a(t) に対して右図の RC回路のキャパシタ両端に出力される電圧 v(t) を求める微分方程式は,RC=τとおいて,
L[v(t)] = τ dv(t) +1 v(t) = a(t) ・・・・・ (1) dt
となります[#]。そのグリーン関数 G(t,t')を用いた形式解を,
v(t) = G(t,t')a(t')dt' ≡ G*a(t ) ・・・・・ [*]
とすれば,[公式2]より,
L[G(t,t')]=τ dG(t−t') + G(t−t') = δ(t−t') ・・・・・ [**] dt
が成り立ちます。ここで,[*] は G(t) と a(t)との「たたみ込み,G*a(t ) です。
この分野の慣習に従って,係数 1 のない ”フーリエ変換”の定義 I [#] を用います。
2π
すると,たたみ込みの定理[#]のより,G(t) と a(t) のフーリエ変換をそれぞれ,H(ω),A(ω) とすれば,
v(t) = G*a (t) = F -1{H(ω)A(ω)}= 1 H(ω)A(ω)ei ωt dω 2π
ただし,
H(ω)=F {G(t)}= G(t)e−i ωt dt
A(ω)=F {a(t)}= a(t)e−i ωt dt
と,H(ω)A(ω) の逆フーリエ逆変換 F -1 を用いて微分方程式の形式解 が示されます。ここで,A(ω)はすぐに計算できるので,結局,H(ω)を求めることに問題は帰着されるのです。
[5] そこで, [**] において変数を,t−t' →t と変えて両辺,フーリエ変換すれば, ( δ関数については → [#] )
τ dG(t) + G(t) e−i ωt dt = δ(t)・e−i ωt dt ・・・・・ (2) dt
この右辺は,δ関数の性質から
δ(t)・e−i ωt dt = e−i ω・0 = 1
左辺については, G(±∞)= 0 という境界条件で,
dG(t) e−i ωt dt dt
= G(t)・e−i ωt ∞ − G(t)・(-iω)・e−i ωt dt = iω G(t)・e−i ωt dt -∞
であることに注意すれば,(2)は,
(τiω+ 1)G(t)e−i ωt dt = 1
すなわち,G(t)のフーリエ変換 H(ω) は,
G(t)e−i ωt dt = 1 ⇒ H(ω) τiω+ 1
で得られます。 なお,この H(ω) はしばしば,周波数応答関数と呼ばれます。
G(t) はこの逆フーリエ逆変換である,
G(t) = 1 H(ω)ei ωt dω= 1 ei ωt dω 2π 2π iωτ+1
を積分することで求まります。
コンデンサーの両端に現れる電荷を±Qとすれば,
Q=Cv,
| I = | dQ | =C | dv |
| dt | dt |
| ∴ a(t) = RI+v(t) = RC | dv | + v(t) これが(1)式 | |
| dt | |||
F [ h*g(t)] = F [h(t)]・F [g(t)]
逆に,f,g が区分的に連続で,(f*g)が点 t で連続なら,
h*g (t) = F -1{F [ h(t) ]F [ g(t) ] }