ときわ台学/微分方程式/ルジャンドル陪微分方程式･ルジャンドル陪多項式

	432 ルジャンドル陪関数
f-denshi.com 更新日：

１．ルジャンドルの陪微分方程式

ルジャンドルの陪微分方程式　　　

(1－x²)y''－2ｘy'＋ ν(ν＋1)－ m² y ＝ 0

1－x²

　ν ＝ 0，1，2，・・・・・

の一般解はルジャンドル陪関数　(ルジャンドル陪多項式)，

ｙ＝

P_ν^m(x) ＝ (1－x²)^m^/2 ・ d^m P_ν(x)

dx^m

m ＞ 0 のとき

　　　　　＝ (1－x²)^m/2 d^ν＋m (x²－1)^ν

2^ν ν！ dx^ν＋m

P_ν⁰(x) ＝ P_ν(x) m ＝ 0 のとき

P_ν^m(x)＝(－1)^|m| ・ (ν－|m|)！ P_ν^|m|(x)

(ν＋|m|)！

m ＜ 0 のとき

　　　　＝ (1－x²)^－|m|/2 d^ν－|m| (x²－1)^ν

2^ν ν！ dx^ν－|m|

で与えられる。P_ν(x)はルジャンドル多項式で，

P_ν(x) ＝ 1 ・ d^ν (x²－1)^ν　　　　　

2^ν ・ν！ dx^ν

m　＝　-ν，-ν＋1，・・・・・， ν－1，ν　

具体的な関数

P₁¹(x)＝(1－x²)^1/2

P₂¹(x)＝3x(1－x²)^1/2

P₂²(x)＝3(1－x²)

P₃¹(x)＝	3(5x²－1)(1－x²)^1/2

	2

P₃²(x)＝15x(1－x²)　

P₃³(x)＝15(1－x²)^3/2

P_ν^m(x)＝＝

(1－x²)^m/2

_(ν-m)/2

^k=0

(-1)^k(2ν－2k)!

x^ν-2k-m

　　　　　　･･･　[*]　

2^ν

k!(ν－k)!(ν－2k－m)!

(ν－m)/2　≡ (ν－m)/2　　　(ν－m：偶数）
　　　　　　　 (ν－m－1)/2　(ν－m：奇数）

［１］　ほとんどの人とにとって，m が非負整数の場合（だけ）が重要なので，以下　m≧ 0 の整数として説明します。

まず，この微分方程式は，m＝0 のときにルジャンドルの微分方程式[#]に帰着されます。もちろん，その時の解はルジャンドル関数です。

m＞0のときは，

P_ν^m(x) ＝ (1－x²)^m^/2 ・ d^m P_ν(x)

dx^m

　　　　＝ 1 (1－x²)^m^/2 d^ν^＋^m (x²－1)^ν　［ロドリゲスの公式］

2^ν ・ν！ dx^ν^＋^m

つまり，

「 P_ν^m(x)　は x に関する 2ν次の多項式を (ν＋m) 回微分している。」　

ので，m＞ν となる m については，P_ν^m(x)≡ 0 となり，意味をもちません。　よって，｜m｜≦ν という条件が付加されています。

　　　P_ν^m(x)が解であることの確認計算

・・・

母関数の話

(2m)！(1－x²)^m/2　 t^m ＝ ∞
Σ
ν=m P_ν^m(x)・t^ν

2^m ・m！ (1－2tx＋t²)^m＋1/2

展開可能性の話

f(x) ＝ a_mP_m^m(x) ＋ a_m+1P_m+1^m(x) ＋ a_m+2P_k^m(x) ＋・・・・・

a_k＝

(k－m)！

(k－m)！

2k＋ 1

2

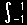f(x)P_k^m(x)dx

公式　　漸化式

(1)　(ν＋1－m) P_ν+1^m ＝ (2ν＋1)x P_ν^m － (ν＋m) P_ν-1^m

(2)　P_ν^m+1 ＝ { 2mx/(1－x²)^1/2} P_ν^m ＋{ m(m－1)－ν (ν＋1) } P_ν^m-1

２．　ルジャンドル陪関数の積分

規格化の話

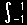P_ν^m(x)・P_ν'^m'(x)dx ＝

(ν＋m)！

(ν－m)！

2

2ν＋ 1

・δ_νν'δ_mm'

［目次へ］

P₁¹(cosθ)＝sinθ	P₂²(cosθ)＝(3/2)(1－cos2θ)
	P₂²(cosθ)＝(3/2)(1－cos2θ)

＝	1	(1－x²)^m^/2	d^ν^＋^m	(x²－1)^ν　［ロドリゲスの公式］

	2^ν ・ν！		dx^ν^＋^m

(2m)！(1－x²)^m/2	t^m	＝	∞ Σ ν=m	P_ν^m(x)・t^ν

2^m ・m！	(1－2tx＋t²)^m＋1/2

２． ルジャンドル陪関数の積分

２．　ルジャンドル陪関数の積分