434　球面調和関数
f-denshi.com  更新日：

１．

［１］　球座標で表したラプラシアン [#] の角度部分である微分演算子：

Λ ≡

1

･

∂

sinθ

∂

＋

1

･

∂2

(　≡⊿θ,ψ )　････　[*]

sinθ

∂θ

∂θ

sin2θ

∂φ2

を含む次のような微分方程式，

球座標におけるラプラス方程式 ΛY(θ，φ)＋ν (ν ＋1)Y(θ，φ) ＝ 0    ；　ν ＝ 0，1，2，　　････　[**]

の解を球面調和関数といいます。

［２］　この微分方程式は，

Y(θ，φ)＝ P(θ)Φ(φ)

とおいて[**]  に代入すれば，

sinθ	･	∂		sinθ	∂P(θ)		＋ ν(ν＋1)sin2θ ＝ －	1	･	∂2Φ(φ)
P(θ)		∂θ			∂θ			Φ(φ)		∂φ2

と，左辺はθだけ，右辺はφだけの関数に変数分離され，両辺がいつも等しい値をとるためには，両辺がある定数に等しくなければなりません。  そこでその値を m² とおくとラプラス方程式[**]は，

∂2Φ(φ)	＝ －m2 Φ(φ)　　　　　　　　　　　　　　　　　　　　･･････　　(１)
∂φ2

sinθ	･	∂		sinθ	∂P(θ)		＋ ν(ν＋1)sin2θ ＝ m2 　･･･　(２)
P(θ)		∂θ			∂θ

という２つの方程式を解くことに帰着されます。　(１)はすぐに解けて，

Φ(φ) ＝ φ_m(φ) ≡ c･exp(i mφ)，

一方，(２) は，変数を，x＝cosθ，　sinθ＝(1－x²)^1/2　と変数変換すれば [#]，

(1－x2)P''(x)－2ｘP'(x)＋		ν(ν＋1)－	m2		P(x) ＝ 0
			1－x2

と書き直されます。これはルジャンドルの陪微分方程式[#] です。　つまり，P(x)はルジャンドルの陪関数で与えられます。

［３］　したがって，記号を改めて，

Y(θ，φ) ≡ Yνm(θ，φ) ≡ CνmPνm(cosθ)･φm(φ)

ここで，

ν ＝  0，1，2，･･･　  
m　＝　-ν，-ν＋1，･･･，0，･･･，ν－1，ν　　　

であり，任意定数 C_νm は球面調和関数に規格化条件を課すことで定めます。 すなわち，

	｜Yνm(θ，φ)｜2 dΩ ＝	｜Cνm｜2		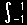	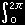｜Pνm(x)｜2｜exp(i mφ)｜2 dφdx ＝ 1

という条件を加えれば，

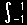Pνm(x)･Pν'm'(x)dx ＝

(ν＋m)！ (ν－m)！

2 2ν ＋ 1

･δνν'δmm'

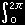	φ*m (φ)･φm' (φ)dφ 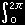＝		exp(－i mφ)･exp(i m'φ)dφ ＝ 2πδmm'

であることに注意して [#]，

Cνm　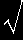＝		2ν ＋ 1 ･ (ν－m)！ 4π (ν＋m)！

となります。

［４］　まとめると，

ラプラス方程式，      ΛY(θ，φ)＋ν (ν ＋1)Y(θ，φ) ＝ 0         ；　ν ＝ 0，1，2，　････  の解は，球面調和関数，  　    Yνm(θ，φ) ＝ 2ν ＋ 1 ･ (ν－m)！ 4π (ν＋m)！ 　Pνm(cosθ)･exp(i mφ) である。

 ［５］　この微分方程式の意味　⇒　軌道角運動量

L² ＝ －h²Λ　　　　⇒　　　　L²Y(θ，φ) ＝ ν (ν ＋1)h²Y(θ，φ)　

最後に球面調和関数の具体的な形を見ておくことも重要でしょう。

球面調和関数
Yνm		θ-φ座標	デカルト座標	｜Yνm｜
ν ＝0	m＝0	1 4π	1 4π
ν ＝1	m＝0	3 4π  cosθ	3 4π z r
	m＝±1	3 4π･2  sinθｅ±iφ	3 4π･2 x±i y r
ν ＝2	m＝0	5 4π･4 (3cos2θ－1)	5 4π･4 3z2－r2 r2
	m＝±1	5･3 4π･2 (sinθcosθ)ｅ±iφ	5･3 4π･2 z(x±i y) r2
	m＝±2	5･3 4π･8 sin2θ･ｅ±2iφ	5･3 4π･8 (x±i y)2 r2
ν ＝3	m＝0	7 4π･4 (5cos2θ－3cosθ)	7 4π･4 z(5z2－3r2) r3
	m＝±1	7･3 4π･16 (5cos2θ－1)sinθ･ｅ±iφ	7･3 4π･16 (x±i y)(5z2－3r2) r3
	m＝±2	7･15 4π･8 cosθsin2θ･ｅ±2iφ	7･15 4π･8 z(x±i y)2 r3
	m＝±3	7･5 4π･16 sin3θ･ｅ±3iφ	7･5 4π･16 (x±i y)3 r3

*  デカルト座標表示は，r ＝ 1 として，表記することもあります。

以上，球面調和関数を複素関数としてそのまま使いましたが，実用上は基底をとり直した立方調和関数 [#] がよく使われますのでそちらも参考にしてください。

デカルト座標を球面調和関数で表すと，

x ＝	2π 3	r {Y1-1(θ，φ)＋Y11(θ，φ)}

y ＝ i	2π 3	r {Y1-1(θ，φ)－Y11(θ，φ)}

z ＝	4π 3	r Y10(θ，φ)

［補足1］

変数を，x＝cosθ，　sinθ＝(1－x²)^1/2　と変換すれば[#]，

dx ＝ －sinθ･dθ ＝ －(1－x²)^1/2 dθ

d	＝－(1－x2)1/2	d
dθ		dx

d2	＝  －	d(1－x2)1/2	･	d		－(1－x2)1/2･	d		d
dθ2		dθ		dx			dθ		dx

＝  －	d(1－x2)1/2	･	dx	･	d	＋(1－x2)･	d2
	dx		dθ		dx		dx2

＝  －x ･	d	＋ (1－x2)･	d2
	dx		dx2

［目次へ］

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002

以下メモが書き

球面調和関数との関係

Yνm(θ，φ)？＝	(－1)(m+|m|)/2		(2ν+1)(ν -|m|)！		1/2	exp(imφ)･Pν |m|(cosθ)
			4π(ν+|m|)！

∇² V ＝ 0　の解は

V(x，y，z)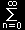＝			αnrn＋	βn		×		Pn(cosθ)＋	Σ	(amcosmφ＋bmsinmφ)Pmn(cosθ)
				rn+1