 |
A1 振動現象 |
|
| f-denshi.com 更新日: 執筆中 |
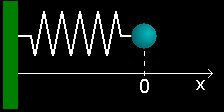
簡単な微分方程式の例としてバネにつながれたおもりの振動を考えてみましょう。
1.単振動
[1]バネにつながれたおもり(=質点, 質量 m )に対するニュートンの運動方程式はよく知られているように,
| m |
d2x |
=−bx = F [復元力] ( =−mω02x ) ・・・・・ [*] |
|
| dt2 |
で与えられます[フックの法則]。ここで,x はバネのつりあいの位置からの質点の変位,b はバネ定数と呼ばれ,変位 x が小さいときは復元力 F が -bx で近似できることをこの方程式は示しています。
この2階微分方程式[#] の解が正弦波, または余弦波で得られることは,
| x = A sin(ωt+φ) : ただし, ω= |
|
( b = mω2 ), A,φ=適当な定数 |
を[*]に代入してみればすぐに確かめられます。ここで,A は定数で,振幅と呼ばれます。また,ωは角振動数と呼ばれ,振動数νと,
 ω= 2πν
ω= 2πν
と関係付けられます。
[2] また,複素数解を認めれば,
x = A exp (iωt)
も解となります。これも [*] に代入して計算して確かめてください。
2.減衰する波
[1] 再び,バネにつけられた質点の振動を考えます。ただし,今度はバネは質点の速度と質量に比例する(比例定数=2γ) ような摩擦抵抗を受けて,振動が時間とともに衰えていくような場合を考えます。その場合の運動方程式は,
b = mω02
とおいて,次のようになります。
| m |
d2x |
= |
−bx |
−2γm |
dx |
( = F ) |
⇔ |
d2x |
+2γ |
dx |
+ω02x = 0 ・・・・・ [**] |
|
|
|
|
| dt2 |
dt |
dt2 |
dt |
|
復元力 |
+ 摩擦抵抗 |
= 働く力 |
|
|
|
|
|
|
|
|
|
| この解は,ω'= |
 |
ω02−γ2 |
|
,ω''= |
 |
γ2−ω02 |
を定義して用いれば, |
(1)減衰振動
小さな摩擦,γ<ω0
ω'>0 |
A e-γt sin(ω't+φ) |
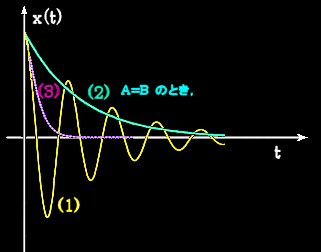 |
(2)臨界減衰
ω02=γ2 |
(A+Bt) e-γt |
(3)過減衰
大きな摩擦,γ>ω0
ω''>0 |
A exp[−(γ+ω'')t]
+B exp[−(γ−ω'')t] |
となります。(これは摩擦を受けながら振動するおもりが静止する様子をあらわす他に,光が物質中で吸収されれて減衰していく様子にも応用されます。)
導出方法
x(t)=e-γt・y(t)とおいて,[**]に代入すると, ←波動方程式を解くときの定番テクニック
| d2y(t) |
e-γt−2γ |
dy(t) |
e-γt+γ2e-γt・y(t)+2γ |
dy(t) |
e-γt+2γ(−γ)e-γt・y(t)+ω02y(t)e-γt=0 |
|
|
|
| dt2 |
dt |
dt |
 |
d2y(t) |
+(ω02−γ2)y(t) |
 |
e-γt= 0 [**]' |
|
| dt2 |
[2] ここで,摩擦が小さく,ω02−γ2≡ωs2 >0 場合,
これは最初に扱った問題の,[*]で,ω→ωs とした微分方程式にすぎないので,その解は,
y(t) = A sin(ωst+φ) ; A,φ=定数
したがって,
x(t)=Ae-γt・sin(ωst+φ)
これは振幅が指数関数的に減衰する振動をあらわしています。
[3] 次に,ω02−γ2=0 の場合,[**]'は,
に等しく,その一般解は,
y(t) = A+Bt
したがって,初めの微分方程式の解は,
x(t)=(A+Bt)e-γt
=B(t+A/B)e-γt
[4] 摩擦が大きく,ω02−γ2=−ωL2 < 0 場合,
この解は,
y(t)=exp[ωLt] または,exp[−ωLt]
したがって,
x(t)=A exp[-(γ+ωL)t]+B exp[-(γ−ωL)t]
ここで, γ−ωL>0 であることに注意すれば,この解は2つの指数関数的な減衰の重ね合わせであることがわかります。
[3] 複素数解
3.強制振動
[1] 次に,中心力に束縛された物体に摩擦抵抗と周期的な強制力が働く場合を考えましょう。[**]に強制力 F/m=fcosωt を追加します。
| d2x |
=−2γ |
dx |
−ω02x + f ・cosωt [強制振動] ・・・・・ [***] |
|
|
| dt2 |
dt |
この微分方程式の解を, x=Acos(ωt−φ) とおいて代入すると,
−Aω2cos (ωt−φ) = 2γAωsin (ωt−φ)−ω02Acos (ωt−φ) + f ・cosωt
加法定理[#] を使って整理すると,
[ −ω2Acosφ+2γAωsinφ+Aω02cosφ−f ]cosωt
+A[ −ω2sinφ−2γωcosφ+ω02sinφ ]sinωt=0
すなわち,
(1) −ω2Acosφ+2γAωsinφ+Aω02cosφ−f =0
| ⇔ A = |
f |
|
| {(ω02−ω2)+2γω・tanφ}cosφ |
(2) −ω2sinφ−2γωcosφ+ω02sinφ=0
が成り立たたなければなりません。 (2)式から,
| cos2φ = |
1 |
= |
(ω02−ω2)2 |
|
|
| 1+tan2φ |
(ω02−ω2)2+(2γω)2 |
これを用いると,(1)式から,
| A = |
f |
|
|
|
 |
(ω02−ω2)2+(2γω)2 |
|
と求まります。
| x = |
f |
・cos(ωt−φ) [答え] |
|
|
|
 |
(ω02−ω2)2+(2γω)2 |
|
角振動数ω0が
|
|
|
|
| ω0> |
γ |
 |
2 |
であるならば,
|
|
|
| ω = |
 |
ω02−2γ2 |
の時に振幅は最大をとります。
[2] 強制振動が複素関数 f ・exp[iωt] で与えられるときは,
| d2x |
=−2γ |
dx |
−ω02x + f ・exp[iωt] ・・・・・ [***]' |
|
|
| dt2 |
dt |
複素数解を
x(t)=A' exp[iωt]
とおいて,[***]'に代入して,exp[iωt]で割ると,
| A' = |
f |
=f・ |
(ω02−ω2)−2γωi |
|
|
| (ω02−ω2)+2γωi |
(ω02−ω2)2+(2γω)2 |
がすぐに得られます。
4.連成振動と基準モード
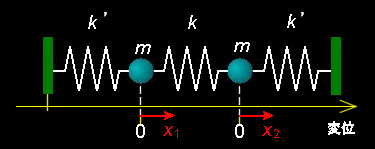 [1] 右図のように壁の間でバネにつながれた質量 m の重りが直線上をフックの法則
[#] にしたがって弾性振動する様子(連成振動)を考えます。ここで,2つの重りどおしは弾性係数k で,また,それぞれのおもりと壁とは弾性係数k'で直線的につながっているものとします。また,2つの重りがともに静止してつりあう位置を基準にしたそれぞれの重りの時刻
t における変位(基準から右側を+,左側を−にとって)を x1(t),x2(t) とします。これらの記号のもとで2つの物体にたいする運動方程式は,
[1] 右図のように壁の間でバネにつながれた質量 m の重りが直線上をフックの法則
[#] にしたがって弾性振動する様子(連成振動)を考えます。ここで,2つの重りどおしは弾性係数k で,また,それぞれのおもりと壁とは弾性係数k'で直線的につながっているものとします。また,2つの重りがともに静止してつりあう位置を基準にしたそれぞれの重りの時刻
t における変位(基準から右側を+,左側を−にとって)を x1(t),x2(t) とします。これらの記号のもとで2つの物体にたいする運動方程式は,
| m |
d2x1 |
= −k'x1 +k(x2-x1) = −(k'+k )x1+kx2 |
・・・・(1) |
|
| dt2 |
| m |
d2x2 |
= −k(x2-x1)−k'x2 = kx1−(k'+k )x2 |
・・・・(2) |
|
| dt2 |
となります。したがって,この「連立微分方程式」を適当な境界条件のもとで解けば,2つの物体の運動を完全に記述することができるはずです。
[2] 一見,複雑そうな連立微分方程式ですが,方程式の対称性に注意して,(1)+(2),および,(2)−(1)をとると,
| m |
d2 |
(x1+x2)= −k'(x1+x2)
・・・・(3) |
|
| dt2 |
| m |
d2 |
(x2−x1)= −(k'+2k)(x2−x1)
・・・・(4) |
|
| dt2 |
が得られます。これらは変数を q1=(x1+x2),q2=(x2−x1)と置き換えれば,新しい変数,q1,q2 に関する独立した2つの微分方程式であり,その解は良く知られた単振動をあらわす関数
[#] で,
q1(t) = c1sin(ω1t +φ1)
・・・・(5)
q2(t) = c2sin(ω2t +φ2)
・・・・(6)
となります。これら2つの単振動 q1(t),q2(t) を連成振動の基準振動といい,c1,φ1,c2,φ2 は境界条件が与えられていれば定まる定数です。 したがって,x1=(q2−q1)/2, x2=(q1+q2)/2 より,
x1(t) = c'1 sin(ω1t +φ1)− c'2 sin(ω2t +φ2)
x2(t) = c'1 sin(ω1t +φ1)+ c'2 sin(ω2t +φ2) |
 ただし,2c1=c'1 ,2c2 =c'2 とおき直しています。これが連成振動の一般解です。
ただし,2c1=c'1 ,2c2 =c'2 とおき直しています。これが連成振動の一般解です。
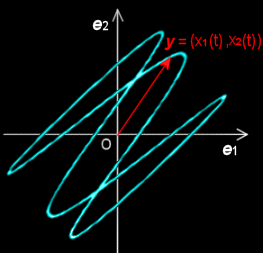
[3] このように簡単に解が得られたポイントは,途中で変数を, x1,x2 から q1,q2 に変換することで,複雑な連立方程式が簡単な2つの独立した単振動をあらわす微分方程式に帰着されたところにあります。この様子を視覚的に見るために変位,x1(t),x2(t) を平面上にプロットして考察してみましょう。つまり,直交基底{ e1,e2 } を用いて,
x = x1(t)e1+x2(t)e2
として平面に解を表すことにするのです(右図がその一例)。すると,先ほど微分方程式を解くためにおこなった座標変換は,ベクトルと行列を用いて,
| = |
|
|
 |
2 |
|
 |
cos(-π/4) |
-sin(-π/4) |
 |
 |
x1 |
 |
| sin(-π/4) |
cos(-π/4) |
x2 |
と書くことができ,これはベクトル成分を平面上で−π/4回転させて,√2 倍することになります。これは成分で考える場合とは逆にπ/4だけ基底ベクトルを回転させて,1/√2
倍するような基底変換をおこなったとみなすこともできます。このまま話を進めても構わないのですが,(3),(4)の両辺√2
で割った座標変換として,
| q1 = |
x1+x2 |
, q2 = |
-x1+x2 |
|
|
|
|
 |
2 |
|
|
|
 |
2 |
|
を考える方がエレガントです。ベクトルで表すと,
 |
q1 |
 |
= |
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
1 |
 |
 |
x1 |
 |
| q2 |
-1 |
1 |
x2 |
| = |
 |
cos(-π/4) |
-sin(-π/4) |
 |
 |
x1 |
 |
| sin(-π/4) |
cos(-π/4) |
x2 |
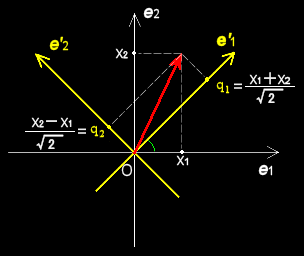 これは−π/4だけの回転を表しています。この様子は右図をよく参考にしてください。この座標変換はユニタリ変換[#] と呼ばれるものです。
これは−π/4だけの回転を表しています。この様子は右図をよく参考にしてください。この座標変換はユニタリ変換[#] と呼ばれるものです。
[3] これは基底変換の立場からみることもでき,形式的に,
 |
e'1 |
 |
= |
 |
cos(-π/4) |
-sin(-π/4) |
 |
 |
e1 |
 |
| e'2 |
sin(-π/4) |
cos(-π/4) |
e2 |
とかかれる基底変換,
Σ;{e1,e2 } ⇒ Σ';{ e'1,e'2 }
をおこなっていることになります。一方,連立方程式(1)〜(4)をベクトルを用いてまとめれば,
| m |
d2 |
x = |
 |
−(k'+k ) |
k |
 |
| k |
−(k'+k ) |
|
x |
・・・・(1)',(2)' |
|
| dt2 |
↓↑ 変数変換
| m |
d2 |
q = |
 |
−k' |
0 |
 |
| 0 |
−(k'+2k) |
|
q |
・・・・(3)',(4)' |
|
| dt2 |
となります。ここまでかけば,もうお分かりですね。ここでの変数変換とは,ユニタリ変換による対称行列の対角化 を行っていることに相当し,連成振動の連立微分方程式を解く問題は固有値問題として捉えられるのです。すなわち,
|
固有方程式,
x K= λx
を解いて,固有値,固有ベクトルを求めて,
λ=−k' のとき,固有ベクトル,e'1
λ=−(k'+2k) のとき,固有ベクトル,e'2
|
を得るということをやっていたわけです。
[4] 固有値問題に帰着できた理由は連成振動に対称性があることにあります。固有値論[#] を勉強したときに,「対称行列は直交行列で対角化することができる」という定理
[#] がありましたね。したがって,ここでの問題で,''重り'' の数がいくら増えても対称性が存在する限り,この問題を固有値問題として取り扱いが可能であることが推測できます。行列の対角化について簡単に復習しておくと,
n次正方行列 T を対角行列 D に対角化するための基底変換:Σ ⇒ Σ' が
e'j = Σukjek ( j,k=1,2,・・・,n ) ←両辺にek との内積をとって,ukj=ek・e'j
で与えられるとき,変換行列 U=(ukj) は直交行列であり,
U*x = q ( x = Uq ) [ベクトルの座標変換]
U*TU = D ( T = UDU* ) [行列の座標変換]
を満足する。// (もちろん,U*はUの随伴行列です。)
このとき,基底Σ上の固有方程式,
Tx = λx
は,
Tx = UDU* Uq = UDq
λx = λUq = Uλq
と計算できることに注意すると,確かに基底Σ'上の固有方程式は,
Dq =λq
と対角行列を用いて表されることになります。 |
[5] 最後に,はじめからこの問題を固有値問題として捉えた解法を示しておきます。まず,
| m |
d2x1 |
= −k'x1 +k(x2-x1) = −(k'+k )x1+kx2 |
・・・・(1)'' |
|
| dt2 |
| m |
d2x2 |
= −k(x2-x1)−k'x2 = kx1−(k'+k )x2 |
・・・・(2)'' |
|
| dt2 |
を行列とベクトルを用いてあらわすと,
|
|
 |
x1 |
 |
= |
 |
−(k'+k ) |
k |
 |
 |
x1 |
 |
| x2 |
k |
−(k'+k ) |
x2 |
↓
ここで,基底変換をおこなって,K を対角化した結果を,
とすれば,
| m |
d2 |
q1 = −mω12q1 =λ1q1 および,m |
d2 |
q2 = −mω22q2 =λ2q2 |
|
|
| dt2 |
dt2 |
|
から2つの特解が任意定数を c1,φ1,c2,φ2 として,
| q1 = c1sin(ω1t +φ1) : ただし,ω1 = |
|
| q2 = c2sin(ω2t +φ2) : ただし,ω2 = |
|
|
|
|
と求まります。 (λ1 , λ2は後で求めます。)
[6] そして,K を対角化する問題は,
 |
−(k'+k ) |
k |
 |
 |
x1 |
 |
=λ |
 |
x1 |
 |
| k |
−(k'+k ) |
x2 |
x2 |
という固有値問題を解くことと同じです。 この固有方程式が自明な x1=x2=0 以外の解をもつ条件は,
|
−λ−(k'+k ) |
k |
|
= 0 |
| k |
−λ−(k'+k ) |
{−λ−(k'+k )}2−k2 = 0
というλの方程式となります。この解は,
λ1 =− k' のとき,固有方程式は,
これより,x1 = x2 ,したがって固有ベクトルは,
| ∴ e'1 = |
|
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
 |
= |
| e1+e2 |
|
|
|
 |
2 |
|
|
| 1 |
λ2 =−( k'+2k ) のとき,固有方程式は,
これより,
x1 = −x2
| ∴ e'2 = |
|
| 1 |
|
|
|
 |
2 |
|
|
 |
-1 |
 |
= |
| −e1+e2 |
|
|
|
 |
2 |
|
|
| 1 |
まとめると,形式的に,
 |
e'1 |
 |
= |
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
1 |
 |
 |
e1 |
 |
| e'2 |
-1 |
1 |
e2 |
したがって,対角化のための基底変換の行列は,
| U*= |
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
1 |
 |
= |
 |
cos(-π/4) |
-sin(-π/4) |
 |
| -1 |
1 |
sin(-π/4) |
cos(-π/4) |
および, ( Uij=ei・e'j 内積 ,e())
| U= |
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
-1 |
 |
= |
 |
cos(π/4) |
-sin(π/4) |
 |
| 1 |
1 |
sin(π/4) |
cos(π/4) |
したがって,x = Uq を成分で計算すれば,
 |
x1 |
 |
= |
| 1 |
|
|
|
 |
2 |
|
|
 |
1 |
-1 |
 |
 |
q1 |
 |
= |
| 1 |
|
|
|
 |
2 |
|
|
 |
q1−q2 |
 |
| x2 |
1 |
1 |
q2 |
q1+q2 |
よって,
x1(t) = c'1 sin(ω1t +φ1)− c'2 sin(ω2t +φ2)
x2(t) = c'1 sin(ω1t +φ1)+ c'2 sin(ω2t +φ2) |
と一般解が求められました。ここで,c'1 ,φ1,c'2 ,φ2 は任意定数。
[7] ついでに確かめておくと,
| U*KU = |
|
 |
1 |
1 |
 |
 |
−(k'+k ) |
k |
 |
 |
1 |
-1 |
 |
| -1 |
1 |
k |
−(k'+k ) |
1 |
1 |
= ・・・計算 ・・・
| = |
 |
-k' |
0 |
 |
| 0 |
-(k'+2k) |
[目次へ]
ω= 2πν

 [1] 右図のように壁の間でバネにつながれた質量 m の重りが直線上をフックの法則
[#] にしたがって弾性振動する様子(連成振動)を考えます。ここで,2つの重りどおしは弾性係数k で,また,それぞれのおもりと壁とは弾性係数k'で直線的につながっているものとします。また,2つの重りがともに静止してつりあう位置を基準にしたそれぞれの重りの時刻
t における変位(基準から右側を+,左側を−にとって)を x1(t),x2(t) とします。これらの記号のもとで2つの物体にたいする運動方程式は,
[1] 右図のように壁の間でバネにつながれた質量 m の重りが直線上をフックの法則
[#] にしたがって弾性振動する様子(連成振動)を考えます。ここで,2つの重りどおしは弾性係数k で,また,それぞれのおもりと壁とは弾性係数k'で直線的につながっているものとします。また,2つの重りがともに静止してつりあう位置を基準にしたそれぞれの重りの時刻
t における変位(基準から右側を+,左側を−にとって)を x1(t),x2(t) とします。これらの記号のもとで2つの物体にたいする運動方程式は, ただし,2c1=c'1 ,2c2 =c'2 とおき直しています。これが連成振動の一般解です。
ただし,2c1=c'1 ,2c2 =c'2 とおき直しています。これが連成振動の一般解です。 これは−π/4だけの回転を表しています。この様子は右図をよく参考にしてください。この座標変換はユニタリ変換[#] と呼ばれるものです。
これは−π/4だけの回転を表しています。この様子は右図をよく参考にしてください。この座標変換はユニタリ変換[#] と呼ばれるものです。