| 11 ガンマ分布 | |
| f-denshi.com 最終更新日:13/10/05 | |
| サイト検索 | |
[1] 平均3個/年でガラスのコップを割ってしまうジロー君,コップ1ダース1セットを箱買いした。はたして,ジロー君が1箱すべてのコップを割ってしまうまでにかかる時間(年)はどのような分布になるであろうか。ただし,同時に2個以上のコップを使うことはせず,一つのコップが割れるごとに新しいコップを箱から取り出してきて使うこととする。
その答えは,次のような確率密度関数で表される「ガンマ分布」となる。
|
||||||||||||
ここで,β=1/λで,場合によってβとλを使い分ける。また,とりあえず,α=正整数と考えておく。
[2] この問題は,ひとつのコップが割れるまでにかかる時間が指数分布に従うことを思い出せば[#],
問題:「同じ指数分布に独立に従う確率変数,X1,X2,・・・,Xα の和,X1+X2+・・・+Xαの従う確率分布を求めよ」
という問題に一般化できる。
証明は,まず,ひとつのコップが従うべき指数分布を,
f1(x)=f2(x)=・・・=fα(x)=λe-λx (=e(λ) 指数分布)
とおく。次に最も簡単なα=2の場合である,X1+X2の従う確率分布Γ(2,λ)は,f1(x)とf2(x)とのたたみ込み[#]を計算すれば得られるが,その際,f1(x)f2(x)>0であるためには積分範囲が,x-x2,x2>0,すなわち,0<x2<xでなければならないことに注意する必要がある。すなわち,
| f1(x-x2)f2(x2)dx2= | λe-λ(x-x2)・λe-λx2 dx2 | ||||||
=λ2xe-λx
これは[*]において,α=2,としたガンマ分布Γ(2,λ)である。
[3] さらに,α-1のとき,[*]が成立する仮定して,Γ(α-1,λ)とΓ(1,λ)=λe-λxとのたたみ込みを計算すると,
λα-1 (x-y)α-2e-λ(x-y) ・λe-λydy Γ(α-1)
= λαe-λx (x-y)α-2 dy Γ(α-1)
= λα ・ 1 xα-1e-λx ↓ Γ(α-1)(α-1)=Γ(α) Γ(α-1) α-1 =Γ(α,λ)
= λα xα-1e-λx Γ(α)
となる。つまり,数学的帰納法を使えば,任意の正整数αについて,問題の解答が[*]で与えられることが示された。ジロー君が1箱(12個)を空にするまでにかかる時間の分布はΓ(α,λ)=Γ(12,3)ということになる。以下,ジロー君のコップの指数分布(1個)とガンマ分布(1箱)の比較を示す。
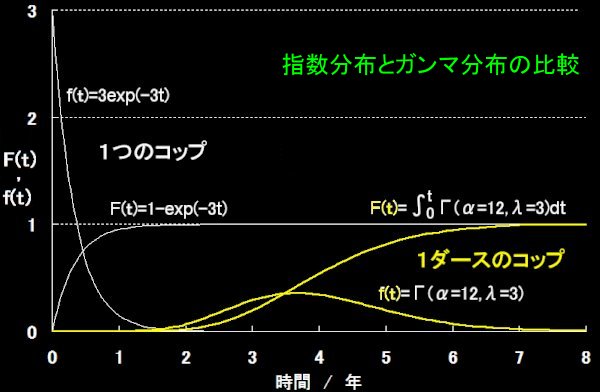
[4] Γ分布の定義についてきちんと書いておく。
|
ガンマ分布Γ(α,β)
ただし,
また,λ=1/βとして定義を与えることもある。 |
ここで,Γ(s)のsはここまで正整数として考えてきたが,半整数もアリということに拡張する。
[5] すると,α→n/2,β→2とした分布関数は,
f(x)= 1 xn/2-1e-x/2 2n/2Γ(n/2)
となり,Γ(α,β)=Γ(n/2,2)の場合が自由度nのカイ二乗分布χ2(n)[#]となっている!ことがわかる。
ここでもう一度,指数分布はガンマ関数において,Γ(α,β)→Γ(1,1/λ)=e(λ)=λexp(-λx) とすることで得られることを思い出そう。ガンマ関数はいろいろな分布を取り出せる打ち出の小槌なのだ。
[6] ガンマ分布の積率母関数,期待値,分散は,
MX(t)≡E(etX) =(1-βt)-α
E(X)=αβ
V(X)=αβ2
証明は各自の演習に任せる。
また,2つのガンマ分布Γ(α1,λ),Γ(α2,λ)に従う確率変数の和がΓ分布(α1+α2,λ)に従うことは,ガンマ分布が指数分布に従う確率変数の和が従う分布として定義されていることからほぼ自明である(=パラメータαに関しての分布の再生性)。つまり,Γ分布(α1+α2,λ)は独立に指数分布 e(λ)に従う確率変数の和,X1+・・・+Xα1+α2 の従う分布なので。
とりあえず,ここまで。