６　線積分
f-denshi.com   ［目次へ］　最終更新日：
サイト検索

１．　ベクトル関数の線積分

［１］　ベクトル A ＝(A₁，A₂，A₃) が領域 D で定義されたC¹級関数[#]：

A₁＝A₁(x，y，z)， A₂＝A₂(x，y，z)， A₃＝A₃(x，y，z)

を用いて定義されているとします。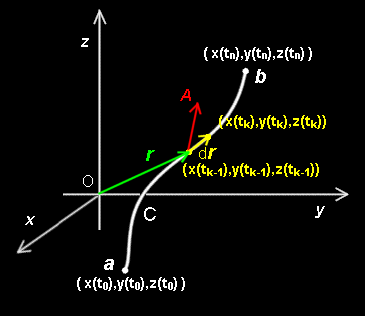

［２］　このとき，パラメータ t で表されるD 内の曲線 C[#]を，

r ＝(x(t)，y(t)，z(ｔ)) ；　　t₀≦t≦t_n　

とします。この曲線上のベクトルA (r ) の線積分をつぎのように定義します。

［３］　まず，t の区間 ［a，b］を n 個の区間に分割し，それを，

　　［a=t₀，t₁］，［t₁，t₂］，･･･，(t_k-1，t_k］，･･･，(t_n-1，b＝t_n］

とします。また，次の記号を導入します。　

Δt_k ＝ t_k−t_k-1　　
 T_k　≡t_k-1≦T_k≦t_k　なる任意の点 t　
 h  ＝ Max(Δt_k)
Δx_k ＝ x(t_k)−x(t_k-1)　　　；　x_k＝x(T_k)
Δy_k ＝ y(t_k)−y(t_k-1)　　　；　y_k＝y(T_k)
Δz_k ＝ z(t_k)−z(t_k-1)　　　；　z_k＝z(T_k)

［４］　そこで，ベクトルA ＝(A₁(x_k，y_k，z_k)，A₂(x_k，y_k，z_k)，A₃(x_k，y_k，z_k) )と Δr_k ＝(Δx_k，Δy_k，Δz_k)との内積を考えて，それを全区間にわたって足し合わせます。ここで，分割の幅をゼロに，すなわち，n → ∞　かつ，h → 0 とした極限が存在すれば，それを曲線 Cに沿ったベクトルA の線積分と定義します。簡潔に書くと，

要するに，dr ＝ (dx，dy，dz) をベクトルとみなし，ベクトルA との内積 A ･dr  を曲線Cに沿って積算していることになります。もし，A が力学的な力を意味しているならば，この線積分によって，

「質点を曲線 C に沿って，a から b まで運ぶときに力A がなす仕事」

を計算することができます。物理的な意味をひとつ知っておくだけで，ベクトルの線積分を考える理由やその使い方の理解が深まることと思います。

［５］ 　さらに別の表現を示しておくと，ベクトルA および，r が媒介変数 t で表せるとき，

	A ･dr ＝			A1(t)	dx	＋A2(t)	dy	＋A3(t)	dz		dt
					dt		dt		dt

↓	(A1(t),A2(t),A3(t))と		dx	，	dy	，	dz		との内積とみなして，
			dt		dt		dt

＝			A ･	dr		dt
				dt

特にパラメーター t として，曲線C の弧長s を用いれば，曲線のC の接線単位ベクトル t [#] を使うことができ，

A ･dr ＝  (A ･t )ds

と表せます。ただし，L は曲線Cの長さ (起点からの曲線に沿った距離) です。

また，ベクトル場A がある関数φ(x,y,z) を用いて，A ＝∇φ （＝gradφ）[#] と表せるときは，

A･dr ＝

｛A1(x，y，z)dx＋A2(x，y，z)dy＋A3(x，y，z)dz｝

＝				∂φ	dx＋	∂φ	dy＋	∂φ	dz
				∂x		∂y		∂z

＝			dφ　　　(合成微分の公式を使って。[#])

＝ φ(b )−φ(a )  （曲線Cの始点をa，終点をb　として。）

ここで，「φはベクトル場A のポテンシャル関数」と呼ばれます。詳しくはまたあとで[#]，それからこちらも⇒[#]

(注意)タルブーの定理も参照して下さい。

［６］　線積分の区間に関するの基本的性質

(1)		＝　−		積分区間の反転

(2)		＝		＋		積分区間の分割１

(3)		＝		＋		積分区間の分割２

簡単なので説明はパス。

SUSTAINABLE　TOKIWADAIGAK　SINCE　2002

２．スカラー関数の線積分　

 以下の内容はベクトルの線積分のバリエーションとして形式的に理解できるものばかりです。

　３次元領域 D 内の曲線 C上のスカラー場が，φ(r )，r ＝［x(t)，y(t)，z(ｔ)］ ，a≦t≦b　と与えられているとき，曲線Cの長さは，

	ds＝		｜r '(t)｜dt

で与えられます。もし，曲線とみなせる針金の線密度がφ(r )で与えられているならば，針金全体の重量は，

	φds＝		φ(r (t))｜r '(t)｜dt

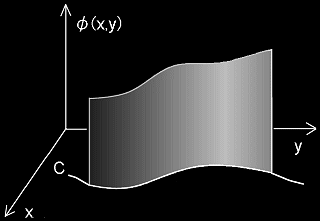
で計算できます。曲線Cを２次元のxy平面内にとり，z＝φ(x,y) とすれば，この線積分，

φ(x(s)，y(s) )ds

は右図のカーテン状の曲面積に等しく，幾何学的な理解もできます。

３．ベクトル関数のベクトル積型の線積分

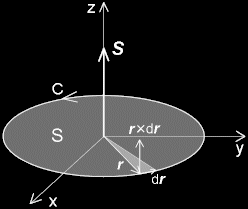ベクトル場A (r)に対する曲線C上の線積分，

	A (r) ×dｒ ＝			A (r(t)) ×	dｒ		dt
					dt

を定義すると，これは擬ベクトルです。たとえば，右図の円周C上の積分，

S ＝	1		（r ×dｒ ）
	2

は円の面積｜S｜＝πr² と同じ大きさをもち，C面の垂直方向 (z図のz方向) と同じ方向をもつ擬ベクトルです。電磁気学ではビオ-サバールの法則を利用した問題を解くときにしばしば使われます。

４．ポテンシャル

［１］ 力学，電磁気学などで，

「　あるベクトル関数(力など)の任意のループ( 閉曲線 )に沿った線積分の値が0 である場合，その関数にポテンシャルが存在する。」

という言い方がされます。これがどういったことなのか説明します。(ちょっとくどいですが，･･)

［２］ まず，仮定としてa　から出発してa に戻る任意のループ C に沿った A(r ) の線積分の値が 0 であるとします。つまり，

	A(r)dr　＝0

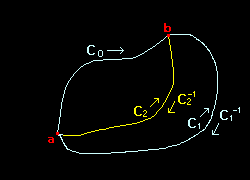
とします。今，ループ C として，右図の白い曲線で表されるような点 b を経由する
C ＝ C₀ ＋ C₁^-1 を考えれば，

	A(r)dr　＝		A(r)dr ＋		A(r)dr　＝ 0

と書けます。また，別の任意のループ，C₀＋C₂^-1 についても同様で，

	A(r)dr ＋		A(r)dr　＝ 0

この２式を比較すれば，共通の　C₀　上の積分項が落ちて，

	A(r)dr ＝		A(r)dr	⇔		A(r)dr ＝		A(r)dr

とわかります。ここで，経路　C₁，C₂ は任意なのでこの等式は，a　から b への線積分は経路によらず，始点a，と終点b だけで決まることを意味しています。したがって，積分値は位置a，b だけを変数とする適当な関数： G(a,b ) で表せます。

［３］　さらに，積分経路を a→b から b→a に反転させれば，積分値の符号が逆転する[#]ことから，G(a,b )＝−G(b,a )を満たす必要があります。これは，ある関数 F を用いて，G(a，b )＝ F(b )−F(a )　と書き換えられることを意味します。つまり，

	A(r)dr　＝ F(b)−F(a)  　　　　←a，b の反転に対して符号が逆転

と書けます。特に積分の始点を，F(a ) ＝ 0　となる点に定め，b をr に表記を改めた位置の関数：F(r )を物理学ではポテンシャル関数と呼びます。   (ストークスの定理 [#] も参照してください。)

A(r)dr　＝F(r)　　　　：  ポテンシャル関数

　この状況は，

「１変数関数 f(x) が ”定積分” 可能なときは，原始関数 F(x) が存在して，そこに始点，終点の値を代入した差

f(x)dx ＝ F(b)−F(a)　　　　(微分積分法の基本定理)

でもって定積分の計算ができる。」

ということの　”(３次元の)多変数関数版”　なのです。

［ 目次へ ］