| 10�@�X�g�[�N�X�̒藝 | |
| f-denshi.com �m�ڎ��ցn�@�ŏI�X�V���F04/05/11 | |
| �T�C�g���� | |
�m�P�n�@�P��Ȑ�C�ň͂܂ꂽ�Ȗ�S ���C�Q�̔}��ϐ� u�Ct �̃x�N�g��������
r ��(x(u,v),y(u,v),z(u,v))��r (u,v)
�ŕ\�킵�Cx�Cy�Cz �� u�Cv �ɂ���C2���̊��Ƃ��܂��B���̂Ƃ��C�ʐϕ��Ɛ��ϕ��Ƃ𑊌݂ɕϊ����鎟�̒藝�����藧���܂��B
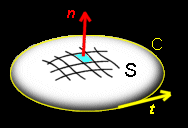
| �X�g�[�N�X�̒藝 �@�P��Ȑ�C �ň͂܂ꂽ�Ȗ�S��Œ�`���ꂽC1���̃x�N�g�����F �@ �@A ��(A1(x,y,z),A2(x,y,z),A3(x,y,z))�C �ɑ��āC
�m�������W�ł̐����\���n ����͋Ȗʂ̊e�_�ł̒P�ʖ@���x�N�g���Cn ��(n1,n2,n3) ��p���Đ����ŏ����C
�܂��C���̎��͎��̂R�̎��𑫂����킹�����̂ł���B
|
 �X�g�[�N�X�̒藝�̕����I�ȈӖ��ɂ��ẮCAppendix�R�@�O�p�`�̃X�g�[�N�X�̒藝�@�Ő������Ă��܂��̂ŁC��������Q�l�ɂ��Ă��������B
�X�g�[�N�X�̒藝�̕����I�ȈӖ��ɂ��ẮCAppendix�R�@�O�p�`�̃X�g�[�N�X�̒藝�@�Ő������Ă��܂��̂ŁC��������Q�l�ɂ��Ă��������B
(�ؖ�)�@�@���@�}��ϐ�u,v ���o�R���ďؖ����܂��BS�ɑΉ����� uv��Ԃ̗̈��U�C���̋��E�� C1�Ƃ��܂��B
�L�E�ȋȖ�S��̔C�ӂ̕Ȑ���C �Ƃ���Ƃ��Cn dS��(ru�~rv)dudv ��p�����[#]�C�藝�́C
�@���Ӂ@���@ rotA �ndS�@ �@�@�@�� rotA �(r�@u�~r�@v)dudv�@
�@�@�� ��A3 �| ��A2 (yuzv�|zuyv)�{ ��A1 �| ��A3 (zuxv�|xuzv) ��y ��z ��z ��x
.�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{ ��A2 �| ��A1 (xuyv�|yuxv) dudv�@�������@[*] ��x ��y
�@�������C�eAk �͕ϐ�xyz�̊��Ƃ��ė^�����Ă���̂ŁC�ϐ�u,v �ɂ��Ă̐ϕ��͂��̂܂܂ł͎��s�ł��܂���B�����ŁC[*]�̔�ϕ�������CA1 ���W����Q�̍��������o���Ď��̂悤�Ɏ���ό`���܂��B
�@�@�@�@ ��A1 (zuxv�|xuzv)�| ��A1 (xuyv�|yuxv) ��z ��y
�@�@�@�� ��A1 yu�{ ��A1 zu xv�| ��A1 yv�{ ��A1 zv�@ xu ��y ��z ��y ��z
�@�@�@�� ��A1 xu�{ ��A1 yu�{ ��A1 zu xv�| ��A1 xv�{ ��A1 yv�{ ��A1 zv xu ��x ��y ��z ��x ��y ��z
�@�@�@�� ��A1 xv�| ��A1 xu�@�@�@�@�@�@���@�������̔�������[#]��p���܂����B ��u ��v
�����ŁCx(u,v)��C2���Ȃ̂ŁCxvu��xuv �ł��邱�Ƃɒ��ӂ���[#]�CA1�Ɋւ��鍀��ϕ�����ƁC
�@�@�ˁ@ ��A1 �@xv�| ��A1 xu dudv ��u ��v
�@�@�@�� ��A1 �@xv�{A1xvu�|A1xuv�@�| ��A1 xu dudv ��u ��v
�@�@�@�� �� �@(A1xv)�| �� �@(A1xu) dudv ��u ��v
���@�O���[���̒藝[#]��p���āC(��U��C1))
�@�@�@�� �@(A1xu)du�{(A1xv)dv
�@�@�@�� A1 (xudu�{xvdv) �@�@�@��(���)��x (u,v) �̑S�����ɂȂ��Ă܂��B
�@�@�@�� A1dx
A2�CA3�@�Ɋւ���ϕ������l�ɋ��܂�C���ǂR�̎������v����ƁC
�@���Ӂ@[*]�@���@ (A1dx�{A2dy�{A3dz)�� A�dr
�ƂȂ�܂��B
|
�@
�ɂ����āCB�@�ˁ@rotA�@�Ƃ�����Cdiv�rotA��0�@�Ȃ̂�
�����藧���܂��B���܁C���̕��Ȗʂ��E�}�̂悤�ɒP��Ȑ�C�ɂ���ĂQ�̋Ȗ�S1��S2�ɕ����čl���܂��B�����ŕȐ���}�̂悤�ɒ�߂�Ɩ@���̐��̌�����S2�̗̈�ɂ����Ă͕����O�Ɗr�ׂ�180�����]���邱�Ƃɒ��ӂ��ĉ������B[#]���ǁC ���Ȃ킿�CC �����Ƃ���C�ӂ̋Ȗ�(S1�CS2)�ɂ����C �ƂȂ�܂��B |
�m�P�n �X�g�[�N�X�̒藝�̊ւ��d���C�w���Ŏg����d�v�Ȓ藝�������Ă����܂��傤�B
| �x�N�g�����@A ���mA1(x,y,z),A2(x,y,z),A3(x,y,z)�n �ɂ��Ď��̂R�͓��l
(�P) �C�ӂ̕Ȑ� C �ɂ�����cA �dr ��0�@�@�@�@ (�@r �� ( x,y,z)�@) (�Q) A ���ރӁ�grad �� �ƂȂ�X�J���[���� �����݂���B�@�m �|�e���V�������̑��� �n (�R) �˂ɁCrotA ��0 |
(�˂ɁCrotA ��0 �̂Ƃ��A�x�N�g����A �� �����̂Ȃ��x�N�g���� �Ƃ����܂��B�܂��C(�Q)�̏������݂����Ƃ��CA ���|�e���V�������Ƃ����܂��B)
(�ؖ�)
(�P)��(�Q)
�}��ϐ�t ��p���Čv�Z���邽�߂ɁC�ʒu�x�N�g�����C
r ��(x(t),y(t),z(t))�@�@
�ƕ\�����Ƃɂ��܂��B�܂��C���銊�炩�ȋȐ� C �̎n�_�� o ��(x(0),y(0),z(0))�C�I�_�� r ��(x(t),y(t),z(t)) �Ƃ��܂��B���̂Ƃ��C(�P)�Ȃ����X�J���[����(r) �����݂��āC[#]
��(r )�� A�dr �� A1 dx �{A2 dy �{A3 dz dt dt dt dt
�����藧���܂��B���̗��ӂ� t �Ŕ�������C
�݃� � dx �{ �݃� � dy �{ �݃� � dz �� A1 dx �{A2 dy �{A3 dz ��x dt ��y dt ��z dt dt dt dt
���ꂪ�C�ӂ̋Ȑ� C��Ő������邽�߂ɂ́C
�݃� ��A1(t)�C �݃� ��A2(t)�C �݃� ��A3(t)�@�@�́@�@A ���ރ� ��x ��y ��z
���������Ȃ�������܂���B
(�Q)��(�R)�@�ؖ��ς݁mrot grad �Ӂ�0�@[#]�@�n
(�R)��(�P)�@�X�g�[�N�X�̒藝��(�R)�� rotA ��0�@���g���ƁC
�@A�dr �� rotA �dS ��0�@
�ȏ�C�����܂��B