Appendix２　四面体のガウスの定理
f-denshi.com   ［目次へ］　最終更新日：03/05/14
サイト検索

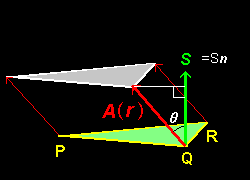
［１］　３次元の領域の中において，速度 A  で非圧縮性の気体が一様に流れている様子を考えます。これをベクトル場：A (r)＝A ＝ 一定 と考えることができます。単位時間に右図の△PQR面を通って流れる気体の量は右の三角斜方柱の体積：M0 と等しいことがわかります。すなわち，

M0＝［△PQRの面積：S］× ［ 高さ：h＝A･n］

で計算できるはずです。ここで，n は三角形PQRの面に垂直な方向を向く単位法線ベクトルですが，これに△PQRの面積を乗じた　面積ベクトル：S ＝Sn　を用いれば，M0は内積：

M0＝S ･A　　　　　　　(h ＝｜A ｜cosθ)

で表すことができます。

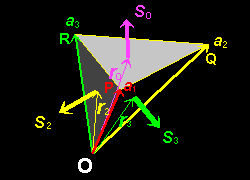［２］　したがって，気体が右図のような四面体OPQR内部から外部へ流出する正味の量 M は，それぞれ４つの面から外への向かう流量を上の方法にしたがって計算し，合計すればよく，

M＝S0･A(r0)＋S1･A(r1)＋S2･A(r2)＋S3･A(r3)

となります。任意のベクトル場A  に対して，このように計算される量 M を束といいます。
(以後この呼び名を用いましょう。)

A が位置の関数である場合でもA の変化が僅少とみなせるほど小さな三角形を考えれば，三角形の重心 rg におけるA の値：

A  (r)＝A (rg) ＝ 一定

を用いることにすれば，ここでの議論は一般化することができます。

［３］　さて，計算をさらに進めるために，この束を頂点Oから頂点P，Q，Rへ向かうベクトル a1，a2，a3 を用いて表しましょう。まず，四面体の各面の面積ベクトルはベクトル積 ”×” を用いて，

S0＝ {(a2−a1)×(a3−a1)}/2
　＝(a2×a3＋a3×a1＋a1×a2)/2
S1＝(a3×a2)/2
S2＝(a1×a3)/2
S3＝(a2×a1)/2　　　

となります[#]。　これから，

S0＋S１＋S2＋S3＝0

はすぐにわかりまね。

［４］　一方，各三角形の重心をしめす位置ベクトルは，

△PQRの重心：　r0 ＝ (a1＋a2＋a3)/3
△OQRの重心：　r1 ＝ r0−a1/3
△ORPの重心：　r2 ＝ r0−a2/3
△OPQの重心：　r3 ＝ r0−a3/3

となります。　以上で準備は整いました。これから四面体のガウスの法則を導きます。

［５］　ベクトル場としては，Appendix 1 で説明した線形ベクトル場，すなわち，3次正方行列Aを用いて，

A(rk)＝Ark＋B 0 ； (k＝0，1，2，3) ，B 0：定行列

と近似できる[#] 場合を考えましょう。すると，束 M は，

M　＝S0･Ar0＋S1･Ar1＋S2･Ar2＋S3･Ar3＋(S0＋S１＋S2＋S3)･B 0
　　＝S0･Ar0＋S1･A(r0−a1/3)＋S2･A(r0−a2/3)＋S3･A(r0−a3/3)
　　＝(S0＋S1＋S2＋S3)･Ar0　−{S1･Aa1＋S2･Aa2＋S3･Aa3}/3
　　＝−{S1･Aa1＋S2･Aa2＋S3･Aa3}/3
　　＝−{(a3×a2)･Aa1＋(a1×a3)･Aa2＋(a2×a1)･Aa3}/6
　　＝　{b1･Aa1＋b2･Aa2＋b3･Aa3}･V四面体
　　＝ (ｔｒA)･V四面体

ただし，
b1＝ a2×a3 ，b2＝ a3×a1 ，b3＝ a1×a2
［a1a2a3］ ［a1a2a3］ ［a1a2a3］

であり，　
　　　　　　am･bn＝δmn　　

を満たします。{b1，b2，b3}は，{a1，a2，a3}の相反基底 です[#]。また，［a1a2a3］ はスカラー三重積[#]で，この３つのベクトルが作る平行６面体の体積，またはこのベクトルが作る四面体の体積 V四面体 の６倍です。

［６］　また，最後の ”＝” の後の(trA)は行列A の対角成分の和 ［ トレース ］ を意味します。なぜなら，{a1，a2，a3 }を基底として成分を表示すると，

a1 ＝ 1 ， a2＝ 0 ， a3＝ 0
0 1 0
0 0 1
b1＝(1 0 0)，b2＝(0 1 0)，b3＝(0 0 1)，
A ＝ a11　a12　a13
a21　a22　a23
a31　a32　a33

と表現でき，{b1･Aa1＋b2･Aa2＋b3･Aa3}の第１項の計算は，

b1･Aa1＝(1 0 0) a11　a12　a13 1 ＝a11
a21　a22　a23 0
a31　a32　a33 0

となります。同様に第２項，第３項から，a22，a33　がでてきます。結局，

b1･Aa1＋b2･Aa2＋b3･Aa3＝a11＋a22＋a33≡trA　

と書くことができます。

［７］　線形ベクトル場：A (r)＝［A1(x，y，z)，A2(x，y，z)，A3(x，y，z)］の場合，

ｔｒA＝ ∂A1 ＋
∂A2 ＋ ∂A3
∂y ∂z
∂x

なので[#]，ベクトル場の小さな四面体において成り立つ関係は次のように書けます。

四面体の発散定理：  (極小サイズ)
Ak･Sk＝ ∂A1 ＋
∂A2 ＋ ∂A3 ･V四面体
∂y ∂z
∂x
左辺の和は四面体の４つの面について和をとることを意味します。

ふつうサイズの多面体は必要なだけ小さな四面体に分割することができるので，上で得られた式を多面体を構成する四面体の数だけたし合わせれば「多面体の発散定理 」となるはずです。その際，多面体の内部にある面は隣り合う四面体どおしで共有しており，その法線ベクトルは180°反対を向いています。したがって，多面体内部にある面が内積Sk･Akに寄与する項はキャンセルし合ってゼロとなります。以上のことから，

ふつうサイズの多面体の発散定理

Σ (Ak･Sk)＝ Σ ∂A1 ＋
∂A2 ＋ ∂A3 ･A四面体T
∂y ∂z 四面体T
多面体表面 各四面体 ∂x

となります。Σ各四面体　は多面体を構成する(分割された)四面体 T；(T＝1，2，････)すべてについて和をとることを意味しています。

＊　参考のために一般的なガウスの定理を示すと，

A ･dS  ＝ divA dV

となっております。(もちろんこれは「 ふつうサイズの多面体の発散定理 」を微積分の記号に置き換えた表しただけです！)

［ 目次へ ］