| 5 電気双極子と電気四重極子 | ||
| f-denshi.com [目次へ ] 最終更新日: 21/10/20 | ||
| サイト検索 | ||
ここでは数個のプラス-マイナス等しい数の電荷が作る電場や相互作用について考えます。身の回りの多くの物質は見かけ上電気的に中性であっても,分子レベルでは電荷の偏り(永久双極子モーメント)が存在し,これが液体の粘性や固体の強度のような集合体としての特徴を作り出しています。例えば水分子は全体として中性ですが,水素に較べて酸素原子上に電子が偏在しており,水素原子はプラス,酸素原子はマイナスに電荷を帯びています。その結果,水は分子量の割に粘性が高い,沸点が高いなどの性質を持っているのです。一方,不活性ガスのアルゴン原子のように球称性を持っている原子分子は永久双極子モーメントをもっていませんが,そのような分子でも電場の中に置かれると,電子と原子核はそれぞれ反対方向に力を受け,分極(誘起双極子モーメント)が生じます。このように電気双極子は物質の性質を決めるもっとも重要な因子のひとつです。
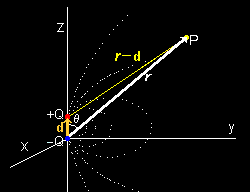 [1] 右図のように ”極く近い距離にある等しい正負の電荷の対” を電気双極子といいます。
[1] 右図のように ”極く近い距離にある等しい正負の電荷の対” を電気双極子といいます。
(原点に -Q の電荷,z軸方向 d の位置に +Q の電荷,d=dez ,ez : z方向の単位ベクトル)
電気双極子が位置Pに作る静電ポテンシャル φ は重ね合わせの原理から各電荷のポテンシャルの和として,
4πε0φ= -Q + Q |r| |r −d|
≒ -Q + Q + Qr ・d | r| |r| |r|3
= Q(r ・d ) |r|3
とテーラー展開できます。導出は多重極子展開参照のこと⇒[#] 。
ここで,電気双極子モーメントを,p = Qd と定義すると,
φ(r)≒ 1 r ・p = p cosθ ≡φ(r,θ) [球座標] 4πε0 |r|3 4πε0 r 2
ただし,p =|p |,r =|r |,r ・p=pr ・ez=pr cosθ
[2] 電場 E はこの勾配から位置ベクトルの微分公式,
(1) ∇rn = n rn-2r
(4) ∇(r ・a ) = a ( a : 定ベクトル )
を用いて,[#]
E (r ) ≒ −∇ φ
= − (r ・p) ∇ 1 − ∇(r ・p ) 4πε0 r 3 4πε0 r 3
= 1 3(r ・p)r −p [直交座標] 4πε0 r 3 r 2
および,球座標表示の φ(r,θ)を微分して[#],
Er = − ∂φ(r,θ) = 2p cosθ ∂r 4πε0 r 3
Eθ =− ∂φ(r,θ) = p sinθ [球座標] r∂θ 4πε0 r 3
となります。
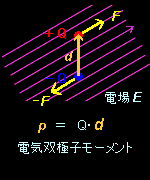 [1] 一様とみなせる電場 Eの中に置かれた電気双極子 p が受ける力 F は偶力(大きさが等しく一つの直線上にない反対方向を向く力)で,力のモーメントN は,
[1] 一様とみなせる電場 Eの中に置かれた電気双極子 p が受ける力 F は偶力(大きさが等しく一つの直線上にない反対方向を向く力)で,力のモーメントN は,
N = r×(-F )+ ( r + d )× F
= d × F
= d × QE
= p × E
となります。N は画面の奥へ方向へ向かうベクトルです。後で使います ⇒ [#]
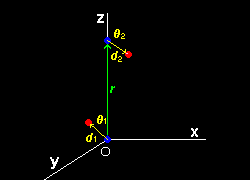 [1] 2つの同種の双極子モーメント間の静電相互作用によるエネルギー U を計算します。
[1] 2つの同種の双極子モーメント間の静電相互作用によるエネルギー U を計算します。
|
d1 = ( d1x,d1y,d1z ) |
として,
| 4πε0U = Q2 | 1 | − | 1 | − | 1 | + | 1 | ||
| |r| | |r −d1| | |r +d2| | |r +d2−d1| |
| ≒ Q2 | − | r・d1 | + | (r +d2)・d1 | ||
| |r|3 | |r +d2|3 |
| = Q2 | − | r ・d1 | + | 1 | − | (r ・d2) | 3 | (r +d2)・d1 | ||||
| |r|3 | |r| | |r|3 |
| = Q2 | − | r ・d1 | + | 1 | − | 3(r ・d2) | + | 3(r ・d2)2 | − | (r ・d2)3 | (r +d2)・d1 | ||||
| |r|3 | |r|3 | |r|5 | |r|7 | |r|9 |
| = Q2 | d1・d2 | − | 3(r ・d2)(r +d2)・d1 | + | 3(r ・d2)2 | + | (r ・d2)3 | (r +d2)・d1 | |||||
| |r|3 | |r|5 | |r|7 | |r|9 |
| = Q2 | d1・d2 | − | 3(r ・d2)(r ・d1) | +O(r-4) | |||
| |r|3 | |r|5 |
| = | p1・p2 | − | 3(r ・p2)(r ・p1) | +O(r-4) | ||
| |r|3 | |r|5 |
ここで,O(r-4})はr-4以上の高次の微小項のことです。この相互作用は双極子間距離の3乗に比例して小さくなっていきますので,クーロンポテンシャル(r-1)に比べてごく近距離においてのみ働く力(相互作用)だとわかります。
この結果は,pkが磁気双極子 [#] の場合においても同様の形式を与えますが,その際,ε0はμ0に置き換えます。
さらに磁気双極子が分子電流 (電荷の円運動,遠方から見れば自転) で置き換えられること [#] を考慮すれば,電子や原子核のスピン-スピン相互作用に対する表式 (ハミルトニアン) にも対応させられるだだろうことは容易に推測できます。
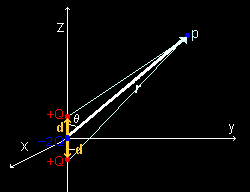 [1] 右図のように,−2Qの電荷が原点にあり,そこからz軸方向±d の位置に+Qの電荷がある配置(電荷の符号は逆でもよい)を電気四重極子といいます。この電気四重極子が遠方に作る電位を求めてみましょう。
[1] 右図のように,−2Qの電荷が原点にあり,そこからz軸方向±d の位置に+Qの電荷がある配置(電荷の符号は逆でもよい)を電気四重極子といいます。この電気四重極子が遠方に作る電位を求めてみましょう。
原点から観測点Pを示す位置ベクトルをr,この位置ベクトルとz軸とのなす角度をθとします。また,正電荷の位置を示すベクトルを,±dとすると,正電荷から点Pを指すベクトルは,
r1 = r −d
r2 = r +d
となります。ここで, 1/r1 を展開すると
| 1 | = | 1 |
| r1 | (r2−2rdcosθ+d2)1/2 |
| = | 1 | 1 | |||
| r | (1−(2d/r)cosθ+(d/r)2)1/2 | ||||
| = | 1 | 1− | 1 | −(2d/r)cosθ+(d/r)2 | + | 3 | −(2d/r)cosθ+(d/r)2 | 2 | ・・・・・ | ||||||
| r | 2 | 8 | |||||||||||||
| = | 1 | 1+(d/r)cosθ+ | (3cos2θ−1) | (d/r)2 +・・・・ | |||
| r | 2 | ||||||
同様に
| 1 | = | 1 | 1−(d/r)cosθ+ | (3cos2θ−1) | (d/r)2 +・・・・ | ||
| r2 | r | 2 | |||||
よって,電気四重極子の形成する電位は,
φ = 1 Q + Q + -2Q 4πε0 r1 r2 r
= Q d2(3cos2θ−1) 4πε0r3
= Q d2(3z2−r2) 4πε0r5
ここで,
3z2−r2=(x,y,z) -1 0 0 x 0 -1 0 y 0 0 +2 z
と行列計算で表されることに注意すれば,電気四重極子の電気ポテンシャルは,
φ = r ・Qr 4πε0r5
ただし,
Q=Q d2 -1 0 0 0 -1 0 0 0 +2
は電気四重極テンソルと呼ばれます。 (一般論として,多重極展開と呼ばれるものがあります。[#])
したがって,遠方に形成される電気四重極子の電場は,
Er = − ∂φ(r,θ) = 3Q d2(3cos2θ−1) ∂r 4πε0 r 4
Eθ=− ∂φ(r,θ) = 6Q d2cosθsinθ r∂θ 4πε0 r 4
極座標表示の電気双極子の作る電場を直交座標系の結果から座標変換して求めてみます。
なお,デカルト座標と極座標表示で使用される変数の関係 [#],
x = r sinθcosφ
y = r sinθsinφ
z = r cosθ
に注意して,まず,デカルト座標系の電場は:
E = 1 3(r ・p)r −p 4πε0 r 3 r 2
= 1 3p cosθr −p ・・・・ (1) 4πε0 r 3 r
と書き直せます。これを球座標への基底変換,
ex=sinθcosφer+cosθcosφeθ− sinφ eφ
ey=sinθsinφer+cosθsinφeθ+ cosφeφ
ez= cosθer − sinθeθ ・・・・ (2)
を行うと,
(1)の( )の第1項の極座標表示は,r=rer より,
3p cosθr =3p cosθer r
( )の第2項のp=pez の極座標表示は(2)より,
p=p(cosθer−sinθeθ)
したがって,極座標表示の電気双極子の作る電場を,E=Erer+Eθeθ+Eφeφとすると,
Er = 2p cosθ 4πε0 r 3
Eθ= p sinθ 4πε0 r 3 Eφ=0
と求まります。