| 11 磁化と磁荷 | ||
| f-denshi.com [目次へ] 最終更新日: 21/10/25 | ||
| サイト検索 | ||
巨視的現象論である電磁気学では,いわゆる永久磁石の作る磁場の解釈として,(1)微視的な磁気双極子によって作り出される磁場,(2)微視的な円電流によって作り出される磁場の2通りの解釈があって,これらが等価であることをこのページでは示します。
実際は,「微視的」には,単磁荷の存在はいまだ確認されず,(分子サイズの) 円電流も電磁波を放出し続けてエネルギーを失ってしまうために安定に存在できず,どちらも正しくありません。そういう意味で,EH対応とEB対応の優劣を議論することは不毛なこととも思えます。
微視的に現象を説明するためには量子力学による記述が必要となります。
歴史的には永久磁石の示す磁性の方が電流のつくりだす磁性よりずっと古くから知られていました。また,静電気現象も古くから知られていましたが,近年までこれら二つは全く別の現象と考えられてきました。しかし,電流に磁石が応答することをエルステッドが発見した(1820年)ことで,この2つの現象が結び付けられました。精密な磁気測定が可能な現在では,磁石だけでなくすべての物質が磁場の中で,その影響を受けることがわかっています。
 [1] 永久磁石の作る磁場は電流の作る磁場と異なる機構に基づいて発現するように見えますが,原子一個一個に流れる分子電流の作り出す磁場として考えることで統一的な理解(電流こそが磁場の源であるということ!)が可能なことをここでは示します。
[1] 永久磁石の作る磁場は電流の作る磁場と異なる機構に基づいて発現するように見えますが,原子一個一個に流れる分子電流の作り出す磁場として考えることで統一的な理解(電流こそが磁場の源であるということ!)が可能なことをここでは示します。
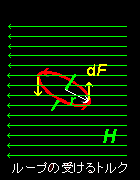
物質の示す磁性を説明するためにアンペールは,分子を円電流の集合で置き換えられるのではないかと考えました。右図のように均一な磁場の中におかれた一つの小さな円電流を考えると,微小な円弧 dsに働く力はフレミングの左手の法則[#]に従い,
dF =I ds×μ0H
で与えられます。この力は円の中心に対して対称的な位置では互いに反対向きで大きさが同じです。一般的にこの作用線は円の中心(重心)を通らないのでリングにはトルク(偶力)が生じます。まず,このトルクを計算して見ましょう。
[2] 位置r の電流要素に働くトルク dN は,r ×dF なので,これを電流ループ全体について積分すればいいワケです。一般性を失うことなく円電流,磁場の方向を下図のような座標に取って計算を行なえます。
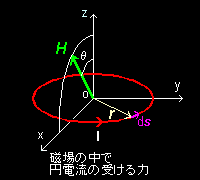
N = (r ×dF ) = I ・ r × ( ds×μ0H )
↓ ここの計算はちょっとわかりにくいので,下に計算方法を示しました。計算→[#]
= I (r ×ds )×μ0H 2
↓ 1 (r ×ds )=S とおいて 2
N = IS ×μ0H [電流ループに働くトルク] ・・・・・[*]
と計算できます。 ここでS は円の面積ベクトルで,円板に垂直で(図中のz方向),大きさは円の面積と等しいものです。
(線積分経路ループC上で)r と ds は常に直交しているので,| S | = (1/2)r ・ 2πr =円の面積です。)
[3] この円電流をマクロな物理量と関係づける流儀が2通りあります。その1つは,
| μ0IS =m [Vs(A・m)-1][A][m2]=[Vsm] (磁気双極子モーメント) − EH対応 − |
とおいて話を進めていく方法で,トルク[*]は,
N =m × H
となります。いま,これを均一な電場中におかれた電気双極子モーメントp が受けるトルク[#],
N =p × E ← 電場中の電気双極子の受けるトルク
と比較すると数学的な形式が同じだとわかります。つまり,磁気現象の記述に静電気学の取り扱い方をそっくり ”まねる” ことができる(注意)わけです。そこで電気双極子モーメントp に対応させて,m [Vsm] を磁気双極子モーメント(または磁気双極子) と呼ぶことにします。このような取り扱い(定義)では電場 E と磁場 H が対応しているので,EH対応と呼ばれます。
[4] 一方,磁気双極子モーメントを,
| IS = mB [Am2] (磁気双極子モーメント) − EB対応 − |
と定義して,トルク[*]を,
N = mB × μ0H
= mB ×B (ただし,B =μ0H )
と記述する方法も可能です。このmB は双極子と呼ぶより,分子電流と呼ぶにふさわしい量です。この場合,静電気学と比較する際,数学的に電場E と磁束密度B が対応しています。これをEB対応といいます。この場合,よけいなパラメーターμ0 が入っておらず,mB [Am2] の物理的な意味は明快です。
| 磁気双極子モーメントの2つの定義 | ||
| (1) EH対応 | p ⇔ m (=μ0mB) [Vsm] | E ⇔ H |
| (2) EB対応 | p ⇔ mB [Am2] | E ⇔ B |
このように電磁気学の構成の仕方には2つの方法がありますが,この講義ではもっぱらEH対応で説明します。しかし,どちらの「対応」もよく使われているのでいろいろな文献を読むときには注意が必要です。
[5] 電気双極子が符号の異なる電荷±Qとその負電荷から正電荷へのベクトルd を用いて
p ≡ Qd [C・m]
と表せるように,p とm が対応する EH 対応においては,電荷 ±Q に対応する物理量として,磁荷 ±Qm を導入し,磁気双極子モーメントを,
m ≡ Qmd [ 磁荷の定義式 ]
と記述し,静磁気学の出発点に磁荷を位置づけることも可能です。このとき磁荷 Qm の単位 [?] は,
μ0IS=m =Qmd [#]
の単位を比較して,
([V][s][A・m]-1)・[A]・[m]2 = [V][s][m]=[?]・[m]
となる[#] ので,[?]=[V・s] が磁荷 Qmの単位です。しかし,磁荷は電荷[C]に対応(匹敵)する重要な物理量なので,
[Wb]=[V・s] [Wb] ← ウェーバー と読む
という単位を導入(定義)して磁性現象の単位のひとつとして用いることにしましょう。
[4] 磁荷 Qm に関しては,後に示すように [#] 電荷と同じようにクーロンの法則が成り立ち,静電気学の成果をそのまま利用することが可能です。ただし,数学的にプラス,マイナスの磁荷を仮定して合理的な体系を作ることが可能なことと磁荷が実際にプラス・マイナスそれぞれ単独で存在していることは違います。実際,現在まで磁荷はいつもプラス・マイナスが ”対”(磁気双極子として)の状態でしか見出されていません。
[1] 磁気モーメントの巨視的な集団を考えるときは静電気学の ”分極” [#]に相当する磁化を,
「単位体積中の磁気モーメントの総和」
と定義すると便利です。単位体積中の磁気モーメントの数を n [m-3] とすると,
M = n × ( m,またはmB )
で与えられます。磁化はEH対応,EB対応のどちらか,つまり,m と mB のどちらを採用するかで値(単位)が違ってきます。
[2] [EH対応における磁化M ]
EH対応では,m (=Qmd ) [Wb・m]より,M の単位はこれを [m-3] を乗じた[Wb・m-2]です。これは単位面積あたり[m-2]の磁荷[Wb]なので,”磁荷密度”と呼ぶべきような量だとわかります。さらに静電気学で電荷密度という物理的な意味をもつ分極P [C/m2] が電束密度(電気変位)D [C/m2] と対応したように[#],磁化M [Wb・m-2] は磁束密度B [Wb・m-2] [#] に対応していることを示しています。すなわち,
M ⇔ B [V・s・m-2]=[Wb・m-2]
なる対応があります。また,電気分極P にも対応することからM を磁気分極とも呼ぶこともあります。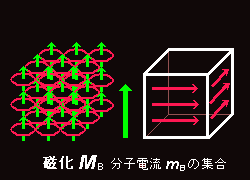
[3] [EB対応における磁化MB]
EB対応の場合ですが,磁化MBはmB(分子電流)の集合(総和)で右図のように考えることができます。MBの単位は[Am2]・[m-3]=[Am-1],つまり,磁場H [#]と同質のものであることがわかります。視覚的には物質の磁化を右図のように磁性体の側面に流れる電流の作る磁場[A・m-1]と見なすことができるのです。すなわち,
MB ⇔ H [A・m-1]
なる対応が見られます。
ここで,アンペールの法則の微分形: j = rotH を思い出せば[#],磁化電流密度を
j M ≡ rotMB = rot (M/μ0)
と定義することは自然です。
[4] ここで出てきた物理量の単位について一覧表にしておきましょう。
| 電気 | 電気双極子 | 分極 | 電束密度 | 電気感受率 | 誘電体中で |
| EH,EB 共通 |
p [Cm] | P [Cm-2] | D [Cm-2] | χ =ε0χr [Fm-1] | D =ε0E +P=(ε0+χ)E =ε0 (1+χr)E =ε0εrE |
| 磁気 | 磁気双極子 | 磁化 | 磁束密度/磁場 | 磁気感受率/磁化率 | 磁性体中で |
| EH対応 | m [Wb m] | M [Wb m-2] | B [Wb m-2] | χm =μ0χ'm [Hm-1] | B = μ0H +M = (μ0+χm)H |
| EB対応 | mB[Am2] | MB [Am-1] | H [Am-1] | χ'm [無次元] | B =μ0(H+MB)=μ0(1+χ'm)H =μ0μrH |
ときわ台学(電磁気学,および,物性論)ではEH対応における磁化を簡単にM と表記することにしています。しかし,EB対応を採用している他の教科書(講義)においては,M という表記を上の表のMBに対応させて用い,E-H対応での磁化M に対応する物理量はPm と書いて磁気分極と呼ぶことがあります。しかし,E-B対応を謳いながら磁化に関してだけはM を用いている教科書もあります。また,磁気感受率χmは電気におけるχ,磁化率χ'mは電気におけるχrに対応しています。しかし,この2つの表記法はかなり混同されているので,他の教科書等と比較する場合には,それらがどのように定義されているのか注意が必要です。
ここでは詳しく述べませんが,χmは物質によっては正ではなく負の値をとることがあり,これは電気と磁気の対称性が損なわれているところです。 ⇒ ソレノイドの話題のところで説明する。
[5] さて,これまでみてきたD とB との数学的な対称性を考えると,電荷のガウスの法則[#]に対応して
D ・ndS = Q ⇔
B ・ndS = Qm (=0)
あるいはもっと一般的な曲面に対して,(閉曲面である必要はありません。)
D ・ndS = Ψe ⇔
B ・ndS = Ψm = Qm dΩ 4π
が成り立つ,または定義して利用することが可能です。これらの量は磁荷に対するガウスの法則,または磁束Ψm (⇔ 電束Ψe [#])の定義を与える式となっています。(さらに,電束が考えている面 S を貫く電気力線の本数[#]に比例したように,磁束は同様な磁力線の本数に比例すると考えることもできます。)
[6] ただし,電気と磁気との違いもあります。それは先程述べたように真磁荷は存在しないと考えられているからです。つまり,真磁荷密度ρmなるものを考えてもそれはいつもρm=0 でなければならないのです。
磁荷のガウスの法則 (真磁荷の不存在)div B = 0 [微分形]
|
がえられます。これは電磁気学の基本法則のひとつです。証明は, divD = ρ と同じ[#] であることはいうまでもないでしょう。
[7] 電気双極子と磁気双極子のトルクの数学的な対称性から導かれる「電荷q ⇔ 磁荷qm 」 なる対応関係によって,静磁場H 中に置かれた磁荷qmの受ける力F が,
F = qmH
とかけることや,
|
と記述可能である(=磁荷に対するクーロンの法則が成り立つ)。 |
ことを定式化することができます。
クーロンの法則から静電気学の諸法則を導いた過程(数学的な方程式の変形)や力の計算方法を逆にたどれば,磁荷のクーロンの法則に辿りつくはずです。もちろん,反作用として,Qmには−F の力が働き,重ね合わせの原理も適用できます。
[8] 磁気双極子によって作り出される磁場と微視的な円電流によって作り出される磁場が遠方において一致することを最後に確認しておきましょう。
円電流が作り出す磁場 はすでに導いたように[#], S=πa2,μ0I S=m として,
H r= I a2cosθ = 2μ0Iπa2cosθ = 2m cosθ 2r3 4πμ0r3 4πμ0r3
Hθ= I a2sinθ = m sinθ 4r3 4πμ0r3 ・・・ [**]
と球座標で表されます。
一方,電荷のクーロンの法則から導出される電気双極子p が遠方に作る電場[#]は球座標で,
E r = 2p cosθ 4πε0 r 3
Eθ = p sinθ 4πε0 r 3 ・・・ [***] Q → Qm
⇒
ε0 → μ0
H r= 2m cosθ 4πμ0r3
Hθ= m sinθ 4πμ0r3 ・・・ [**]
と表されます(上記左側)。
この[***]式において,ε0 をμ0 と読み替え,p (=|Qd|)を m (=|Qmd|) に対応させる,すなわち, Q ⇔ Qm と対応させれば,[**] となりますが,この式は,磁荷の存在と磁荷のクーロンの法則とを仮定して導かれた磁気双極子m =Qmd によって作られる磁場になります。
そして,それが円電流によって作られる磁場 [**] と完全に一致することを確認できます。
結論,分子(円)電流の作る磁場と磁気双極子の作る磁場は,巨視的に区別ができない。
ということです。
正規直交座標系で右図のように各ベクトル,
r =(rcosφ, rsinφ, 0 ) |
 |
を配置させると,ベクトル3重積: x ×(y ×z )=(x ・z )y −(x ・y )z [#]を用いて,
N / I =
r×(ds×μ0H)= {(r ・μ0H )ds −μ0H (r ・ds)}
= μ0r2H sinθcosφ( -sinφdφ,cosφdφ,0 )
= μ0r2H ( −sinθcosφsinφdφ,sinθcos2φdφ,0 ) = ( 0,πμ0r2Hsinθ,0 ) 途中より( )にベクトルの成分を並べています。
= μ0r2Hsinθ( 0, cos2φdφ,0 )
一方,
(r×ds)×μ0H = (r ・μ0H )ds −r(ds・μ0H)
= μ0r2H {(sinθcosφ( -sinφdφ,cosφdφ,0 )+sinθsinφdφ( cosφ,sinφ,0 )}
= μ0r2H dφ(0,sinθ(cos2φ+sin2φ),0) = ( 0,2πμ0r2Hsinθ,0 )
= μ0r2Hsinθ(0, dφ,0)
よって,
N =I・ r×(ds×μ0H) =(I/2) (r×ds)×μ0H
ソレノイド (10/06/27)
磁性体 (鉄芯など) をソレノイド中に挿入すると,同じ電流を流しているにも関わらず,形成される磁場は挿入前より強くなります。 (H0→H1,または,B0→B1) この現象を古典電磁気学の範囲で説明する方法には,磁性体をどのように取り扱うかによって,電流モデルと磁荷モデルの2通りがあります。
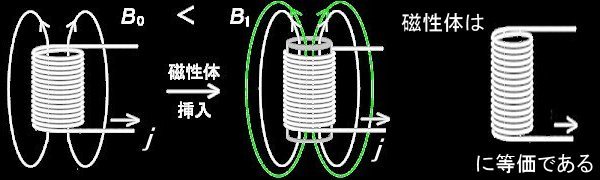
「電流モデル」は,磁性体の中には分子電流が存在し,外部磁場が存在しないときはバラバラの方向を向いているが,磁場の中に置かれると,磁性体中の分子電流が外側の電流と同じ回転方向になるように向きを変えるため,全体として磁場や磁束密度の大きさが増大するという解釈です。この様子を上図中では,磁束を辿る磁束線のループを追加することで表しています。つまり,磁性体の挿入を新たなソレノイドの追加と考えるわけです。
もう一つの「磁荷モデル」は,物質の磁気現象が誘起磁荷によるとの立場に立脚するものです。電場の中に入れられた誘電体が電気分極を生じるのと同様に,磁場の中に磁性体が置かれると,磁性体は磁気分極を起こし,反対負号を持つ磁荷が磁性体の両端に誘起され,その磁荷が形成する磁場の分だけ全体の磁場が強く観察されるとの解釈です。
電荷に対する電気変位D と電気分極P との関係に,磁束密度B と磁化M をなぞらえると,等方的な磁性体が形成する磁束密度は,
B = μ0H +M (1)
と書くことができます。今,考えているような画面の下から上に向かう外部磁場の中に置かれた磁性体に誘起される磁化と磁場,磁束密度の関係を模式的に描くと下図のようになります。
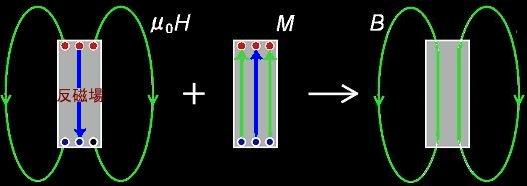
磁化M は,負磁荷,-qmから正磁荷 +qmへ向かうベクトルをd とすると,qmd で定義されます。磁場を辿る磁力線は,正磁荷から生じて,負磁荷で消滅しますが,その一部は磁性体の内部を通ることとなります。この内部に形成される磁場を反磁場と呼ぶことがあります。磁束密度は,磁場と磁荷を(1)にしたがって合成することで得られますが,その結果得られる磁束Bを辿る磁束線はわき出しや吸い込み口のないループを描くことになります。もちろん,これは電流モデルにおいて,磁性体が作り出す追加的な磁束線 (B1-B0) と同一です。つまり,B0+B=B1が成り立っています。
これらは一見,異なる物理的な描像ですが,数学的に等価です。
(1)をHについて解いて,回転をとると,
rot H = rot (B −M )/μ0=0 (真電流密度)
∴ rot B =rotM =μ0j M (〜磁化電流密度)
とアンペールの法則を書くことができます。一方,ソレノイドだけが単独で作る磁場H 0については,
rot H 0= j
∴ rot B 0=μ0j
となります。これら2式をそれぞれ足しあわせると,磁性体の挿入されたソレノイドの磁場,磁束密度は,
rot H 1 = rot (H +H 0) = j
rot B 1 = rot (B +B 0) = μ0 (j+j M )
と表されることとなります。1行目の式は合成した磁場についてもアンペールの法則がそのまま成り立つことを示しています。
ここまでの説明では,磁化率が正の値をとることを前提としたような話の進め方をしてきましたが,物質によっては磁化率が負となるものも存在します。磁化率が負の物質は反磁性体と呼ばれ,不対電子を持たない物質に見い出される特徴です。また,不対電子をもち,磁化率が正の値をとる物質は,その大きさや磁場を取り除いたあとの残留磁化の有無によって,常磁性体,強磁性体の大きく2つに分類することができます。