 |
Appendix 3 連続基底(ブラケット記法) |
| f-denshi.com 更新日: 11/07/27 |
| サイト検索 |
行列力学の具体例として前の2つのAppendixまでは離散的な(とびとびの)固有値,固有関数の取り扱いについて述べてきました。しかし,離散的な固有関数を基底としたのでは,連続的な固有値を持つ物理量,例えば,自由粒子の位置,運動量などは表現できないことは直ぐに想像できます。これらを表すには連続的な基底が必要なのです。
1. 位置演算子
[1] 位置演算子x を,位置固有ケット|x>に作用してその位置という物理情報である固有値 x を得る固有方程式として,
と定義します。これは離散的な固有値をもつ場合と全く同じ見かけの形式です。位置の固有ケットは位置 x を連続的に-∞から+∞まで変化させたすべての固有ケットを考えることができるので,その無限個の集まり全体は,無限次元空間の
''正規直交基底'' と考えることができます。ここで,固有関数(=位置固有ケットによる位置固有ケット |x'>の展開=位置固有ケット |x'>のx-表示(座標表示)とみなせる) は,
とあらわすことができます。δ(x)はデルタ関数で,x=0 のとき ∞,x≠0 のとき 0 の値をとり,-∞≦x≦∞で積分すると1となる関数です[#]。これは離散的な固有値をもつ系において基底 {|a1>,|a2>,・・・,|an>}が,正規直交基底であるならば,
<aj|ak>=δjk
を満足していることを思い出すと,その連続状態への拡張であることが理解できます。しかし,<aj|aj>=1に対して,<x|x>=∞であることには注意せよ。
[2] スピン空間が2つのスピン基底の線形結合で表せたように,位置やその時間変化が関係する任意の物理状態
|ψ>は,
| |ψ>= |
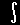 |
d x|x><x|ψ> |
|
と展開することが可能とします。(数学的にはヒルベルト空間L2上で記述可能ということ。これはちょっと高級!離散的固有値の場合からの類推でとりあえずガマン。) すると,これは|ψ>を位置固有ケット|x>で展開したときの展開係数が <x|ψ>
であることを示しています。一般に恒等演算子である,
| I = |
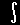 |
d x|x><x| |
|
を演算子の配置可能な位置に挿入できることも離散的な場合と同じです。位置固有ケットによる展開係数:
<x|ψ>≡ψ(x)
は波動関数と呼ばれており,3次元空間での波動関数は
| ψ(r)≡<r |ψ>; ψ*(r)≡<ψ|r > |
また,状態ψが状態φに見出される確率振幅 <φ|ψ> の x 表示は,
| <φ|ψ> |
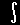 |
dx<φ|x><x|ψ> = |
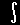 |
dxφ*(x)ψ(x) |
|
|
となります。
2.連続スペクトル
連続固有値 (連続スペクトル) をもつ場合の数学的取り扱いは,離散スペクトルで得た形式から,
| Σを ⇒ ∫dx で置き換える。 (積分範囲は(-∞,∞)) |
とすることで対処が可能です。(厳密な議論は量子力学の初歩を学んだ後に行うが賢明!)
そのための対応関係を表にしておくと次のようになります。連続スペクトルとしては位置r
に使われる記号を用いましたが,pでもOK。
|
離散スペクトル |
連続スペクトル |
| 適用対象 |
有限空間(狭い空間)に閉じ込められた粒子 |
自由空間(かなり広い空間)にある粒子 |
| 固有方程式 |
A|ak>=ak|ak> |
x|x>=x|x> |
| 恒等演算子 |
Σ|ak><ak|=1 |
 |
d x|x><x|=1 |
|
| 状態ケットの展開 |
|ψ>=Σ|ak><ak|ψ> |
| |ψ>= |
 |
d x|x><x|ψ> |
|
| 表示 |
<ak|ψ>=ck |
<x|ψ>≡ψ(x,t)
| <x|ψ>= |
 |
d x'<x|x'><x'|ψ> |
| = |
 |
d x'δ(x−x')<x'|ψ> |
|
| 正規直交性 |
<aj|ak>=δjk |
<x'|x">=δ(x'−x") |
| 規格化 |
Σ|<aj|ψ>|2=1 |
 |
d x|<x|ψ>|2=1 |
|
( x,y,z,(3次元→r ),x,y,z,(3次元→r)と書くことにします。 )
| 波動関数の展開 |
<r|ψ>=Σ<r|ak><ak|ψ>
ψ(r) =Σφk(r) ck |
| <r|ψ>= |
 |
d r'<r|r'><r'|ψ> |
| ψ(r) = |
 |
d r'δ(r'−r)ψ(r',t) |
|
| 固有(基底)関数 |
φk(r) |
φ(x,k),δ(r'−r) |
| 演算子 |
T=ΣΣ|aj><aj|T|ak><ak| |
| T= |
 |
d rdr'|r><r|T|r'><r'| |
|
| 状態の重なり |
<φ|ψ>=Σ<φ|aj><aj|ψ> |
| <φ|ψ>= |
 |
dr<φ|r><r|ψ> |
|
| 観測値 |
<aj|A|ak>=akδjk |
<r|r|r'>=r'δ(r'-r) |
いくつか丁寧に書くと,
| x|x'>= |
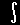 |
x|x><x|x'>dx ・・・・[*1] |
| = |
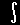 |
x|x><x|x'>dx |
| = |
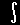 |
x|x>δ(x'-x)dx |
のような計算ができます。座標表示(波動関数)への対応は,
| (x-)座標表示 |
⇔ |
δ関数 |
| <x|x'>= |
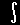 |
<<x|x"><x"|x'>dx" [*2] |
|
| f(x')= |
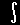 |
f(x")δ(x"-x')dx" |
|
| <x|x'> |
f(x') |
| <x|x"> |
f(x") |
| <x"|x'> |
δ(x"-x') |
位置固有ケット|x'>の座標表示<x|x'>はδ関数δ(x-x')でもあるので,[*2]はデルタ関数の公式,
| δ(a−b)= |
 |
δ(x−a)δ(x−b)dx |
|
|
に対応しています。
一般的な連続固有関数と連続固有値の考え方
連続固有値kに対応する連続固有関数を
φn(x) [離散的] ⇒ φ(x,k) [連続的]
とおきます。(L2空間の)状態関数ψ(x)はこの固有関数を用いて,
| ψ(x)= |
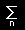 |
cnφn(x) [離散的] ⇒ ψ(x)= |
 |
c(k)φ(x,k)dk [連続的] |
と展開できることとします。このとき,波動関数に確率的な意味を持たせるために,
 |
ψ*(x)ψ(x)dx=1 ・・・[*] |
また,展開係数については,
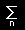 |
cn*cn=1 [離散的] ⇒ |
|
 |
c*(k)c(k)dk=1 [連続的] ・・・[**] |
であることを要請します。そこで,状態関数を[*]に代入すると,
 |
 |
 |
c*(k)φ*(x,k)dk |
 |
c(k')φ(x,k')dk' |
 |
dx=1 |
積分順序を交換すると,(フビニの定理)
 |
 |
c*(k)c(k') |
 |
 |
φ*(x,k)φ(x,k')dx |
 |
dk'dk=1 |
ここで,xに関する積分の部分を
| δ(k,k')= |
 |
φ*(x,k)φ(x,k')dx ・・・[***] |
|
とおけば,
 |
 |
c*(k)c(k')δ(k,k') dk'dk=1 |
という関係が得られます。さらに,この式を[**]と比較すれば,
 |
c(k')δ(k,k') dk'=c(k) |
でなければ辻褄が合わないこともわかります。この式を見ると,δ(k,k')はk'=kのときだけc(k')に作用し,c(k)を取り出すような働きがあることがわかります。そこで,δ(k,k')はk'=kのときだけ意味をもち,他のところではゼロの値しか持たないとしてもよいでしょう。すると,上の式は次のように小さな正数εを用いて積分範囲を限定しても成り立つはずです。
| c(k)= |
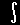 |
k+ε |
c(k')δ(k,k') dk' |
|
| k-ε |
ここで,c(k')が連続関数であるならば,この積分範囲でc(k')≒c(k)として積分の外に出すことができ,
| c(k)=c(k) |
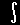 |
k+ε |
δ(k,k') dk' |
|
| k-ε |
すなわち,
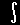 |
k+ε |
δ(k,k') dk'=1 |
|
| k-ε |
でなければいけません。ここで,δ(k,k')はk=k'であるかどうかだけが重要なのでδ(k−k')と書くことにします。するとδ(k−k')は,k=k'
で∞,k≠k' で 0 の値をとり,(-∞,+∞)において積分すると1となる(超)関数であることがわかります。数学的に厳密な超関数についてはルベーグ積分(の中のヒルベルト空間論)のところで説明します。[#])
| δ(k−k') = |
 |
∞ (k=k') |
| 0 (k≠k') |
|
これがディラックの考え出したデルタ関数です。
さらに,具体的な連続固有関数として平面波
| φ(x,k)= |
1 |
exp(i kx) |
|
|
|
 |
2π |
|
|
を考えましょう。この関数を用いると(逆)フーリエ変換(と呼ばれる積分)によって,任意の(L2)関数を展開することができますが,この関数場合,[***]は次のように書かれることが確かめられます。
 |
φ*(x,k)φ(x,k')dx= |
1 |
 |
exp(i (k−k')x)dx =δ(k−k') [#] |
|
| 2π |
|
離散的な場合と違って,連続固有関数の正規直交性とは,k=k' のときに1ではなく,∞となること。
(違和感を感じる人が多いと思うが,δ関数は超関数で,積分記号の中でだけ意味を持つことからこれでもおかしくない!)
| 平面波φ(x,k)を状態関数の展開式: ψ(x)= |
 |
c(k)φ(x,k)dk に代入すると, |
| ψ(x)= |
1 |
 |
c(k)exp(i kx)dk |
|
|
|
 |
2π |
|
| この両辺(変数x→x’と書き換え)に |
1 |
exp(-i k'x')をかけ,x'について(-∞,∞)で積分すると, |
|
|
|
 |
2π |
|
| 1 |
 |
ψ(x')exp(-i k'x')dx'= |
  |
c(k) |
1 |
 |
exp{i (k−k')x'}dkdx' |
|
|
|
|
 |
2π |
|
2π |
| = |
 |
c(k)δ(k−k')dk |
=c(k') ( ≡Ψ(k') )
上の計算では積分順序を交換し,また,公式
| 1 |
 |
exp{i (k−k')x'}dx'=δ(k−k') |
|
| 2π |
を用いました[#]。
ここまでの関係を,c(k) ⇒ Ψ(k) と記号を改めてまとめると,
| ψ(x)= |
1 |
 |
Ψ(k)exp(i kx)dk |
|
|
|
 |
2π |
|
| Ψ(k)= |
1 |
 |
ψ(x)exp(-i kx)dx |
|
|
|
 |
2π |
|
|
これはフーリエ変換と逆フーリエ変換の関係と同じです。さらに,
| ψ(x)= |
1 |
 |
c(k)exp(i kx)dk |
|
|
|
 |
2π |
|
| = |
1 |
 |
 |
1 |
 |
ψ(x')exp(-i kx')dx' |
 |
exp(i kx)dk |
|
|
|
|
 |
2π |
|
|
|
 |
2π |
|
| = |
1 |
 |
 |
|
ψ(x')exp{-i k(x'−x)}dx'dk [フーリエ積分公式] |
|
| 2π |
これは状態関数ψ(x)の基底関数による展開式を表しています。以上の議論で,k→p/h とすれば,位置xと運動量pとがフーリエ変換で関係付けられていることがわかります。
3.運動量演算子
位置演算子と対になるもう一つの連続基底して運動量演算子があります。
定義:
[1] 位置演算子と同様に,自由粒子の運動量は任意の実数値をとれることから,運動量固有ケットと呼ばれる|p>をこの空間の基底に選ぶことにすれば,運動量演算子p,運動量固有値pとする固有方程式,
と定義することができます。また,
<p'|p>=δ(p'−p)
| |ψ>= |
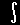 |
dp|p><p|ψ> |
|
とできることも位置固有ケットの場合と同じです。
[2] つまり,状態ケットは基底{|p'>}でも{|r'>}でもどちらでも表せるわけです。では,これらの基底や演算子との関係はどうなっているのでしょうか。この2つの基底はまったく独立した存在でないことは,互いに等速運動する座標系はすべて等価なことから推測できます(相対性原理[#])。その表現方法はいくつかあります。形式的には次のような演算子の正準交換関係:
↑古典力学では [rj,pk]=δjk 詳細は[#]
を要請する(記号法については末尾参照[#])と古典力学との対応関係が明白ですっきりします。しかし,具体的に計算を進めることを考えれば次式を原理的要請とすることもでき,実用的です。
運動量演算子の定義 [原理的要請]
運動量の任意のケット|ψ>に対しての位置固有ケットによる展開は,
| p|ψ>= |
 |
dr'|r'> |
 |
−ih |
∂ |
<r'|ψ> |
 |
|
| ∂r' |
|
この定義は量子力学の原理としての交換関係,[qj,pk]=qjpk−pkqj=ihδjk
この定義の左辺より<r|をかけるとδ(r−r')=<r|r'>の性質[#]より,
| <r|p|ψ>= |
 |
δ(r−r') |
 |
−ih |
∂ |
<r'|ψ> |
 |
dr' |
|
| ∂r' |
<r| p|ψ>=−ih∇<r|ψ> ← 3次元
および,|ψ>を|r'>とおいて,pの行列要素(r-表示):
<r|p|r'>≡−ih |
∂ |
・δ(r−r') |
|
| ∂r |
という重要な式が導かれます。これらを用いて,<r|[rp−pr]|ψ>を計算すると,[r,p]=ih が確認できます。⇒[#]
つまり,こうなるように運動量演算子に原理的要請を課したということです。
位置演算子と運動量演算子に関する重要な関係式の対比してまとめました。
|
位置 |
運動量 |
| 固有方程式(1次元) |
r|r>=r|r> |
p|p>=p|p> |
| 固有方程式(成分) |
rk|rk>=rk|rk> |
pk|pk>=pk|pk> |
| 固有方程式(3次元) |
r|r>=r|r> |
p|p>=p|p> |
| 直交性 |
<r'|r>=δ(r'−r) |
<p'|p>=δ(p'−p) |
| 演算子成分 |
<r'|r|r>=rδ(r'−r) |
<p'|p|p>=pδ(p'−p) |
| 規格化 |
| 1= |
 |
d r<ψ|r><r|ψ> |
|
| 1= |
 |
d p<ψ|p><p|ψ> |
|
| 状態関数の展開 |
| |ψ>= |
 |
d r|r><r|ψ> |
|
| |ψ>= |
 |
d p|p><p|ψ> |
|
| 恒等演算子 |
| I = |
 |
d r|r><r| |
|
| I = |
 |
dp|p><p| |
|
| 波動関数の表示 |
ψ(r)=<r|ψ> |
ψ(p)=<p|ψ> |
|
ψ*(r)=<ψ|r> |
ψ*(p)=<ψ|p> |
pn,rnの行列要素
(形式的) |
<r|pn|ψ>≡(−ih)n |
∂n |
<r|ψ> |
|
| ∂rn |
|
<p|rn|ψ>≡(ih)n |
∂n |
・<p|ψ> |
|
| ∂pn |
|
p,rの行列要素
(形式的) |
<r|p|r'>≡(−ih) |
∂ |
・δ(r−r') |
|
| ∂r |
|
<p|r|p'>≡ih |
∂ |
・δ(p−p') |
|
| ∂p |
|
|
|
|
| 変換関数 |
<r|p>=N・exp[ipr/h] |
<p|r>=N・exp[-ipr/h] |
|
|
|
| 波動関数の変換 |
| <r|ψ>= |
 |
d p<r|p><p|ψ> |
|
| <p|ψ>= |
 |
d r<p|r><r|ψ> |
|
| 交換関係 |
[ r,pn]=n・ihpn-1 |
[ p,rn]=−n・ihrn-1 |
* N=1/[2πh]1/2
このHPで使われる位置,運動量に関係した記号をまとめておきます。
| 一般的記号 |
具体的記号 |
| 1次元成分 |
3次元の記号 |
| 位置演算子 |
x,y,z |
r |
| 位置固有値 |
x,y,z |
r |
| 位置固有ケット |
|x>,|y>,|z> |
|r> |
| 運動量演算子 |
px,py,pz |
p |
| 運動量固有値 |
px,py,pz |
p |
| 運動量固有ケット |
|px>,|py>,|pz> |
|p> |
成分kを
強調したいとき |
rk,rk,|rk> ; pk,pk,|pk> |
[補1] [r,p]=rp−pr=ih の証明
任意の|ψ>に対して,
<r|(rp−pr)|ψ>=<r|ih|ψ>=ih<r|ψ>
を示したらよいでしょう。まず,
<r|rp|ψ>={ <r|r}・p|ψ>
=r <r|p|ψ>
=−r・ih |
∂ |
<r|ψ> ・・・・(1) |
|
| ∂r |
一方,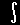 d r''|r''><r''|を挿入して,
d r''|r''><r''|を挿入して,
| <r|pr|ψ>= |
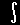 |
d r''<r|p|r''><r''|r|ψ> |
| = |
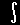 |
dr''{−ih |
∂ |
・δ(r−r'')r''|<r''|ψ>} |
|
| ∂r |
=−ih |
<r|ψ>−r・ih |
∂ |
<r|ψ> ・・・・(2) |
|
| ∂r |
これら2式の差(1)−(2)をとれば,証明する式になります。
[目次へ]
SUSTAINABLE TOKIWADAIGAK SINCE 2002
自由粒子
真空中をただ一つの粒子が等速直線運動するという自由粒子の場合,シュレーディンガー方程式は
ただし,
となります。このハミルトニアンの固有関数は
| ψ(r,t)=φ(r)exp[−iωt]=− |
1 |
exp[i k・r−iωt] |
|
| (2π)3/2 |
ここで, k=p/h , ωh=E=p2/(2m)=(h2k2)/(2m)
これを平面波といいます。規格化条件,
|
 |
ψ*k'ψkd r3=δ(k'−k) |
位置と運動量の交換関係
[rj,pjn]=nihpjn-1
[pj,rjn]=nihrjn-1
![]() d r''|r''><r''|を挿入して,
d r''|r''><r''|を挿入して,