 |
111 1電子-水素様原子 |
|
| f-denshi.com 更新日： |
|
| サイト検索 |
|
このページはコンパクトに結果だけをまとめるにとどめました。
１．シュレーディンガー方程式の解
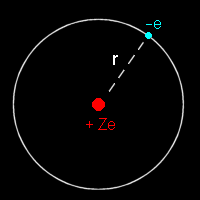
定常状態にある水素様原子（＝中心にZ価の正電荷のまわりにただ１つの電子が束縛されている系）（右図）の1電子シュレーディンガー方程式とポテンシャルエネルギーは，
 |
− |
h2 |
|
∂2 |
＋ |
∂2 |
＋ |
∂2 |
 |
＋V（rx,y,z） |
|
ψ(x,y,z)＝εψ(x,y,z) |
|
|
|
|
| 2m |
∂x2 |
∂y2 |
∂z2 |
| V（r ） ＝− |
Z e2 |
( ＝ |
h2 |
|
Z |
|
|
|
| 4πε0 r |
m |
r |
で与えられます。ここで，電子の位置ベクトル r の大きさを，r ＝｜r｜としています。
これを球座標 [#] に変換すると次のようになります。
| − |
h2 |
|
∂2 |
＋ |
2 |
･ |
∂ |
＋ |
1 |
Λ＋V（r） |
|
Φ（r，θ，φ）＝εΦ（r，θ，φ） ････ [*] |
|
|
|
|
|
| 2m |
∂r2 |
r |
∂r |
r2 |
|
ただし，
| Λ ＝ |
1 |
･ |
∂ |
|
sinθ |
∂ |
|
＋ |
1 |
･ |
∂2 |
|
|
|
|
|
| sinθ |
∂θ |
∂θ |
sin2θ |
∂φ2 |
（角運動量演算子：L2 ＝ −h2Λ ）
これは， Φ（r，θ，φ） ＝ R（r）･Y（θ，φ） とおくと，
| − |
h2 |
|
∂2R（r） |
＋ |
2 |
･ |
∂R（r） |
＋ |
λ |
R（r） |
|
＋V（r）R（r） ＝ εR（r） ･････ (1) |
|
|
|
|
|
| 2m |
∂r2 |
r |
∂r |
r2 |
ΛY（θ，φ）＋λY（θ，φ） ＝ 0
･････ (2) |
という２つの方程式に分解されます[#]。 これらの解，
R（r） ＝ Rnl（r） は動径関数，
Y（θ，φ）＝ Ylm（θ，φ） は球面調和関数
n ＝ 1，2，3，･･･，； ｌ ＝ 0，1，2，･･･，n−1； m ＝ -l，-l +1，･･･，0，･･･l -1，l
と呼ばれます。これらの記号を使えば，
水素様原子
固有関数： Φ（r，θ，φ） ＝ Rnl（r）･Ylm（θ，φ）
| 固有値： εn ＝ − |
mZ2e4 |
＝− |
e2 |
・ |
Z2 |
|
|
|
32π2ε02h2n2 |
4πε0 a0 |
2n2 |
| ＝ − |
|
|
|
|
|
|
ここで，
| a0 ＝ |
4πε0h2 |
＝ 0.0529 nm ［ボーア半径］ |
|
| m e2 |
| Ry ＝ − |
e2 |
＝ 13.6 eV ［ ？ ］ |
|
| 8πε0a0 |
cf.
| R∞ ＝｜Ry/hc｜＝ |
e2 |
|
＝ |
me4 |
＝1.097×107 m-1 ［リュードベリ定数］ |
|
|
| 8πε0a0 |
8πε02h3c |
２．動径関数の具体的な形
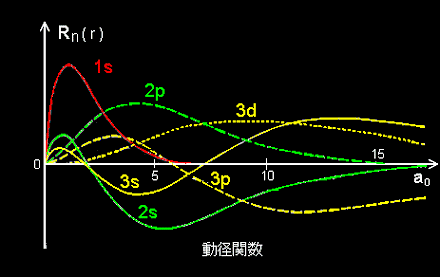
| Rnl(ρ)＝− |
|
|
 |
|
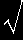2Z |
|
3 |
|
(n-l-1)! |
|
|
|
| na0 |
2n{ (n+l)! }3 |
|
|
e-ρ/2ρl Ln+l-12l＋1(ρ) |
| ρ＝ |
|
2Z |
|
r |
|
| na0 |
ラゲール陪関数 Lnm は こちら ⇒ [#]
２．角運動量
角運動量演算子：L2 ＝ −h2Λ
L2 Ylm（θ，φ）＝l （l ＋1）h2Ylm（θ，φ）
球面調和関数 Ylm ⇒ こちら
３．電子スピン量子数
４．スピン軌道相互作用
| Z が小さい |
Z が大きい |
| S-L 相互作用は小さく無視できる |
S-L 相互作用は大きく無視できない |
| s と ｌ はそれぞれ個別に保存される。 |
全角運動量 J （＝ｌ＋s ） だけが保存される。 |
スピン軌道相互作用の計算は ⇒ こちら
