| 305 逆格子空間 | |
| f-denshi.com 更新日:05/02/17 | |
| サイト検索 | |
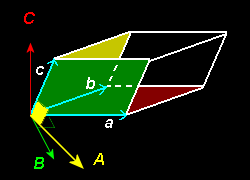 [1] 3次元ベクトル空間は,任意の1次独立な3つのベクトル(=基底という)を用いて取り扱うことができます。結晶構造を取り扱うときにもっとも自然で重要な基底は,これまでの説明に用いた3つの基本並進ベクトル,{a,b,c } を採用することです。
[1] 3次元ベクトル空間は,任意の1次独立な3つのベクトル(=基底という)を用いて取り扱うことができます。結晶構造を取り扱うときにもっとも自然で重要な基底は,これまでの説明に用いた3つの基本並進ベクトル,{a,b,c } を採用することです。
もう一つの重要な基底ベクトルは,これから述べる逆格子ベクトルです。
ベクトル空間の3つの基底として,次のような性質をもつベクトルA,B,C を逆格子ベクトルといいます。すなわち,
A はb,c に垂直 : A ・b = A ・c = 0
B はc,a に垂直 : B ・c = B ・a = 0
C はa,b に垂直 : C ・a = C ・b = 0・・・・・[*]
であって,A,B,C の大きさが,
A ・a = 2π
B ・b = 2π
C ・c = 2π・・・・・[**]
となるように定めたベクトルです。これは数学的には基底:{a,b,c }の相反基底:{A,B,C }とよばれます[#]。
また,3次元ベクトル空間の基底として, {a,b,c }を選んだときを実空間,(A,B,C )を選んだときを逆格子空間と呼びます。)
具体的な逆格子ベクトルは基本並進ベクトルの外積を用いて,
A =2π b×c ,B =2π c×a ,C =2π a×b [abc] [abc] [abc]
を計算することで得られます。ここで,[abc]=a ・(b×c ) はスカラー三重積 [#] です。
|
重要な関係式
(2) G = hA + kB + lC は( h k l )面に垂直である。
|
証明
(1) ベクトル解析の相反基底の公式 3 (2)[#]においては,ベクトルと相反基底との関係が,A ・a = 1 ですが,それをここでの定義,A ・a = 2π に変える必要があります。
(2) ( h k l ) 面(右下図の緑色の三角形を含む面)内の任意の異なる2点を示すベクトルは,代数・幾何学の公式から
r1 =p1 a +q1 b +r1 c , r2 =p2 a +q2 b +r2 c h k l h k l ただし, p1+q1+r1 = 1, および, p2+q2+r2 = 1
と表すことができます。 この面内の2点を結ぶベクトル,( つまり,( h k l )面内にあるベクトル )r = r1 −r2 と,G = hA + kB + lCとの内積は,[*] と[**] を用いて,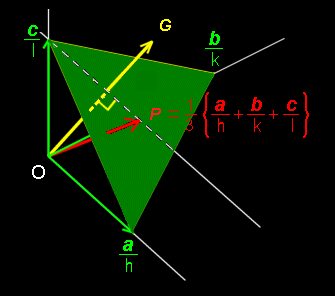
G ・r =(hA+kB +lC)・ p1−p2 a+ q1−q2 b + r1−r2 c h k l =(p1−p2)(A・a )+(q1−q2)(B・b )+(r1−r2)(C・c )
= 2π{( p1+q1+r1 )−(p2+q2+r2)}
= 2π{ 1 − 1 }
= 0
と計算できます。よって,G は r に垂直です。
(3) 原点からもっとも近い(隣の)( h k l )平面上の点,
P = 1 a + b + c 3 h k l
を示すベクトルを考え,その ( h k l )平面に垂直な単位ベクトル G / | G | への射影を求めればよい。すなわち,
d( h k l ) = P ・ G = 1 a ・A +b ・B +c ・C | G | 3 | G |
= 1 (2π+2π+2π) = 2π 3 | G | | G |
面の多重度
| 結晶系 | hkl | hhl | hk0 | 0kl | h0l | hh0 | hhh | h00 | 0k0 | 00l | ||
| 三斜晶系 | 2 | |||||||||||
| 単斜晶系 | 4 | 2 | 2 | |||||||||
| 斜方晶系 | 8 | 4 | 4 | 4 | 2 | 2 | 2 | |||||
| 正方晶系 | 16 | 8 | 8 | 8 | 4 | 4 | 2 | |||||
| 六方晶系 三方晶系 |
24 | 12 | 12 | 12 | 6 | 6 | 2 | |||||
| 立方晶系 | 48 | 24 | 24 | 12 | 8 | 6 | ||||||
 |
 |
 |
 |