 |
801 スピン演算子 |
| f-denshi.com 更新日: |
| サイト検索 |
1.スピン1/2の系
[1] 静磁場中におかれた電子の磁化の測定から,電子はスピンと呼ばれる磁気モーメントに比例する角運動量をもつことが知られています。スピンのある方向成分,例えば,z成分を測定すると,絶対値が等しく符号が反対の2とおりの値だけをとります。
(このとき,同時にx 成分,y 成分を測定によって定められるわけではありません。)
量子力学の原理的要請 [#]に基づいた形式で記述するならば,エルミート演算子 Sz ,2つのスピン状態に対応する固有ケット |Sz ,+>,|Sz ,−> が存在して,これらは次のような固有方程式:
Sz|Sz ,+>= (h/2)|Sz ,+>
Sz|Sz ,−>=−(h/2)|Sz ,−> |
・・・・・ (1) |
を満しなければなりません。ここで,固有値: s+=(h/2),s-=−(h/2) をスピン角運動量と呼びます。
この2つの固有ケット {|Sz ,+>,|Sz ,−>} を,
{|+>,|−>} ← 一般論で, {|a1>,|a2>,・・・,|an>} と書いたもの[#]に対応
と書いてスピンを記述するユニタリ空間の正規直交基底に用いましょう。つまり,このケットは,
<+|+>=<−|−>= 1 [ 大きさが1 ]
<+|−>=<−|+>= 0 [ 直交性]
を満足しなければいけません。 このとき,この空間内の任意のスピン状態を表すケットは係数
c+, c- を用いて,
|γ>=c+|+>+c-|−>
と線形結合で表すことができます。 また,|γ> は規格化条件から, c+, c- は,
<γ|γ>=c*+c++c*-c-=1
を満たす必要があります。
(スピン空間は複素数を要素とする2次元空間なので,実質的には4次元空間を考えていることに注意しましょう。)
[2] 基底{|+>,|−>}で,固有ケット|Sz ,+>,|Sz ,−> の行列表現 [#]は,
| |Sz ,+>=|+>= |
 |
<+|Sz ,+> |
 |
= |
 |
1 |
 |
| <−|Sz ,+> |
0 |
| |Sz ,−>=|−>= |
 |
<+|Sz ,−> |
 |
= |
 |
0 |
 |
| <−|Sz ,−> |
1 |
となります。 また,演算子 Sz の行列表現は,(1)を用いて,
<+|Sz|+>=<+|(h/2)|+>=(h/2)<+|+>=(h/2)
のように計算すれば,
| Sz= |
 |
<+|Sz|+><+|Sz|−> |
 |
= |
 |
(h/2) |
0 |
 |
| <−|Sz|+><−|Sz|−> |
0 |
−(h/2) |
となります。
[3] 射影演算子,恒等演算子 [#] はそれぞれ,
| Λ+=|+><+|= |
 |
1 |
 |
( 1 0 )= |
 |
1 0 |
 |
| 0 |
0 0 |
| Λ-=|−><−|= |
 |
0 |
 |
( 0 1 )= |
 |
0 0 |
 |
| 1 |
0 1 |
| I =|+><+| + |−><−|= |
 |
1 0 |
 |
| 0 1 |
これを用いて
| Sz= |
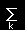 |
skΛk |
=(h/2)|+><+|+(−h/2)|−><−| |
なる関係 [#]も容易に確かめられます。
[4] z方向に垂直な x,y の2つの方向について考えた Sx,Sy も それぞれ z方向の場合と同様な記述ができるはずです。そのときの基底としては
Sx,Sy の固有ケットを基底にそれぞれ用いれば,単に記号を,z→x, z→y と置き換えて,
Sxの固有ケットで,
Sx|Sx ,+> (h/2)|Sx ,+>
Sx|Sx ,−>=−(h/2)|Sx ,−> |
: |
Sy|Sy ,+>= (h/2)|Sy ,+>
Sy|Sy ,−>=−(h/2)|Sy ,−> |
とすればすみます。 しかし,2次元の系を記述するのに必要な基底は2つあればよく,先の
Sz の固有ケットで用は足りているはずです。そこで,Sz の固有ケットを用いて,
|Sx ,+>=c+|+>+c-|−> ; c*+c++c*-c- = 1
と表すことにしましょう。 ここでは結果だけかくと,[脚注]
| |Sx ,+>≡ |
1 |
(|+>+|−>) ; |
|Sx ,−>≡ |
1 |
(|+>−|−>) |
|
|
|
|
 |
2 |
|
|
|
 |
2 |
|
| |Sy ,+>≡ |
1 |
(|+>+i|−>) ; |
|Sy ,−>≡ |
1 |
(|+>−i|−>) |
|
|
|
|
 |
2 |
|
|
|
 |
2 |
|
となります。これらのケットの行列表現は,
| |Sy ,−>= |
 |
<+|Sy ,−> |
 |
| <−|Sy ,−> |
| = |
1 |
 |
<+|{|+>−i|−>} |
 |
= |
1 |
 |
1 |
 |
|
|
|
|
|
|
 |
2 |
|
<−|{|+>−i|−>} |
|
|
 |
2 |
|
-i |
| <Sy,−|= |
1 |
( 1 i ) ← 虚数の符号反転に注意 |
|
|
|
 |
2 |
|
などと計算すればよく,まとめると次のようになります。
| ケット |
基底 { |+> ,|−> }での表示 |
| |Sx ,+>= |
| 1 |
(|+>+|−>) |
|
|
|
 |
2 |
|
|
|
| |Sx ,−>= |
| 1 |
(|+>−|−>) |
|
|
|
 |
2 |
|
|
|
| |Sy ,+>= |
| 1 |
(|+>+i|−>) |
|
|
|
 |
2 |
|
|
|
| |Sy ,−>= |
| 1 |
(|+>−i|−>) |
|
|
|
 |
2 |
|
|
|
| |Sz ,+> = |
|+> |
 |
1 |
 |
| 0 |
|
| |Sz ,−> = |
|−> |
 |
0 |
 |
| 1 |
|
[5] 一方,演算子については,例えば, Sy は,
(その1)[#]
Sy =ΣsyΛy
=(h/2)|Sy ,+><Sy,+| + (−h/2)|Sy ,−><Sy,−|
=(h/2)(1/2)(|+>+i|−>)(<+|−i<−|)+(−h/2)(1/2)(|+>−i|−>)(<+|+i<−|)
=(ih/2)[ −|+><−|+|−><+| ]
これを用いて次式の成分を計算すれば,
| Sy = |
 |
<+|Sy|+> <+|Sy|−> |
 |
= |
 |
0 −i(h/2) |
 |
| <−|Sy|+> <−|Sy|−> |
i(h/2) 0 |
例えば,1行1列目は,<+|(ih/2)[ −|+><−|+|−><+| ]|+>=0
(その2) |Sy ,+> と <Sy,+| のベクトル成分で表してから,
Sy =(h/2)|Sy ,+><Sy,+| + (−h/2)|Sy ,−><Sy,−|
=(h/2) |
1 |
 |
1 |
 |
・ |
1 |
(1 −i )−(h/2) |
1 |
 |
1 |
 |
・ |
1 |
(1 i ) |
|
|
|
|
|
|
|
|
 |
2 |
|
i |
|
|
 |
2 |
|
|
|
 |
2 |
|
-i |
|
|
 |
2 |
|
= (h/2)(1/2) |
 |
1 −i |
 |
−(h/2)(1/2) |
 |
1 i |
 |
| i 1 |
−i 1 |
=
|
 |
0 |
−i(h/2) |
 |
i(h/2) |
0 |
と求めることができます。
[6] スピン演算子のケットでの表現と行列表現をまとめると次のようになります。
| スピン |
ケット |
行列 |
| Sz ≡ |
|
|
|
 |
1 0 |
 |
= |
|
σz |
| 0 -1 |
|
| Sx ≡ |
|
|
|
 |
0 1 |
 |
= |
|
σx |
| 1 0 |
|
| Sy ≡ |
|
|
|
 |
0 -i |
 |
= |
|
σy |
| i 0 |
|
ここで上の各 Sk をh/2 を除して得られる3つの行列 σk ;( k = x,y,z ) をパウリ行列といいます。
パウリ行列のもつ重要な性質を列挙しておくと,
(1) trσk = 0 [トレース]
(2) |σk| = -1 [擬回転]
(3) [σi ,σj ]= 2iεijkσk [交換関係]
(4) {σi ,σj }= 2δij I [反交換関係]
[7] さて,エルミート演算子ではありませんが,昇降演算子と呼ばれるたいへん重要な演算子の定義しておきましょう。
S+ ≡ h|+><−|
S- ≡ h|−><+|
これは,
S+|+>= h|+><−|+> = 0 ; S+|−>= h|+><−|−> = h|+>
S-|+>= h|−><+|+> = h|−> ; S+|−>= h|−><+|−> = 0
のように働くので,S+,S- はそれぞれスピンを h だけ増やしたり,減らしたりする演算子であることがわかります。
(調和振動子の消滅演算子・生成演算子のスピン-version です。)
ここで,
なる関係にあることも先ほども求めた行列表現を用いて計算すればわかります。
[8] 一方,スピンの大きさの2乗を,
| S2≡Sx2+Sy2+Sz2= 3 |
 |
h |
 |
2 |
|
|
| 2 |
|
|
 |
1 0 |
 |
| 0 1 |
のように定義素ましょう。以上まとめて,
スピン
演算子 |
ケット |
行列 |
| S2≡ |
Sx2+Sy2+Sz2 |
|
|
 |
1 0 |
 |
| 0 1 |
|
| S+≡ |
h|+><−| |
h |
 |
0 1 |
 |
| 0 0 |
|
| S-≡ |
h|−><+| |
h |
 |
0 0 |
 |
| 1 0 |
|
S+† = S- ,および, S-† = S+
[9] これらの行列表現を使って計算すると次の交換関係が確かめられます。
交換関係
|
[ Sz ,Sx ]=SzSx−SxSz=ihSy
[ Sx ,Sy ]=SxSy−SySx=ihSz
[ Sy ,Sz ]=SySz−SzSy= ihSx
|
[ S2 ,Sj ]=0 ⇔ S2 ,Sj には同時固有ケットが存在する ( j = x,y,z )。
|
すると,
S2 = Sx2 + Sy2 + Sz2
= (Sx+i Sy)(Sx−i Sy)+i (SxSy−SySx)+ Sz2
= S+S- + i (ihSz)+Sz2
=S+S- − hSz + Sz2
同様に,
S2 = (Sx−i Sy)(Sx+i Sy)−i (SxSy−SySx)+ Sz2
=S-S+ + hSz + Sz2
これらから,有用な公式:
S2−Sz2 =(1/2)(S+S- +S-S+)
S+S- = S2 + hSz − Sz2
S-S+ = S2 − hSz − Sz2 |
[10] 最後に行列を用いた簡単な計算から反交換関係が次のように成り立つことを喚起してスピン入門はお終いです。
|
反交換関係
{ Si Sj } = SiSj+SjSi = (h/2)2δij
|
[目次へ]
さらにスピン,2準位系について学びたい方は以下のPDFを参考にしてください。
統計力学 I 目次



(脚注)
回転対称性の考察による,|Sx,±>,|Sy,±> の決め方
(1) 回転に対する対称性から,
|<±|Sx ,+>|2=|<±|Sx ,−>|2 = 1/2 ・・・・・・・(1)
|<±|Sy ,+>|2=|<±|Sy ,−>|2 = 1/2 ・・・・・・・(2)
|<Sy ,±|Sx ,+>|2=|<Sy ,±|Sx ,−>|2 = 1/2 ・・・・・・・(3)
<Sx ,−|Sx ,+>= <Sy ,−|Sy ,+>=0 ・・・・・・・(4)
を利用する。
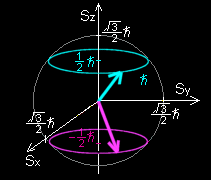 |
| S2の固有値は, |
3h2 |
なので,スピンの大きさは |
|
|
 |
3 |
|
h |
|
|
| 4 |
2 |
と考えることができる。一方,z方向のスピンの測定値が,
±(1/2)h であるとき,x,y方向のスピンは同時には定まらない。
この様子は,左のようなベクトルの模式図で表される。
|
任意の2行2列の行列Aは,単位行列 I とパウリ行列の線形結合で表すことができます。すなわち,
A = a0 I + a1σx + a2σy + a3σz
これは,
| A = |
 |
a +i b c +i d |
 |
= a0 |
 |
1 0 |
 |
+ a1 |
 |
1 0 |
 |
+ a2 |
 |
0 1 |
 |
+ a3 |
 |
0 -i |
 |
| e +i f g +i h |
0 1 |
0 -1 |
1 0 |
i 0 |
において,
