ファラデーの法則とフレミング右手の法則
| 12 電磁誘導: ファラデーの法則とフレミング右手の法則 |
||
| f-denshi.com [目次へ] 最終更新日:09/05/8 ファラデーの法則の説明を訂正しました。 | ||
| サイト検索 | ||
これまでは運動する電荷(=電流)と静止した磁荷との(=静磁場を介しての)相互作用についてについて考えてきましたが,運動の相対性からそこに働く力は運動する磁荷と静止した電荷との(電場を介しての)相互作用とみなすことも可能です。
すなわち,磁荷の運動によって電場が発生し,その結果,電流が流れるという法則
(=ファラデーの電磁誘導の法則) が予言可能なのです。
ある時刻において,右下図のような位置・速度関係にある電荷 Q と磁荷 Qm を次のような2つの座標系で考察します。
[1] 一つは座標系ΣMでは,「磁荷Qmが原点に静止しており,-rの位置に電荷Qが等速度(-v )で z 方向(上方)へ移動する」ことが観測されることとします。このとき,静止している磁荷Qmが運動する電荷Qの位置-rに作る静磁場は磁荷のクーロンの法則[#]により,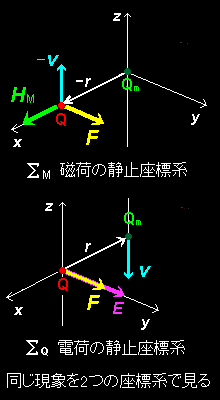
H M= Qm(-r) 4πμ0 r3
となります。この静磁場中をz方向に運動する電荷Qが受けるローレンツ力[#]は方向も考えて,
F =Q(-v )×(μ0H M)= μ0QmQ(-v )×(-r) 4πμ0r3
と表せます。
[3] 同じ現象を,「電荷Qが原点に静止しており,磁荷が位置r において下方へ速度v で動いているように見える座標系ΣQで観測することもできます。この座標系では,
「磁荷Qmの運動によって,静止している電荷Qに働く力F が誘起される。」
ように見えます。すなわち,”磁荷の運動によって電場E が発生する”という法則が必然的に導かれます。これを電磁誘導の法則といいます。この発生した電場が電荷Qに及ぼす力F の大きさ,方向は先の座標系で求めたものと当然,同一でなければなりません。それは今,考えてる座標系ΣQでは磁荷の速度の符号を正にとり,
F =Q Qmv ×r 4πr3
と書き直す方がよいでしょう。 これと電場を用いた電荷のクーロンの法則,F =QE と比較すると,
この式では,v が-z方向を向いていることは忘れ去ってしまってもよい。
E = Qmv ×r ( = −v ×μ0HM ) :v は磁荷の速度 4πr3
なる電場が座標系ΣQの原点に発生しているとみなせることがわかります。つまり,電荷が静止して見える座標系ΣQでは,
「磁荷が運動 (=磁場が変動) することで周りに電場が誘起される。」
という法則を主張できるのです。
[4] さて,磁荷の運動によって電場が生じるならば,運動する磁荷のそばに導体でできた閉回路が存在すると電流が流れる可能性があります。ここではループ状に閉じた閉回路にどのような電流が流れるのか考察しましょう。可能性といったのは,電場が存在するからといって無条件にループ電流が流れるわけではないからです。閉回路の各位置にできる電場の閉回路に沿った方向の成分が閉回路全体ではキャンセルし合い,電流がゼロとなる可能性(=正確には導体内部の電場がゼロとなるような分極の形成)もあるからです。
真偽の程は具体的に円形の導電体閉回路に沿った次のような電場の線積分を計算して見る必要があります。もし閉回路に電流が流れるならば,この積分値は閉回路の一方向に沿って電流を流す起電力
Vf になります。
その計算は,先程求めた磁荷の運動によってできる電場E を用いて,
Vf = E ・ds = Qm(v ×r )・ds [=起電力] 4πr3
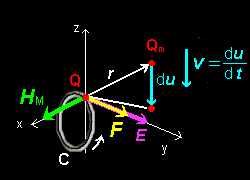 という線積分を行えばよいでしょう。ここで,閉回路にそった微分線要素を ds,閉回路の一点から磁荷 Qm を指す位置ベクトルを r,磁荷 Qm の移動速度を v = du/dt として,閉回路のループCの向きを Qmの作る磁場 HM の方向と同じ (内積 HM・dS ≧ 0 ) にとっています。(右図)
という線積分を行えばよいでしょう。ここで,閉回路にそった微分線要素を ds,閉回路の一点から磁荷 Qm を指す位置ベクトルを r,磁荷 Qm の移動速度を v = du/dt として,閉回路のループCの向きを Qmの作る磁場 HM の方向と同じ (内積 HM・dS ≧ 0 ) にとっています。(右図)
v → du/dt の置き換えとスカラー3重積の公式[#]を用いて,
E ・ds = Qm(r ×ds )・v 4πr3
= Qm du ・ (r ×ds) 4πdt r3
↓ 立体角dΩの定義 [#] を用いて,(この周辺の理解には立体角の知識が必須です)
E ・ds =−(Qm/4π) dΩ = − dΨm [ファラデーの電磁誘導の法則] dt dt
ここで,Qmの位置から見た回路Cの立体角をΩ,また,Qmの位置がduだけ移動したときのこの立体角の変化量をdΩ,また,Ψmは閉回路を貫く磁束で,
dΨm= QmdΩ =B ・dS 4π
なる関係があることはすでに前章で述べています[#]。
[5] 今,導いた[ファラデーの電磁誘導の法則]の意味するところは,
| dΩ/dt>0 (dΨm/dt>0)ならば, (=閉回路を貫く磁場が増えると,) ⇒ E の閉回路C上の線積分<0 ⇒ 閉回路Cと逆方向電場(起電力)が発生 ⇒ 閉回路Cと逆方向に電流が流れる ⇒ この閉回路CにはHMと逆方向に磁場が発生する (↑閉回路を貫く磁場を減じるような現象が生じる) |
となります。dΩ/dt<0のときはこれと全く逆の現象:「閉回路を貫く磁場が増えると ⇒ 閉回路を貫く磁場を減じるような現象が生じる」が起こります。この2つをまとめて,
| レンツの法則 導体でできた閉回路に貫く磁場が変化したときには, 「磁場の変化を打ち消すような方向に磁場を生じるような電流が閉回路に流れる。」 |
ということができます。
| [6] 一方,電場の線積分にストークスの定理 [#],および,磁束についてのΨm = |
|
|||
E ・ds= rotE ・dS
= − ∂ B・dS ∂t
とファラデーの法則を書き改めることができます。面積分の中身を比較して,ファラデーの法則の微分形,
rot E = − ∂B ∂t
が得られます。(時間微分と空間積分の順を入れ換えて,時間に関する微分は偏微分記号を用いました。)
[7] 以上,まとめると,
| ファラデー(-レンツ)の電磁誘導の法則 閉回路を貫く磁場が変化した時には,閉回路に起電力 Vf が発生し,電流が流れる。そのときの起電力は, および, [微分形] 磁束密度の変化によって生じる電場E は次式で与えられる,
[他の表現] |
これに関連した自己誘導,相互誘導については,⇒ Appendix [#]
[1] 1節で ファラデーの法則 を導く際に,「 静止している磁荷に対して速度-v で運動する電荷 Q には力 ,
F = −μ0QmQ(-v )×r = Q(-v )×μ0HM 4πμ0r3
 が働くとみなしました [#] が,これを積極的に法則として述べたものがフレミングの右手の法則です。ただし,ここでは電荷が
”主役” なので,電荷の速度(-v )を v と正のベクトルに改めて記述しましょう。すると,
が働くとみなしました [#] が,これを積極的に法則として述べたものがフレミングの右手の法則です。ただし,ここでは電荷が
”主役” なので,電荷の速度(-v )を v と正のベクトルに改めて記述しましょう。すると,
F =Qv ×μ0HM=QE
ただし,
E =v ×μ0HM=v ×B
となります。これは静磁場の中を速度v で運動する電荷 Q には
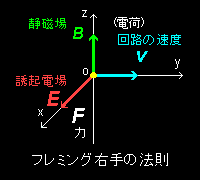
「 誘起電場 : E (中指)=v (親指)×B (人差し指) が作用する。」
 述べることができます。これらE,B,v の右図に示すような方向関係をフレミングの右手の法則と言います。
述べることができます。これらE,B,v の右図に示すような方向関係をフレミングの右手の法則と言います。
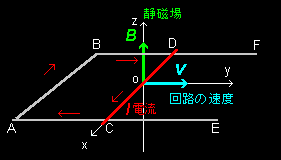
[2] さて,電荷の代わりに静磁場 ( 磁束密度B) の中におかれた右図のような電気閉回路を考えます。ここで閉回路の一部分CD
(長さL ) はAE,およびBF上をすべって,y 軸正方向へ速度v で移動するものとします。閉回路片CD の運動によってこの部分に存在している自由電子には発生した誘起電場から力が働き,その結果,電流が矢印方向に流れることになります。
(もちろん電子の流れる方向と電流の方向は逆向き)
このときの電流の方向は当然,フレミングの右手の法則から予見できる方向です。
| フレミングの右手の法則 磁束密度B の磁場に対して閉回路を速度v で動かすと閉回路には起電力が発生する。起電力の方向はフレミングの右手の法則に従い,その大きさは, |v ×B | である。 |