| Appendix B1 真空中と誘電体中での電磁波 | ||
| f-denshi.com [目次へ] 更新日: 21/10/16 リンク先のコンテンツをここに移動合体 | ||
| サイト検索 | ||
[1] 13.で示したように真空中でのマックスウェル方程式 [#]
(1) ∇E = 0 ; (2) ∇× E + ∂B = 0 ∂t
(3) ∇H = 0 ; (4) ∇×H - ∂D = 0 ∂t
から次の波動方程式が導かれます。
∂2E(r,t) = c02∇2E(r,t) ・・・・・ (1) ∂t2
∂2H(r,t) = c02∇2H(r,t) ・・・・・ (2) ∂t2
| c0 = |
|
||||||||
[2] 波動方程式の解は境界条件によって,次の2タイプの解が2つ存在します。
平面波 u(r,t) = f(k ・r -ωt+定数) 球面波
u(r,t) = 1 f(k ・r -ωt+定数) r
ここで,r = (x,y,z) は位置ベクトル,また,k = (kx,ky,kz) は位相の進行方向を向いた波数ベクトルで,波長λ,角振動数ωと,
|k | = 2π/λ,
|k | c0= 2πc0/λ=2πν = ω
ω2 = c02(kx2+ky2+kz2) = c02k2
という関係が成り立ちます。
[3] 平面波解の具体的な関数形として,
|
E (r,t )=E 0 exp [ i ( k ・r - ωt ) ] H (r,t )=H 0 exp [ i ( k ・r - ωt ) ] |
工学では虚数に負号を付けて,E (r,t )=E 0 exp [- i ( k ・r - ωt ) ] のように定義することもあります。 ⇒[#]
を考えてみましょう。
(これが(1)式の解であることは実際に代入してみれば分かりますが,有名なテクニックがあるのでこちらも見ておいてください ⇒ [#] )
この解を平面波と呼ぶ理由は,k が与えられたとき,ある 時刻 tで位相が等しい,つまり,k ・r = 一定 を満たす空間の点 (r )全体の集合が波の進行方向に垂直な平面を表すからです。
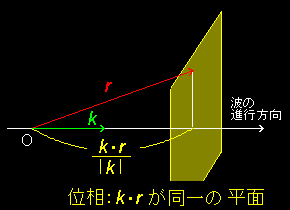
[4] この解をマックウェルの方程式(1)~(4)に代入すると,
k ・E = 0,
k ×E=μ0ωH =ωB
k ・ H =0
k ×H =-ε0ωE =-ωD
なる関係のあることも確かめられます [捕捉参照]。つまり,波の進行方向 k とE ,H の変位する方向は互いに直交しており,下のような方向関係をもった横波となります。[#]
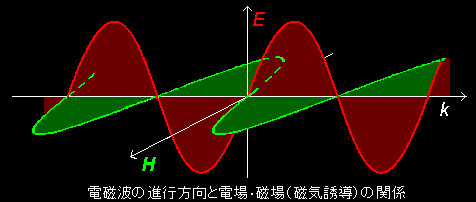
[5] 球面波については「15双極子放射の古典論」に詳述していますので,そちらを参考にして下さい。
補足 波動方程式を変形する際,
平面波: E =E0 ei (k ・r -ωt ) (H =H0 ei (k ・r -ωt ) も同様 )
(E0x expη,E0y expη,E0zexpη), η≡i [ xkx+yky+zkz-ωt ]
に下表の左側の演算子の作用は,右の演算子で代用できる。
演算子 掛け算
(1) ∂ ∂t ⇔ -i ω (2) ∇ ⇔ i k (3) ∇× ⇔ i k ×
(1)は
∂H =-i ωH ∂t
より確かにそうなっています。
(2) は,( η ≡i [xkx+yky+zkz-ωt ] として )
∇E
| = | ∂E0xexpi [xkx+yky+zkz-ωt ] | + | ∂E0yexpi [xkx+yky+zkz-ωt ] | + | ∂E0zexp i [xkx+yky+zkz-ωt ] |
| ∂x | ∂y | ∂z |
=i kxE0xexp φ+i kyE0yexp φ+i kzE0zexp φ
=i k ・E
すると,真空中では divE =0 なので,
0 = ∇E =i k ・E
と計算ができて,波数ベクトルk と電場E が直交していることが示される。
同様に波数ベクトルk と磁場H が直交していることも示されます。
(3)は
∇×E
= ∂E0zexp i [xkx+yky+zkz-ωt] - ∂E0yexpi [xkx+yky+zkz-ωt ] ∂y ∂z
, ∂E0xexpi [xkx+yky+zkz-ωt ] - ∂E0zexpi [xkx+yky+zkz-ωt ] ∂z ∂x
, ∂E0yexpi [xkx+yky+zkz-ωt ] - ∂E0xexpi [xkx+yky+zkz-ωt ] ∂x ∂y
=(i kyE0zexpη-i kzE0yexpη,i kzE0xexpη-i kxE0zexpη,i kxE0yexpη-i kyE0xexpηφ)
=i k ×E = (i k ×E 0) expη
と計算できます。すると,
∇× E + ∂B = 0 ⇒ k ×E = μ0ωH ∂t
となり,E とH が直交していることも分かります。
電磁波を,空間部分と時間部分の符号を変えて,E =E0 ei ( ωt-k ・r ) と定義している教科書(電気回路など工学系の教科書)もありますが,材料科学を主題とする「ときわ台学」では,量子力学で多く使われるここで示したような符号を採用しています。この違いは次章で複素屈折率取り扱うときに虚数部の符号の違いとなって残るのでいろいろな文献を並行して読むときには注意が必要です。悩まないように。
[1] 空気中(等方的な媒質中)では誘電率 ε=εrε0 なる誘電体中を伝わる電磁波として取り扱うことができます(エネルギー損失を無視する場合)。これは真空中の電磁場の満たす波動方程式[#]において,係数を ε0 → εrε0 と記号を置き換えること,すなわち,
c0 =
1 →
1 =
c0 = c0
εr n
ε0εrμ0
ε0μ0
とすることにすぎないので,空気中を伝播する電磁波の方程式は,
∂2E (r,t) = c02 ∇2E (r,t) ・・・・・ (3) ∂t2 n2
∂2H (r,t) = c02 ∇2H (r,t) ・・・・・ (4) ∂t2 n2
となります。ただし,ここで 屈折率 と呼ばれる,
n = εr
を定義して用いました。
[2] ここで,真空中の解を参考にして,(3)の解を
E (r,t )=E 0 exp [ i ( k ・r - ωt ) ] ( ← 真空中の k から k と換えています。)
とおいて(3)に代入してみると,
- E (r,t )ω2=-E (r,t )(c02/n 2)(kx2+ky2+kz2)
すなわち,
ω2 = c02(kx2+ky2+kz2)/n2= c02k2/n2
⇔ ω2 n2= c02k2
⇔ k2 = n2ε0μ0ω2
ただし,k =|k|,k = (kx,ky,kz )
↑ 真空中では ω2 = c02(kx2+ky2+kz2) = c02k2 でした。
を満たさねばならず,これから, ( 波の性質: ω= 2πν=2πv/λより [#] )
kc0 = nω = 2πnν = 2πnc0/λ
↓
k = 2πn/λ
なる関係も導かれます。
つまり,真空中の波数 k を,k → k/nと置き換えることで,空気中(誘電体)における各パラメータとその関係式が得られます。