 |
15 双極子放射の古典論 |
| f-denshi.com [目次へ] 最終更新日: 2016/06/02 3次元のマンガは断念して平面図で妥協した日であった。 |
| サイト検索 |
1.遅延ポテンシャル
[1] ローレンツ・ゲージ の下で,マクスウェルの方程式は電磁ポテンシャルを用いて,以下のとおりです。
| div A +εμ |
∂ψ |
= 0 [ローレンツ・ゲージ] |
|
| ∂t |
|
ここではスカラーポテンシャルについてφでなくψを用いています。(←深い意味はなく,後ほど用いる角度φとの混同を避けるため) この微分方程式の解 ψ,A がわかれば,次式から磁束密度,電場を求めることができます。
B = rot A ・・・・・・・ (1)
| E =−gradψ− |
∂A |
・・・・・・・ (2) |
|
| ∂t |
さて,時間変化のない静電場,(定常電流によって作られる)静磁場に対する電磁ポテンシャルは,
| A(r)= |
μ0 |
 |
j (s) |
d3s |
|
|
| 4π |
|r −s| |
| ψ(r)= |
1 |
 |
ρ(s) |
d3s |
|
|
| 4πε0 |
|r −s| |
|
と表すことができました[#]。ここでは,これを発展させて時間変動 (加速) のある電磁場に対する解(特解)について議論したいのですが,その形式解は,
遅延ポテンシャル
| A(r,t)= |
μ0 |
 |
j (s,t−|r −s|/c0) |
d3s ・・・ (3) |
|
|
| 4π |
|r −s| |
| ψ(r,t)= |
1 |
 |
ρ(s,t−|r −s|/c0) |
d3s ・・・ (4) |
|
|
| 4πε0 |
|r −s| |
|
で与えられ,遅延ポテンシャルと呼ばれます。この電磁ポテンシャルの厳密な導出はたいへん骨の折れる数学的作業なので,ここでは結果を鵜呑みにして話を先へ進めることにします。興味がある人はこちらを参照⇒ PDF版から抜粋 Appendix 3
[2] ここでは,この解の物理的な意味をごく簡単に述べておきます。静電場,静磁場の場合と比較すると,(3),(4)式は電流密度や電荷密度の時間変動による影響が周辺に伝わる速度が光速度であることを反映した関数となっています。すなわち,位置s にある電流密度や電荷密度といった情報が遠方の位置 r へ伝わるためには,その発生地点と受信地点との距離を伝播速度で除した, |r−s|/c0 だけの時間を要します。すると,時刻 t における位置 r の電磁ポテンシャルは,それより以前の時刻,
t’≡t−|r −s|/c0
における電荷や電流の状態を反映しているはずというのが,(3),(4)式の意味です。この時間的に遅れて伝わってくる電磁ポテンシャルの変動は遠方で電場,磁場の時間変動として観測されることになるのですが,それを電磁波(電波)と呼んでいるわけです。
2.双極子近似
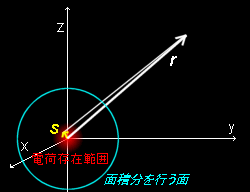 [1] 電荷が原点周りの狭い範囲(量子力学を適用するよりは大きい範囲)にだけ存在しており,遠方でその時間変化を観測する(=電波をキャッチする)ことを考えます。これは遅延ポテンシャルの積分を実行する際の数学的条件として,|r|>>|s| という近似の使用を許します。すなわち,
[1] 電荷が原点周りの狭い範囲(量子力学を適用するよりは大きい範囲)にだけ存在しており,遠方でその時間変化を観測する(=電波をキャッチする)ことを考えます。これは遅延ポテンシャルの積分を実行する際の数学的条件として,|r|>>|s| という近似の使用を許します。すなわち,
| 1 |
≒ |
1 |
 |
1+ |
r ・s |
 |
|
|
|
| |r −s| |
r |
r2 |
の置き換え[#] が可能です。このとき,遅延ポテンシャルにおける電荷密度関数は,
とおいて,
| ρ(s,t−|r−s|/c0)≒ρ |
 |
s,t− |
r |
+ |
r ・s |
 |
|
|
| c0 |
c0r |
| ≒ρ(s,tr)+ |
∂ρ(s,tr) |
・ |
r ・s |
|
|
| ∂tr |
c0r |
と近似されます。これをスカラーポテンシャルに代入すると,
| ψ(r,t)= |
1 |
 |
 |
1 |
+ |
r ・s |
 |
 |
ρ(s,tr)+ |
∂ρ(s,tr) |
・ |
r ・s |
 |
d3s |
|
|
|
|
|
| 4πε0 |
r |
r3 |
∂tr |
c0r |
| ≒ |
1 |
 |
1 |
 |
ρ(s,tr)d3s+ |
r ・ |
 |
sρ(s,tr)d3s |
+ |
r ・ |
 |
s |
∂ρ(s,tr) |
d3s |
 |
|
|
|
|
|
| 4πε0 |
r |
r3 |
c0r2 |
∂tr |
| = |
1 |
 |
Q |
+ |
r・p(tr) |
+ |
r・p’(tr) |
 |
|
|
|
|
| 4πε0 |
r |
r3 |
c0r2 |
と計算されます。ここで,
| Q= |
 |
ρ(s,tr)d3s |
| p(tr)= |
 |
sρ(s,tr)d3s |
| p’(tr)= |
 |
s |
∂ρ(s,tr) |
d3s= |
∂ |
 |
sρ(s,tr)d3s |
= |
dp(tr) |
|
|
|
| ∂tr |
∂tr |
dtr |
のように記号を定義して置き換え,|s|2に比例する項は落としました。Qは電荷の総量,また,p(tr)は電荷密度分布によって作られる電気双極子モーメントです。
[2] 次はベクトルポテンシャルについてです。位置ベクトルs=(s1,s2,s3),電流密度 j (s)=( j1(s),j2(s),j3(s) ),また,∇sをs に作用する演算子とすると,分配公式より,
| ∇s(s1j (s,t))=(∇ss1)・j (s,t)+s1(∇sj (s,t)=j1(s,t)−s1 |
∂ρ(s,t) |
|
| ∂t |
最後の=は,(∇ss1)=(1,0,0) であることと,連続の式,
| ∇sj (s,t)+ |
∂ρ(s,t) |
= 0 を用いています。 |
|
| ∂t |
この関係式を使うと,A(r,t)の x成分 A1(r,t) は|r−s|≒r,t−|r −s|/c0≒tr として
| A1(r,t)= |
μ0 |
 |
j1(s,t−|r −s|/c0') |
d3s |
|
|
| 4π |
|r−s| |
| ≒ |
μ0 |
 |
1 |
 |
∇s(s1j (s,tr))+s1 |
∂ρ(s,tr) |
 |
d3s |
|
|
|
| 4π |
r |
∂t |
| ≒ |
μ0 |
 |
∇s(s1j (s,tr))d3s+ |
μ0 |
 |
s1 |
∂ρ(s,tr) |
d3s |
|
|
|
| 4πr |
4πr |
∂tr |
と近似できます。(落とした項の吟味はここではパス)
最後式の第1項の積分は,ガウスの発散定理[#] から,
 |
∇s(s1j (s,tr))d3s= |
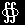 |
(s1j (s,tr)d2s |
|
|
と面積分に変換できますが,電荷が原点付近にだけに存在し,積分範囲をそれより十分大きな閉曲面上とすれば,この面積分は0となります。したがって,
| A1(r,tr)≒ |
μ0 |
 |
s1 |
∂ρ(s,tr) |
d3s |
|
|
| 4πr |
∂tr |
となります。y成分,z成分も同様に計算すると,
| A2(r,tr)= |
μ0 |
 |
s2 |
∂ρ |
d3s, A3(r,t)= |
μ0 |
 |
s3 |
∂ρ |
d3s |
|
|
|
|
| 4πr |
∂tr |
4πr |
∂tr |
ベクトルとしてひとまとめに書くと,
| A(r,tr)= |
μ0 |
 |
s |
∂ρ |
d3s |
|
|
| 4πr |
∂tr |
[3] 以上,まとめると,
双極子近似を用いた電磁ポテンシャル
| ψ(r,tr)= |
1 |
 |
Q |
+ |
r ・p(tr) |
+ |
r ・p’(tr) |
 |
|
|
|
|
| 4πε0 |
r |
r3 |
c0r2 |
|
これらがローレンツゲージを満足することの証明⇒[#]
スカラーポテンシャルの第1項は静電ポテンシャルであり,動径方向への静電場,
| E =−grad |
 |
1 |
|
Q |
 |
= |
1 |
|
Qr |
|
|
|
|
| 4πε0 |
r |
4πε0 |
r3 |
を与えます。以後はこの項については考察から除外します。
[4] 残りの時間依存性を示す項ですが,双極子がz成分しか持たず,
p(t) =(0,0,p(tr)) [双極子の成分はz 方向だけ]
と表される場合を考えてみます。そのときは,r ・p(tr)=r p(tr) cosθ (θはz軸とr とのなす角)なので電磁ポテンシャルは,
| ψ(r,tr)= |
1 |
 |
p(tr) |
+ |
p’(tr) |
 |
cosθ |
|
|
|
| 4πε0 |
r2 |
c0r |
| Az= |
μ0p’(tr) |
,Ax=Ay=0 |
|
| 4πr |
となります。さらにベクトルポテンシャルを球座標に変換する[#]と,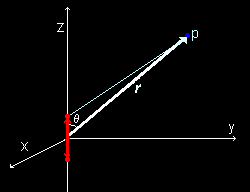
Aφ= 0
となります。一方,球座標でψの勾配[#] は,
| gradψ = |
∂ψ |
er+ |
∂ψ |
eθ+ |
1 |
|
∂ψ |
eφ |
|
|
|
|
| ∂r |
r∂θ |
rsinθ |
∂φ |
| ここで, |
∂ |
= |
∂tr |
|
|
∂ |
=− |
∂ |
であることに注意して各成分を計算すると, |
|
|
|
|
| ∂r |
∂r |
∂tr |
c0∂tr |
| ∂ψ |
= |
1 |
 |
− |
2p(tr) |
+ |
-p’(tr) |
− |
p’(tr) |
+ |
-p’’(tr) |
 |
cosθ |
|
|
|
|
|
|
| ∂r |
4πε0 |
r3 |
c0r2 |
c0r2 |
c02r |
| = |
-1 |
 |
p(tr) |
+ |
p’(tr) |
 |
− |
p’’(tr) |
cosθ |
|
|
|
|
| 2πε0 |
r3 |
c0r2 |
4πε0c02r |
| ∂ψ |
= |
1 |
 |
p(tr) |
+ |
p’(tr) |
 |
(-sinθ) |
|
|
|
|
| r∂θ |
4πε0 |
r3 |
c0r2 |
また,
| ∂Ar |
= |
μ0p’’(tr) |
cosθ= |
p’’(tr) |
cosθ |
|
|
|
| ∂t |
4πr |
4πε0c02r |
| ∂Aθ |
=− |
μ0p’’(tr) |
sinθ=− |
p’’(tr) |
sinθ |
|
|
|
| ∂t |
4πr |
4πε0c02r |
よって,
| = |
1 |
 |
p(tr) |
+ |
p’(tr) |
 |
cosθer |
+ |
1 |
 |
p(tr) |
+ |
p’(tr) |
+ |
p’’(tr) |
 |
sinθeθ |
|
|
|
|
|
|
|
| 2πε0 |
r3 |
c0r2 |
4πε0 |
r3 |
c0r2 |
c02r |
磁場については,球座標の回転[#] を計算して,
B=rotA
| = |
 |
∂(sinθAφ) |
− |
∂Aθ |
 |
er + |
 |
∂Ar |
− |
∂(rAφ) |
 |
eθ + |
 |
∂(r・Aθ) |
− |
∂Ar |
 |
eφ |
|
|
|
|
|
|
| rsinθ∂θ |
rsinθ∂φ |
rsinθ∂φ |
r∂r |
r∂r |
r∂θ |
| = |
 |
∂ |
 |
μ0p’(tr) |
sinθ |
 |
|
| 4π |
|
− |
∂ |
 |
μ0p’(tr) |
cosθ |
 |
|
| 4πr |
|
 |
eφ |
|
|
| rc0∂tr |
r∂θ |
| = |
μ0 |
 |
p’’(tr) |
+ |
p’(tr) |
 |
sinθeφ ≡Bφeφ |
|
|
|
| 4π |
c0r |
r2 |
したがって,十分遠方においては,r-2以下の項を小さな寄与として落し,
| Eθ= |
p’’(tr) |
sinθ |
|
| 4πε0c02r |
| Bφ= |
μ0 |
|
p’’(tr) |
sinθ |
|
|
| 4π |
c0r |
|
他の成分は 〜0 |
を得ます。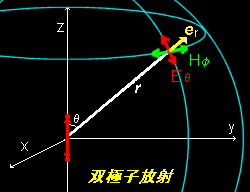 すなわち,伝播する電磁波は,θ方向で電場が振動し,φ方向で磁場が振動しており,その振幅は
r に反比例しながら減衰していくことがわかります。これはr2に反比例して減衰する静電場より,遠くまでその影響が及んでいることを意味しています。
すなわち,伝播する電磁波は,θ方向で電場が振動し,φ方向で磁場が振動しており,その振幅は
r に反比例しながら減衰していくことがわかります。これはr2に反比例して減衰する静電場より,遠くまでその影響が及んでいることを意味しています。
[5] さらに,明確に示すために,ポインティングベクトル[#]を計算すれば,
Pt=E ×H
| = |
p’’(tr) |
sinθeθ× |
p’’(tr) |
sinθeφ |
|
|
| 4πε0c02r |
4πc0r |
| = |
|p’’(tr)|2sin2θ |
er |
|
| 16π2ε0c03r2 |
|
となり[#],r方向(動径方向)に輻射エネルギーが流れていることがわかります。その強さは方向依存性を持ち,θ=90°方向でもっとも強く,z軸に沿った方向ではゼロです。つまり,
「双極子(電荷)の変動(加速)方向とは垂直の方向へもっとも強い光が放射される。」
ということに注意してください。右図を参考にしてください。
遠方での球面上(半径R)で積分[#]すれば,
| W = |
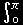 |
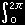 |
(Pt ・er)R2sinθ dφdθφ |
| =2π |
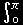 |
|Pt| |
R2sinθdθ |
| = |
|p’’(tr)|2 |
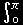 |
sin3θdθ ← |
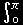 |
sin3θdθ = 4/3 |
|
| 8πε0c03 |
| = |
|p’’(tr)|2 |
・・・・[*] |
|
| 6πε0c03 |
ここで,「z方向に単振動する双極子」 からの放射エネルギーは,p=p0s inωt として時間平均をとると,
| <W>= |
p02ω4 |
|
<sin2ωt> ← |
1 |
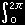 |
sin2t dt= |
1 |
|
|
|
| 6πε0c03 |
2π |
2 |
| = |
|p0|2ω4 |
双極子放射エネルギー |
|
| 12πε0c03 |
これは,電気双極子の単振動によって放出される単位時間当たりのエネルギーとなっています。
また,[*]で,p=Qz(t)として,
| W= |
Q2 |
(z’’(t))2 Larmorの公式 |
|
| 6πε0c03 |
これは電荷がz方向で加速された際にその加速度の2乗に比例したエネルギーをもつ電磁波が放出されることを表していますが,電荷の任意の加速運動にも拡張することができ,Larmorの公式と呼ばれます。
最後に荷電粒子の加速による電磁波放出の重要な例 (v/c<<1のとき) を2つマンガにしておくと次のようになります。
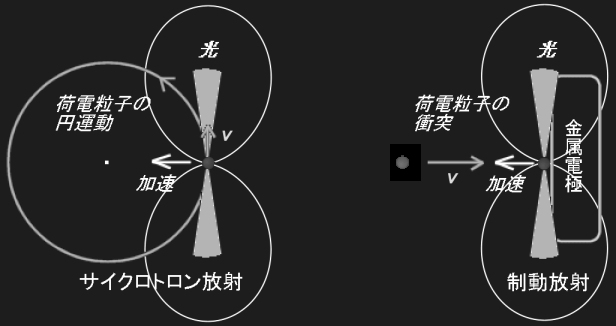
とりあえず,ここまで。
量子論的な取り扱いは ⇒ [#]
[目次へ]
 [1] 電荷が原点周りの狭い範囲(量子力学を適用するよりは大きい範囲)にだけ存在しており,遠方でその時間変化を観測する(=電波をキャッチする)ことを考えます。これは遅延ポテンシャルの積分を実行する際の数学的条件として,|r|>>|s| という近似の使用を許します。すなわち,
[1] 電荷が原点周りの狭い範囲(量子力学を適用するよりは大きい範囲)にだけ存在しており,遠方でその時間変化を観測する(=電波をキャッチする)ことを考えます。これは遅延ポテンシャルの積分を実行する際の数学的条件として,|r|>>|s| という近似の使用を許します。すなわち,
 すなわち,伝播する電磁波は,θ方向で電場が振動し,φ方向で磁場が振動しており,その振幅は
r に反比例しながら減衰していくことがわかります。これはr2に反比例して減衰する静電場より,遠くまでその影響が及んでいることを意味しています。
すなわち,伝播する電磁波は,θ方向で電場が振動し,φ方向で磁場が振動しており,その振幅は
r に反比例しながら減衰していくことがわかります。これはr2に反比例して減衰する静電場より,遠くまでその影響が及んでいることを意味しています。