| 13-1 電磁場のエネルギー | ||
| [目次へ] 更新日: 16/05/25 | ||
| サイト検索 | ||
[0] マクスウェルの方程式をもう一度書いておくと,
(1) divD =ρ 電荷のガウスの法則 [#]
(2) rotE =− ∂B ∂t ファラデーの法則 [#] (3) divB =0 磁荷のガウスの法則 [#]
(4) rotH = ∂D +j ∂t アンペールの法則 [#]
また,物質中では,
D = μ0E +P , B = μ0H +M
の関係が成り立ちます。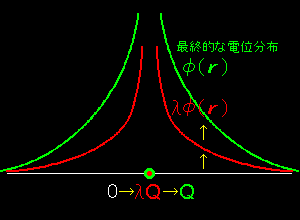
[1] ここでは,電磁場に蓄えられるエネルギーを考察していきたいのですが,もっとも簡単な例として,非常に小さな導電性の球体に,無限遠から素電荷を一つずつ運んで,最終的に電荷Qが均一に球表面に分布する状態 (=系と呼ぶ) を作り出す過程を考えます。このとき,2つ目以後の素電荷を無限遠から球体へ運ぶためには,それまでに球体へ運んである電荷との間の反発に逆らって,仕事をする必要があります。したがって,一定の領域に電荷が集まった状態を作り出すためには,系にエネルギーを与える必要があり,これは見方を変えれば,複数の素電荷から構成される系にはエネルギーが蓄えられていると考えることができます。そのエネルギーはどれか特定の電荷に帰着させるよりは,そこに形成されている電場に蓄えられているエネルギーと考える方が自然です。
(上の説明は,複数の素電荷からできている系を念頭においていますが,素電荷一つだけからなる系 ,たとえば,宇宙に電子一個だけが存在しているような場合 についても,それが無限小の電荷を無限遠から寄せ集めてできていると考えば,素電荷,もしくはそれが作り出す電場にエネルギーが蓄えられていると考えることができます。つまり,電荷はそれが存在するだけでエネルギーを持っていると考えることができるのです。)
[2] そこで,そのエネルギー量を一般的な電荷分布状態について計算してみましょう。すなわち,最終的に到達すべき電荷分布 ρ(r ) にいつも比例するように,
0 ⇒ λρ(r ) ⇒ ρ(r ) ( λ: 0 → 1 )
と電荷を空間に増やしていく様子を考えます。 電荷分布がλρ(r )のとき,電位分布関数は,λφ(r )と表せしことができますが,さらにdλρ(r )だけ電荷密度を増加させるために必要な電荷量は,
dQ= dλρ(r )dV
と書くことができます。また,これだけの電荷を増加させるために必要なエネルギー dW は,
dW = (λφ)(dλρ(r )dV) = λdλ φ(r )ρ(r )dV
となります。積分は全空間にわたって行ないます。 したがって,電荷分布ρ(r )を形成するために必要なエネルギーは,これをλ=0 から 1 まで積分すればよく,
| W = | λdλ | φ(r )ρ(r )dV = | 1 | φ(r )ρ(r )dV = | 1 | φ(r ) div D dV | ||||
| 2 | 2 |
| = | 1 | φ(r ) | ∂Dx | + | ∂Dy | + | ∂Dz | dV | |||
| 2 | ∂x | ∂y | ∂z |
この第1項を x について部分積分すれば,
| 1 | φ(r ) | ∂Dx | dV = | 1 | [φDx] | − | ∂φ | Dxdx | dydz ← φDx=0 at x=±∞ | ||||||||
| 2 | ∂x | 2 | ∂x | ||||||||||||||
| = | 1 | ExDxdV ; ここで,Ex= | ∂φ | 電場の x 成分 | ||
| 2 | ∂x | |||||
第2,3項も同様で,結局,電界に蓄えられるエネルギー は E と D の内積の積分として,
W = 1 E ・D dV [ 電界に蓄えられるエネルギー ] 2
で与えられます。要するに,無限遠から微小電荷を寄せ集めてきて,ある電荷分布形成するために必要なエネルギーは,最終的な電荷分布が作り出す電場について,全空間にわたる上式の積分を行えばよいということです。また,被積分関数に着目して言い換えると,電場のもつ体積エネルギー密度は,空間の各点において,
1 E ・D [ 電界に蓄えられているエネルギー密度 ] 2
であると考えてもよいでしょう。
[3] 磁場に蓄えられる体積エネルギー密度についても同様に考えて,
1 H ・B [ 磁界に蓄えられているエネルギー密度 ] 2
とすることができます。以上をまとめると,電場,磁場に蓄えられるエネルギーは,
|
真空や均一な媒体(空気,水など)中のように,電場と電気変位の関係,磁場と磁束密度との関係が比例関係,
E ∝ D,H ∝ B ← もっとはっきりと書けば,D = εE, B = μH
で十分近似できるときは,
E ・D =εE2 , および,H ・B =μH2
と書くことができるので,
W = 1 (εE2+μH2 ) dV 2
と表すこともできます。
[4] 一方,体積 V 内にある電磁場エネルギーの時間変化は,
∂W = {E ・ ∂D + H ・ ∂B }dV ∂t ∂t ∂t
↓ 実在電荷,実在電流のない時のマクスウェルの方程式 [#]
= { E ・( rot H )+H ・(−rot E )} dV
↓ ベクトル解析の公式 2-(2) [#]
= div(H ×E ) dV
↓ガウスの定理 [#]
= (H ×E )n dS
これは単位時間に単位面積を垂直方向に出ていく(電磁波の)エネルギーが,
Pt ≡ (E ×H )
で与えられることを意味しています。これをポインティングベクトルと言います。
[5] ポインティングベクトルがエネルギーを運ぶ実態であることの説明は次の動画を参考にして頂くとよく理解が深まると思います。
[6] 次に磁化,電気分極をもつ物質が存在する一般的な場合について考えます。先程の公式
div (E ×H )=H ・rotE −E ・rotH
において,マクスウェルの方程式(2),(4)を代入すると,
=H ・ − ∂B −E・ ∂D +j ∂t ∂t
すなわち,
H ・ ∂B +E・ ∂D =−E ・j − div (E ×H ) ∂t ∂t
ここで,この式に磁気誘導と磁化,および,電気変位と電場が必ずしも同じ方向を向いていない一般的な場合に成立する関係式,,
B = μ0H +M , D =ε0E +P
を代入すると左辺は,
| H ・ | ∂ | (μ0H +M )+E ・ | ∂ | (ε0E +P ) =μ0H ・ | ∂H | +ε0E ・ | ∂E | +H ・ | ∂M |
+E ・ | ∂P | ||||||
| ∂t | ∂t | ∂t | ∂t | ∂t | ∂t | ||||||||||||
となります。したがって,
1 ∂ (μ0H 2+ε0E 2)+H ・ ∂M
+E ・ ∂P +div (E ×H )=−E ・j 2 ∂t ∂t ∂t
すなわち,
∂u(場) + ∂u(物) =−div (E ×H ) −E ・j ・・・[*] ∂t ∂t
ただし,
u(場) = 1 ( μ0H 2+ε0E 2 ) [電磁場のエネルギー密度] 2
∂u(物) =H ・ ∂M +E ・ ∂P ∂t ∂t ∂t
ここで,u(物)は「物質の電磁気的(内部)エネルギー密度」を意味しており,[*]は熱の発生,損失のない「断熱条件下」でのエネルギー保存則を表しています。
ここに出てくる E ・j については,これをジュール熱としている教科書やネット上のサイトもありますが,それでは不正確だと思います。 E ・j の意味することは電場が電荷に対して行う(符号付で/単位時間・単位体積当たり)の仕事ということ以上のことはわからないはずです。そもそもマクスウェルの方程式は熱の概念を含んでいません。
ジュール熱が発生するというのは,電場が電子に対して行った仕事が,物質の(イオン)格子振動に変換されることをいうのであって,かなり複雑です。発光ダイオードでは,このE ・j は熱の生成だけでなく,光の生成にも使われるはずです。PN接合部では電子は静電エネルギーを失い,電磁波を放出しているわけでしょう。E ・j はデバイスをイメージするときに限るならば,系に投入される電力密度とすることが違和感ないと思います。(以上,注意喚起 2016/5/25)
熱の発生,損失を考慮するときは,熱力学的な全内部エネルギー密度 u(熱力学的) の変化は,u(物) など電磁気現象由来の変化だけでなく,固体ならば原子の振動エネルギーなどいわゆる力学的エネルギーu(熱)も考慮する必要があり,
du(熱力学的)≡du(場)+du(物)+du(熱)
とすべきです。また,外部との熱のやり取りで内部エネルギーも変化しますので,正しいエネルギー収支は,熱力学第1法則(単位時間あたり),
| 系の内部エネルギーの増加 | = | 系に加えられた仕事 | + | 系に加えられた熱量 |
| dU | d'W | d'Q |
によって与えられるはずです。したがって,[*]式は,系の受け取る熱をdqとすると,
∂u(場) + ∂u(物) + ∂u(熱) =−div (E ×H ) −E ・j + ∂q ∂t ∂t ∂t ∂t
と修正しなければいけません。系の体積でこれを積分形して,divの部分は表面積分に書き換えれば,
| ∂U(場) | + | ∂U(物) | + | ∂U(熱) | =− | |
(E ×H )・dS | − | |
E ・j dV+ | ∂Q | ・・・ [**] | ||||||||
| ∂t | ∂t | ∂t | ∂t | |||||||||||||||||
↑ 先の記号 u,q の系全体にわたる積分値を大文字 U,Q で示しています。
となります。極端な場合として,[**]式で左辺がゼロの (例えば,抵抗回路に定常電流が流れていて,電荷分布に変動がなく,物体の温度上昇もない)ときで,光も放出されていない状況であれば,
− E ・j dV=− ∂Q ∂t
となります。これは,系に投入された電力∫(−E ・j )dV がすべてジュール熱∂Q/∂t となって放散されていることを示しています。
ところが,もし,効率100%の発光ダイオードがつながれた回路に電気を通じているのであれば,[**]式は,
− E ・j dV = (E ×H )・dS
となりますが,これは投入された電力が電磁波となって系外へ放出されていることを示しています。