| Appendix C1 遅延ポテンシャルの導出 | |
| f-denshi.com [目次へ] 最終更新日: 2021/09/15 | |
| サイト検索 | |
本文中で割愛した遅延ポテンシャル [#] の計算方法を示します。
[1] ローレンツゲージ下の電磁ポテンシャルに対する波動方程式のうち,スカラーポテンシャルψ (r, t) に対する式 [#] を少し書き直して再掲すると,
スカラーポテンシャルの満たすべき方程式
∂2 −Δ ψ(r,t)−ρε(r,t)= 0 (1) c2∂t2
ただし, ρε(r,t)≡ ρ(r,t) とおいた ε
[2] この波動方程式の一般解を求めてみましょう。道具立てですが,ψ(r,t),ρε(r,t) を k,ω空間における関数 Ψ(k,ω),P(k,ω) のフーリエ変換として次のように表しておきます。
ψ(r,t)= eiωt e- ik ・r Ψ(k ,ω) d3k dω (2)
ρε(r,t)= eiωt e- ik ・r P (k ,ω) d3k dω (3)
一方,ρε の逆フーリエ変換は,(後の計算で紛れないよう,空間を s ,時間をτで記述する。)
P(k ,ω) = 1 e-iωτ+ ik ・s ρε(s,τ)d3s dτ (4) (2π)4
と書くことができます。
まず,(2),(3) を(1) に代入して,時間 t,空間 r ( Δ ) に関する2階微分を実行しておけば,
eiωt- ik ・r { (-ω2/c2+k2)Ψ(k ,ω) − P(k ,ω) }d3k dω = 0 (5)
この式から得られる{(-ω2/c2+k2)Ψ(k ,ω) − P(k ,ω) }=0 をΨ について解けば,
Ψ(k ,ω) = P(k ,ω) (6) k2 −ω2/c2
これを(2) に代入してΨ(k,ω) を消去すれば,
ψ(r,t)= eiωt- ik ・r P(k ,ω) d3k dω (7) k2 −ω2/c2
[3] さらに,(4) を (7) に代入して,P(k,ω) を消去すれば,
グリーン関数による遅延ポテンシャルの積分表示
ただし,
|
||||||||||||||||||
ここで,G(r −s,t−τ) はグリーン関数と呼ばれます。G が分かれば,与えられたρε からψ(r,t) を計算することができます。(要するに,微分方程式の解を積分表示して,積分の問題に置き換えているのです。)
[4] では,グリーン関数の積分を求めましょう。まず,R =r−s,T=t−τとおき,
G(R,T)≡ 1 eiωT- ik ・R d3kdω (2π)4 k2 −ω2/c2
として計算を進めますが,k 空間の部分を球座標で書き直すと,(R をz 方向にとり,R = |R| とする。dk3⇔ k2dk dφdcosθ )
G(R,T)= 1 dω dk dφ dcosθ k2 eiωT- ikRcosθ (2π)4 k2 −ω2/c2
↓ φとcosθに関して積分を実行すれば,
= 1 dωeiωT dk -1 (e-ikR−eikR) k (2π)3 iR k2 −ω2/c2
↓ dk -ke-ikR = dk keikR k2 −ω2/c2 k2 −ω2/c2
= 1 dωeiωT dk eikR 1 + 1 (9) 2(2π)3iR k+ω/c k−ω/c
となります。
ところが,このままでは k 上の特異点で関数が発散するため積分値がわかりません。そこで,特異点の回避のため,ψ をψeαt, (α > 0) で置き換える,すなわち,ω → ω- iαで置き換える技巧を用いて解決することとします。この変更の物理的な意味は十分な(無限大の)過去 (t→-∞) においては電場(波動)がなかった (ψ(r, -∞)=0 ) という条件を満たす解に限定して方程式を解こうということです。
( しかしながら,後に,α → +0 とすることで,広い一般性が付与されます。)
[5] この置き換えによって計算すべきk に関する積分は,
| I = | g(k) dk | = | dk | eikR | 1 | + | 1 | |||||
| k+ω/c−iα/c | k−ω/c+iα/c | |||||||||||
| g(k) | ||||||||||||
となりますが,この積分は複素解析における「留数定理」を利用して求めることができます。
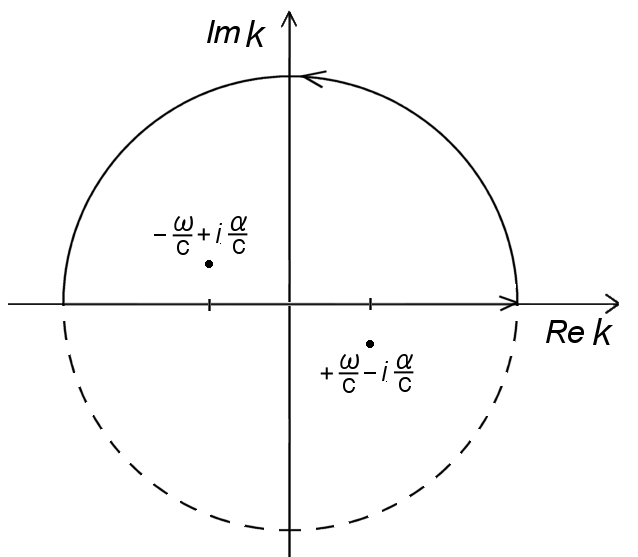
I の積分経路
積分経路をループとするために,k の複素平面の正虚数部に半円を付け足した経路で積分を行えば,経路内に1 位の極が,k=−ω/c+iα/c に一つあることに注意して,留数定理 [#] から,
g(k) dk=2πi・Res [g(k),−ω/c+iα/c]
=2πi・ lim (k+ω/c−iα/c) g(k) k → -ω/c+iα/c
=2πi・
lim k → -ω/c+iα/c eikR 1+ k+ω/c−iα/c k−ω/c+iα/c
=2πi ・ei (-ω/c+iα/c)R
であることが分かります。
[6] さらに,半円周Γ 上の積分値が半径 → ∞ で 0 と見積もれる [#] ことから,α → 0 としたすぐ上の積分値を (9) に代入すれば,
G(R,T)= 1 dωeiωT・2πi・e-iωR/c 2(2π)3R
= 1 1 dωeiω(T−R/c) 4πR 2π
ここで,デルタ関数 [#] ,
δ(T−a)= 1 dωeiω(T−a) [デルタ関数] 2π
を用いれば,
G(R,T)= 1 δ(T−R/c) 4πR
= 1 δ(t-τ−|r -s|/c) 4πR
≡ G(r -s,t-τ)
と書けます。
[7] これを (8) [*] に代入して,デルタ関数δ(T−a) の性質,
δ(T−a)f(T)=f(a)
を用いれば,
ψ(r,t)= d3s 1 δ(t-τ−|r -s|/c)ρε(s,τ)dτ 4π|r −s|
= d3s ρε(s,t−|r −s|/c) 4π|r −s|
= 1 ρ(s,t−|r −s|/c) d3s 4πε0 |r −s|
が得られます。これが双極子放射の計算に用いた遅延 (スカラー) ポテンシャルの(4)式 [#] です。
以上で導出終わりです。
[8] 計算の途中でα>0 を導入して特異点を回避しました [#] が,α<0 としても特異点を避けて積分値を得ることができます。符号がところどころ反転するだけで同じような計算をして,
ψ(r,t)= 1 ρ(s,t+|r −s|/c) d3s 4πε0 |r −s|
が得られます。これを先進ポテンシャルと呼ぶこともあります。
ご覧のように「双極子放射の古典理論」は物理数学の初級から中級の知識を総動員して初めて理解できるので,それらをきちんと理解して使いこなせるかどうかの認定試験のようですね。
ベクトル解析からテーラー展開,球座標変換
複素関数論から留数定理
関数論からフーリエ変換,デルタ関数,グリーン関数法
などなど