| 4 電位 | ||
| f-denshi.com [目次へ ] 最終更新日:21/10/19 | ||
| サイト検索 | ||
[1] まず,ベクトル解析の結果[#]を引用すると,
「 なめらかな(閉)曲面の方程式が,「 φ(x,y,z)−c = 0 ; c 定数 」と表されているとき,この曲面上の単位法線ベクトル[#]は,
n ( x,y,z ) = 1 ( φx,φy,φz )
(φx)2+(φy)2+(φz)2
と表すことができる。 」
ここで,φx はφ の x に関する偏導関数,他も同様です。また,ベクトル,
(φx,φy,φz) = ∂φ , ∂φ , ∂φ = grad φ=∇φ ∂x ∂y ∂z
は関数 φ(x,y,z) の勾配(グラジエント)[#] と呼ばれます。 なお,係数の[(φx)2+(φy)2+(φz)2]-1/2 はn (x,y,z)の大きさを1とするための規格化因子で,ここでの議論ではあまり重要ではありません。
数学的な意味はφ(x,y,z)の変化率(傾き)が最も大きな方向を示す単位ベクトルn と言うことですが,2次元f(x,y) で考えた方が分かりやすいので,こちらを参考にして下さい ⇒ 方向微分係数と勾配
[1-2] 単位法線ベクトルの定義式を少し言い直して,
「 φ ( x,y,z ) = c (一定) なる曲面上の点(x,y,z) で勾配ベクトル(φx,φy,φz) を考えると,このベクトルはこの曲面に(必ず)直交している。 」
(ここで,φ ( x,y,z )=c は曲面の方程式であって,定数関数という意味ではない!)
とすることができます。もちろん180°反対を向いたベクトル (−φx,−φy,−φz ) も曲面とその点で直交しています。
そこで,電場ベクトルE (x,y,z)に対して,
−gradφ=(−φx,−φy,−φz) =E (x,y,z)
を満たすような φ(r )≡φ(x,y,z) を考えると,電場 E =(−φx,−φy,−φz ) は φ(r )=c (定数) となる曲面に垂直となっていることがわかります。このようなφ(r )を静電ポテンシャル(関数),その値 c を電位といいます。
ここで,わざわざマイナスの符号が付くように定義するのは,φ( =c ) が減少する方向を電場の正方向と一致させたいためです。 (そうすると,電場中に置かれた ”正電荷” に働く力の方向と電場の方向が一致して気分がいい!)
| 電位の定義 電場E (r ) に対して, −grad φ(r ) = E (r ) を満たすような φ(r ) を電場E (r ) の静電ポテンシャル(関数),その値 を電位という。 |
また,ある一つの c に対する φ(r ) =c で表される曲面を等電位面といいます。いろいろなc について考えるとそれに対応する等電位面が一つ定まり,一連の曲面群を作ります。電場はこれらすべての等電位面に垂直であり,各点で電位の最も小さくなる方向を向いています。
なお,φ(r )が電場E (r )の電位であるならば,gradχ(r )=0 となるχ(r )を付加したφ(r )+χ(r ) もE (r )の電位です。つまり,電位はこの定義だけから一意的に定まる関数ではありません。どこかに基準点を定めることによって一意的に定まるのです。なお,実際にgradφ(r ) が存在するかどうかの数学的な判断は,ストークスの定理(の系)[#]によります。
[1-3] 3変数関数 φ(x,y,z) を図示するには4次元空間が必要で,直感が働きにくいので,2変数関数 f(x,y) で考えてみます。具体例として地形図を思い浮かべます。

この場合,h=f(x,y) は地点 (x,y) の標高 h を意味します。図形 f(x,y)=c は等高線で,標高 h=c である曲線の方程式です。そして,grad (x,y) は地点の傾斜(最もきつい登り方向)を意味します。電磁気学との対応は,次のとおりです。
h=f(x,y) 標高 ⇔ φ=φ(r ) 電位,静電ポテンシャル
f(x,y)=c 等高線 ⇔ φ(r )=c 等電位面
grad f(x,y) 傾斜 ⇔ −gradφ≡E (x,y,z) 電場
イメージつかめたでしょうか?
[2] 次に,具体的に原点にある点電荷 Q の作る電場の電位を求めてみましょう。いま,電場を
E = kQ ・ r |r | 3
とすると[#],電位 φ(r ) を,
φ (x,y,z) =φ (r )= kQ ・ 1 |r |
 とすれば,−gradφ = E を満足することが簡単な計算からわかります。
とすれば,−gradφ = E を満足することが簡単な計算からわかります。
⇒ 位置ベクトルの微分公式(1)でn=-1とする[#]。
先ほど述べたように,このφ に gradχ =0 なる項χ(積分定数) を加えてもよいのですが,ふつうは,r → ∞ で電位が 0 となるようにこの項を 0 と定めます。これを,
「電位の基準 0 を無限遠に定める。」
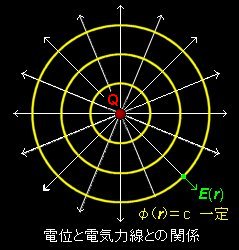
という言い方をします。また,電位 φ(x,y,z) = c (一定)となる等電位面,すなわち,点電荷からの距離|r|が一定値となる面を考えると,これはいろいろな半径 r をもつ球面,x2+y2+z2=r2 (r>0) の集合であることがわかります。その球面上の位置r における法線ベクトル[#]は,
n ( x,y,z ) = ( 2x,2y,2z ) =r /|r |∝E
(2x)2+(2y)2+(2z)2
であることも確かめられます。したがって,電場と等電位面の関係は右図のようになっています。
点電荷ではなく,多数の電荷が ρ(s) で分布している場合は,スカラー量であるφは単純な足し算ができるので,
φ (r )= k ρ(s) ds |r −s |
と積分で表すことができます。
 [3] ここまで φ を数学的な技巧として導入して説明してきましたが,このφには,
(静電ポテンシャル)エネルギーという物理的な意味を持っています。
[3] ここまで φ を数学的な技巧として導入して説明してきましたが,このφには,
(静電ポテンシャル)エネルギーという物理的な意味を持っています。
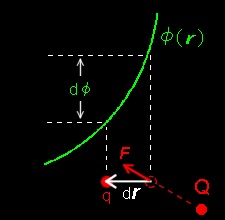
この事実は,ある点から dr 離れた点へ電荷q を運ぶときに,力 F=qE が行う仕事(=エネルギー) dW が,
dW = F ・dr
= qE ・dr
= −q (φxdx+φydy+φzdz)
=q ∂φ dx+ ∂φ dy + ∂φ dz ∂x ∂y ∂z
=−q (dφ)
のように計算されることからわかります。
(↑ 単位 [V]の定義: [N][m]=[C][V] から決まります。)
ここで,電場ベクトルを E =(−φx ,−φy ,−φz ),位置の微小変位を dr = (dx,dy,dz) としています。
[4] 上の最後の等号=は数学的にはφが全微分可能である場合に成り立ちます。このとき,3次元空間の点P からQ へ電荷 q を運ぶための仕事 W は積分:
W= F ・dr = −q dφ =−q {φ(Q)−φ(P)}
で求まり, (↑積分記号が多少アバウトですが,意味は汲み取れますね?)
”電荷を運ぶ仕事は途中の経路によらず,始点と終点のポテンシャルだけで決まる。”
ことがわかります。
つまり,ポテンシャルを導入することで,エネルギー変化を求めるための計算が,左辺の線積分[#]から右辺のようなタダの数(スカラー)の引き算に帰着できるというメリットがあるのです。
数学的な言葉でいうと,ベクトル値関数E (r)よりスカラー関数φ(r)の方が取り扱いがずっと楽なんです。そして必要であれば,φ(r)の勾配(=微分の計算)を計算することで電場E (r) は簡単にも求められるのです。積分より微分の方がずっと簡単でしょう?
[5] いま,電場E が各変数について微分可能で,その導関数が連続とします。点電荷の場合,電荷の置かれた r = 0 の点を除けば確かにそうなっています。また,この条件は,電位 φ にとっては,2回連続微分可能なC2級関数[#]ということになります。
このとき,次のE =(Ex,Ey,Ez) ←電場成分 の回転( rot E,または,∇ × E ) と呼ばれる(ベクトル)量 [#]
rotE= ∂Ez − ∂Ey , ∂Ex − ∂Ez , ∂Ey − ∂Ex ∂y ∂z ∂z ∂x ∂x ∂y
を考えてみましょう。 E =−( φx,φy,φz ) として, ←φxはφのxに関する微分などという意味。
| rot E =− | ∂φz | − | ∂φy | , | ∂φx | − | ∂φz | , | ∂φy | − | ∂φx | ||
| ∂y | ∂z | ∂z | ∂x | ∂x | ∂y |
=−( φzy−φyz,φxz−φzx,φyx−φxy )
とφの2階偏導関数で表せます。ところが, C2 級関数についての解析学の教えから2階微分の順序は交換可能であり,
φzy=φyz,φxz=φzx,φyx=φxy
が成り立ちます[#]。すなわち,rot E の成分はすべてゼロで,
| 点電荷の作る電場の回転 (r =0 の点を除く) rot E =0 (零ベクトル ) |
となります。
ベクトルの回転がゼロというのはベクトル場E (r ) が渦を巻いていないという意味で,
より深い理解のためには ⇒ ・渦,湧き出しのない2次元ベクトル場 [#1],
(↑では 電場=流れ関数)
・ストークスの定理 [#2] を参照のこと
これは,言い換えると,
「電気力線は,r=0 の点以外では発生,消滅しない。
⇔ 発生・消滅場所は電荷の存在する点だけである。」
という事実にも対応しています。(r =0 の点ではポテンシャル関数は微分できない!)
[6] 一方,E = −grad φ をガウスの定理の微分形 [#]: divE =ρ(r) /εに代入すると,
divE =− ∂φx − ∂φy − ∂φz ∂x ∂y ∂z
=− ∂2φ + ∂2φ + ∂2φ ≡ −Δφ ∂x2 ∂y2 ∂z2
となり,ポアソン方程式と呼ばれる次の微分方程式が得られます。
[ ポアッソン方程式 ]
特に,点電荷の場合は, ρ(r ) = Qδ(r ) とかけるので, ( デルタ関数 ⇒ [#] ) −Δφ = ρ(r ) / ε= Qδ(r )/ε
|
また, ポアッソン方程式で,ρ(r ) = 0 ( 右辺 = 0 ) とした微分方程式をラプラス方程式と呼び,
Δ≡∇2 ≡ ∂2 + ∂2 + ∂2 ∂x2 ∂y2 ∂z2
はラプラス演算子と呼ばれます[#]。
ここで,divE≠0 ということは,ベクトル解析の知見を借りれば,ベクトル場E (r) に湧き出しがある [#1] ということで,
「電気力線は,ρ(r)≠0 の点で発生,消滅する。」
ということに対応しています。点電荷であれば,δ(r )≠0,すなわち,r =0 の点でだけ電気力線は発生・証明することを表しています。
[7] 最後に電位差と電圧の定義を書いておきましょう。
位置 r1,r0 の電位φ( x1,y1,z1 ),φ( x0,y0,z0 ) について,
φ(x1,y1,z1)−φ(x0,y0,z0)
を電位差といいます。またその絶対値,
V =|φ(x1,y1,z1)−φ(x0,y0,z0)|
を電圧と呼びます。単位は [V] です [#]。
[1] 金属のように両端に電圧をかけて連続的に電気を流し続けられる物質を導体,そうでない物質を不導体,絶縁体,または誘電体といいます。
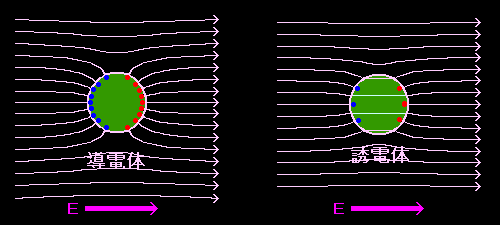
下図は均一な電場の中に球状の導体と誘電体を置いたときの物質内外の電気力線の様子を示しています。導体内部に電場は全く侵入できないのに対して,誘電体中にはいくらか電場が進入している様子(模式図)を描いています。
[2] なぜこのように描くかと言うとと,導体中には自由電子と呼ばれる導体内部を自由に移動できる電子が多数存在します。従って,もし導体内部に電場が存在すると,その電場によって導体中の電子が力を受けて移動し,
(1)最終的に電子は境界(導体表面)に集まり,その電荷分布が作る電場と外部の電場が導体内部で完全に打ち消し合ってゼロとなったとき,はじめて電子の移動は止み,電荷分布は安定します。
この様子を
「導体内部には電気力線が侵入できない」
という言い方で表現します。もう一つの特徴は導体内部に電場が存在しないということは,
(2)導体内部の電位はすべて等しいことを意味します。
したがって,
(3)導体表面で発生・消滅する電気力線は導体表面(=等電位面)に垂直[#]でなければいけません。
それで電気力線は右上のように導体表面に直交するように描かれます。
[3] 一方,誘電体中で電子は個々の分子や原子に強く束縛されており,誘電体内部に電場が存在しても電子は分子・原子の束縛の範囲内でしか変位(小さな移動)しません。この変位によってできた電場は外部電場の一部を打ち消すように働きますが不完全です。つまり,
「誘電体内部には電気力線が一部侵入する」
と言うことができます。その様子は図で示したようになります。
V [V] =[N][m][C]-1