13-2 　電場・磁場の応力
f-denshi.com ［目次へ］　更新日： 03/05/26
サイト検索

電荷をもつ物体どおしに働く力を近接相互作用としてとらえるために，電気力線（電場）や磁力線（磁場）を寒天のような弾性体とみなす方法があります。その考え方では，電場・磁場には弾性体と同様な張力と圧力が働いており，電荷をもつ物体が存在する（動く）と，その周辺の「弾性体」がひずみ，そのひずみが遠方まで到達することによって，遠方の電荷をもつ物体が直接的には，ひずんだ「弾性体」から応力を受けると考えます。この応力をマクスウェルの応力と言います。

１．マクスウェルの応力

［１］　誘電性と磁性を合わせ持つ物体が，電場E (r ,t)，磁場(磁束密度B(r ,t))におかれたときに働く力についての一般論を考えます。この物体(＝荷電粒子の集合)には，

(１)　真電荷密度：              ρ ＝ ρ(r ,t)

が存在し，また，

(２)　真電流密度：                 j  ＝ j (r ,t)

が流れ，物体の持つ分極[#]をP ，磁化[#]をM とします。

真電荷，真電流の他には，

(３)　分極電荷密度 [#] ：　　 ρ_P ＝− ｄｉｖ P  

(４)　磁荷の電流密度 [#] ：　j M ＝rot	M
	μ0

(５)　分極電流密度 [#] ：  　 j P ＝	∂P
	∂t

も存在することができます。　したがって，この物体にはたらくローレンツ力[#]は，

F　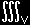＝		｛ (ρ＋ρP)E ＋( j ＋ j M ＋ j P )× B ｝dV

＝

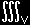(ρ−divP )E ＋

j ＋rot

M

＋

∂P

×B

dV

μ0

∂t

↓

ｄｉｖ(ε0E ＋P ) ＝ ρ[#] と rot H ＝ rot B −M  ＝ j＋ ∂ε0E  ＋ ∂P   [#] を用いて， μ0 ∂t ∂t

＝

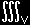div (ε0E )E ＋

rot

B

−

∂ε0E

×B

dV

μ0

∂t

↓	∂(ε0E × B )  ＝ ∂ε0E ×B ＋ε0E × ∂B ∂t ∂t ∂t

＝−

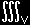∂(ε0E × B )

dV ＋

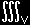ε0E ×

∂B

dV ＋

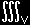div (ε0E )E ＋

rot

B

×B

dV

∂t

∂t

μ0

↓ファラデーの法則　rotE＋∂B/∂t ＝ 0 [#]　とdivB ＝0 [#] に注意して 0 となる項を最後に一つ付け加えて，B→μ₀H として，

＝−

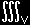∂ε0μ0(E ×H )

dV

＋

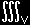ε0rotE ×E ＋ε0 (div E )E

dV ＋

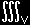μ0 rotH ×H ＋μ0(div H )H

dV

∂t

第１項

第２項

第３項

［２］　第１項　は後ほど述べるように，ε₀μ₀(E ×H )＝(E ×H )/c²を電磁場の持つ運動量密度とみなすことができ，P_t　≡E ×H をポインティングベクトルといいます。　

［３］　第２項 について，x 成分の計算をさらに進めると，(　E ＝ ( E_x，E_y，E_z ) とします。　)

x方向：　f(E)x ＝ε0

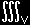∂Ex

−

∂Ez

Ez−

∂Ey

−

∂Ex

Ey ＋

∂Ex

Ex＋

∂Ey

Ex＋

∂Ez

Ex

dV

∂z

∂x

∂x

∂y

∂x

∂y

∂z

↓　少し工夫して　

＝ε0

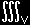2 ・

∂Ex

Ex＋

∂Ey

Ex＋

∂Ez

Ex＋

∂Ex

Ey＋

∂Ex

Ez−

∂Ex

Ex−

∂Ey

Ey−

∂Ez

Ez

dV

∂x

∂y

∂z

∂y

∂z

∂x

∂x

∂ｘ

＝ε0

∂

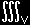Ex2＋

∂

(ExEy)＋

∂

(ExEz)−

1

∂

(Ex2＋Ey2＋Ez2)

dV

∂x

∂y

∂z

2

∂ｘ

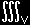＝			div			ε0ExEx −	ε0(E ･E )	， ε0ExEy， ε0ExEz		dV
							2

↑　もちろん，最後のdiv(*，*，*)の(*，*，*)はベクトル成分を意味するつもりの括弧です。

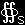＝			ε0ExEx−	ε0(E ･E )	，ε0 ExEy， ε0ExEz		・n dS　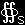＝		TEx ・dS
				2

最後はガウスの定理 [#] を使いました。　

ベクトルT _x の物理的な意味は最後の面積分で表した式から，
物体の表面の単位面積あたりに働く x方向に働く力を，

TEx ≡		ε0ExEx−	ε0(E ･E )	，ε0 ExEy， ε0ExEz
			2

　　　＝( x 軸に垂直な面を通して働く力， y 軸に垂直な面を通して働く力， z軸に垂直な面を通して働く力，)

に分解して表していたものとみなすことができます。このベクトルT _x と面の単位法線ベクトル n との内積：T _x ・n がこの微小面積に働く力の x成分 f_x です。

［４］　同様にy，z成分は，

y方向：　f(E)y 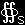＝			ε0EyEx，ε0EyEy−	ε0(E ･E )	，ε0EyEz		・n dS	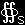＝		TEy ・dS
				2

z方向：　f(E)z 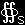＝			ε0EzEx，ε0EzEy，ε0EzEz −	ε0(E ･E )		・n dS	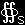＝		TEz ・dS
				2

［５］　第３項 の磁場に関する項も数学的な形式が第２項と全く同じなので，同様な計算のあとに，第２項の結果において，E → H，ε₀ → μ₀ と置き換えただけの式が得られ，上に対応するベクトルもT^E_x ⇒T^H_x と書くことにします。これら第２項，３項の部分の結果だけをまとめて行列(テンソル)を用いて書けば次のようになります。

マクスウェルの応力 n に垂直な単位面積に働く力 f は， Tn ＝ TEx ＋THx  n TEy ＋THy TEz ＋THz ＝ ε0ExEx − ε0E 2 ＋μ0HxHx− μ0H2 2 2 ε0ExEy＋μ0HxHy ε0ExEz＋μ0HxHz n1 　 ε0EyEx＋μ0HyHx ε0EyEy− ε0E 2 ＋μ0HyHy− μ0H2 2 2 ε0EyEz＋μ0HyHz n2 ε0EzEx＋μ0HzHx ε0EzEy＋μ0HzHy ε0EzEz − ε0E 2 ＋μ0HzHz− μ0H2 2 2 n3                   この行列 T はマクスウェルの応力と呼ばれる２階テンソル[#] であって，成分では， Tjk ＝ ε0EjEk− ε0E 2 δjk＋μ0HjHk− μ0H2 δjk　　　　　［ 応力テンソル ］ 2 2 と一行で書くことができます。　　i，j ＝x，y，z

これらの用語･記号を用いると，物体に働く電磁気学的な力は，ε₀μ₀＝1/c²として，

運動量つり合いの式 F ＝ − ∂ (E ×H ) dV  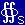＋  T・n dS ∂t c2

と書くことができます。

［６］　E-B対応ならば最後の結果は次のとおりとなります。

マクスウェルの応力 n に垂直な単位面積に働く力 f は， Tn ＝ T x  n T y T z ＝ ε0ExEx − ε0(E ･E ) ＋ BxBx − (B ･B ) 2 μ0 2μ0 ε0ExEy＋ BxBy μ0 ε0ExEz＋ BxBz μ0 n1 　 ε0EyEx＋ ByBx μ0 ε0EyEy− ε0(E ･E ) ＋ ByBy − (B ･B ) 2 μ0 2μ0 ε0EyEz＋ ByBz μ0 n2 ε0EzEx＋ BzBx μ0 ε0EzEy＋ BzBy μ0 ε0EzEz − ε0(E ･E ) ＋ BzBz − (B ･B ) 2 μ0 2μ0 n3                   この行列　T　はマクスウェルの応力と呼ばれ，２階テンソル[#] であって，成分では， Tjk ＝ ε0EjEk− ε0 δjk(E ･E ) ＋ 1 BjBk− 1 δjk(B ･B )　　　　　　　［ 応力テンソル ］ 2 μ0 2μ0 と一行でまとめて書くこともできます。

これらの用語･記号を用いると，はじめに考えた物体に働く力は，

F 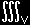＝ − ∂(ε0E × B ) dV  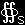＋  T・n dS ∂t

と書くことができます。

［目次へ］