
| 9 ガロアの基本定理 |  |
||
| f-denshi.com 最終更新日: 21/08/17 | |||
| [目次へ] | |||
| サイト検索 | |||
ガロア拡大 K/F が与えられていて,対応するガロア群 G(K/F) が求められている場合を考えます。F上の多項式 f(x) の分解体が K であり,f(x) の根をα1,・・・,αn とします。
| 定理 ガロアの基本定理 1 (1) 体 F のガロア拡大 K/F [#] に中間体 M が存在すれば,ガロア群 G(K/F) [#] には M に 1対1に対応する部分群 HMが存在して, HM=G(K/M)(2) ガロア群 G(K/F) に部分群 H が存在すれば,ガロア拡大 K/F には H に1対1に対応する中間体 MHが存在して, MH={ α∈K|σ(α)=α, ∀σ∈H } |
この様子はまとめて下図のように表されますが,これらの対応↓↑はガロア対応と呼ばれます。
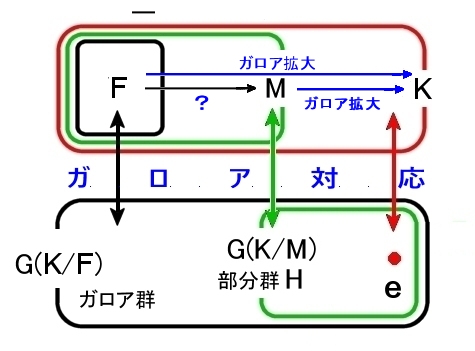
[1]
(1)の証明
(1) ガロア拡大 K/F に中間体 M が存在するとき,K は「Mのガロア拡大」でもあるから,( F(α1,・・・,αn)=M(α1,・・・,αn)=L に注意すると,前ページ定理 [#] の「F上の多項式〜」を「M上の多項式〜」と読み替えてその後の議論を繰り返せば,K/F
がガロア拡大であれば,K/M もガロア拡大であることはすぐに分かる。一方,拡大
M/F がいつもガロア拡大になっているとは限らない[#].。そのことについては後で,「ガロアの基本定理2」で議論する。)
M のすべての元を動かさない 「M上のK自己同型写像全体」 はガロア群 G(K/M) をつくり,その位数は拡大次数 [ K:M ] に等しい[#]。
(2) また,G(K/M)の元はすべて, F (⊂M) の元も動かさず,「F上のK自己同型写像」でもあるから G(K/M) ⊂ G(K/F) である。
(3) したがって,この定理 1ー(1) の部分群 HM には,このガロア群 G(K/M) を一意的に対応させることができる。
[2] (2)の証明。
(1) ガロア拡大 K/F に対応するガロア群 G(K/F) に部分群 H が存在するならば,H のすべての元(K自己同型写像)によって,不変な K の元全体は,「K の部分体 M 」 となり,K ⊃ M ⊃ F を満たす。
α,β∈M ⇒ σ(α+β)=σ(α)+σ(β)=α+β∈M;σ(αβ)=σ(α)σ(β)=αβ∈M
(2) 部分群 H を H={σ1= e,σ2,・・・,σm } とする。
(3) K/M はガロア拡大なので,K=M(θ) となるθを一つ選ぶことができ [#],このθを用いたM上のm次多項式,
g(x)=(x−σ1(θ))(x−σ2(θ))・・・(x−σm(θ)) ←次数 m
を考えると,g(x)の係数はσk(θ)=θ'k (k=1,2,…,m) の対称式なので,部分群 H の元を多項式 g(x) に作用させたとき,g(x) は M上の多項式全体 M[x] からはみ出さない。σ(g(x))∈M(x)。
(4) M上のθの最小多項式φ(x) の次数は [M(θ):M]=[K:M] であるが,φ(x) は g(x) を割り切る。すなわち,[K:M] ≦ m である。
(5) 一方,K は M のガロア拡大であり,対応するガロア群 G(K/M) は M の元を動かさない K自己同型写像をすべて含んでいるので,H⊆G(K/M) である。
すなわち,m=|H| ≦ |G(K/M)|=[K:M] である。
(6) これら2つの不等式から,|H|=|G(K/M)| が分かるが,どちらも G(K/F)
の部分群だから,H=G(K/M) である。(終)
[3]
例 体の拡大: Q ⇒ Q(√2,i ) を考える。
まず, Q(√2,i )=Q(θ) となるθとして。 ←単純拡大体
θ=√2+i
を選び出す。実際,これでうまくいくことは次のように示される。
√2+i =θ∈ Q(√2,i ) は自明。逆は,
θ2=2i √2+1 (1)
θ3=5i−2√2
i =(θ3+2θ)/7
√2=(5θ−θ3)/7
i √2=(θ2−1)/2・・・ [*]
と計算してみれば,√2,i , i√2 ∈ Q(θ) と分かる。よって,Q(√2,i )=Q(θ) が確かめられた。
θの最小多項式は (1)式,(2i √2)2=(θ2−1)2 を利用して,
φ(x)=(x2−1)2+8 = x4−2x2+9
これはあくまで候補にすぎないが,アイゼンシュタインの判定基準[#]から Q上の既約多項式であることが確かめられる。
Q(θ)上のφ(x)の因数分解は,θの複素共役を θ*=√2−i として,
φ(x)=(x−θ)(x+θ)(x−θ*)(x+θ*) ( = x4−(θ2+θ*2)x2+θ2θ*2 )
で与えられ,Q(θ) はφ(x) の分解体 [#] である。共役根θk は,
θ1=θ, θ2=−θ, θ3=θ*, θ4=−θ* ・・・ [**]
自己同型写像σk ( k=1,2,3,4 ) は,θを θ1,θ2,θ3,θ4 にそれぞれ対応させることで [*] と[**]より一意的に決められる。
σ1は,σ1(θ)=θ1=θと対応させて,これは恒等写像なので,
σ1(θ2)=θ2
σ1(θ3)=θ3
σ1(θ4)=θ4
σ2 は,
σ2(θ)=θ2=−θ
と対応させると,残りの写像は,
σ2(i ) =σ2((θ3+2θ)/7) =(−θ3−2θ)/7=−i
σ2(√2) =σ2((5θ−θ3)/7)=(−5θ+θ3)/7 =−√2
のように計算して,これを用いれば,
σ2(θ2)=θ =θ1
σ2(θ3)=−θ*=θ4
σ2(θ4)=θ* =θ3
と一意的に定まります。
同様に,σ3(θ)=θ3 ,σ4(θ)=θ4 と定めて自己同型写像の働きを調べると,下記のとおりにまとめられます。
| α = | θ1 | θ2 | θ3 | θ4 | √2 | i | i √2 |
| e =σ1(α)= | θ1 | θ2 | θ3 | θ4 | √2 | i | i √2 |
| σ2(α)= | θ2 | θ1 | θ4 | θ3 | −√2 | -i | i √2 |
| σ3(α)= | θ3 | θ4 | θ1 | θ2 | √2 | -i | -i √2 |
| σ4(α)= | θ4 | θ3 | θ2 | θ1 | −√2 | i | -i √2 |
これより,自己同型写像σk ( k=1,2,3,4 ) は共役根を上表のように入れ換えるガロア群であることが分かります。
また,i,√2,i√2 を不変にする3つの部分群{ σ1,σ3},{ σ1,σ4} ,{ σ1,σ2} の存在が分かるが,これらに対応する3つの中間体が存在し,以下のように対応させられます。
{σ1,σ2,σ3,σ4} ⊃ { σ1,σ3} ⊃ { σ1} Q ⊂ Q(√2) ⊂ Q(θ)
{σ1,σ2,σ3,σ4} ⊃ { σ1,σ4} ⊃ { σ1} Q ⊂ Q(i ) ⊂ Q(θ)
{σ1,σ2,σ3,σ4} ⊃ { σ1,σ2} ⊃ { σ1} Q ⊂ Q(i √2) ⊂ Q(θ)
| 定理 ガロアの基本定理2 (1) 体F のガロア拡大 K/F に中間体 M が存在するとき,M が F のガロア拡大であれば,G(K/M) は G(K/F) の正規部分群であり, G(M/F) ≡ G(K/F)/G(K/M) [ 同型 ]が成り立つ。 逆に, (2) H を ガロア群 G(K/F) の正規部分群とすると,H に対応する K の中間体 M は F のガロア拡大であって,H=G(K/M) が成り立つ。
|
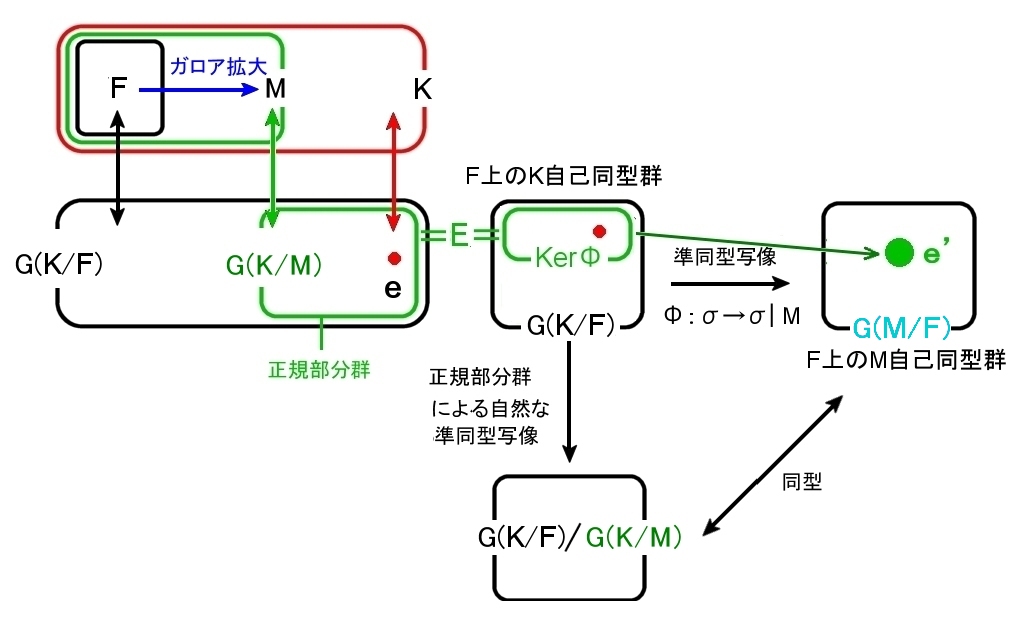
基本定理1のガロア対応においては,「K/F がガロア拡大であれば,拡大 K/M もガロア拡大 (ほぼ自明)である。」と述べていましたが,拡大 M/F については何も述べていませんでした。
この基本定理2では,「拡大 M/F がガロア拡大となる必要十分条件は,G(K/M) が G(K/F) の正規部分群であること」 を主張しています。
言い換えると,ガロア拡大を F ⇒ M ⇒ K と繰り返して,ガロア拡大 F ⇒
K が得られるときのガロア群と部分群の関係を示していることになります。
[6] 証明
体K を ( F を部分体として含む ) M に制限して考えることにすると,・・・
(1) G(K/M) の元は M を動かさない元(自己同型写像)であるから,(Mに属さないKの元の挙動を無視すれば,) ,G(K/M)のすべての元は恒等写像であり,G(K/M)を単位元 e' ∈ G(M/F) に写す準同型写像,
Φ: G(K/F) ⇒ G(M/F) ← F上のM自己同型写像 (G(K/M)=KerΦ)
を考えることができる。(確認は難しくない)
(2) 準同型定理 [#] ,[#] によれば,群の準同型写像Φの核G(K/M)は正規部分群であり,自然な準同型写像の像: G(K/F)/G(K/M) とΦの像 G(M/F) は同型である。
この逆は,
(3) G(K/F) の正規部分群 H で動かない K の元全体は, K の部分体 Mとなる。自己同型写像の定義を見よ→[#]
(4) (F上代数的な) 任意の M の元θを,その共役根θ’へ写す自己同型写像σ∈G(K/F) を [#],σ(θ)=θ’とする。
(5) すると,任意のτ∈H について,σ-1τσ∈H であるから,←正規部分群 [#] なので
σ-1τσ(θ)=θ ⇔ τσ(θ)=σ(θ)=θ’ ⇔ τ(θ’)=θ’ ←θ’はτで動かない
(6) これは,θ’∈M を意味する。つまり,θ∈M の共役根θ’は M の中にある。
⇔ M/F は正規拡大であり,ガロア拡大
(7) したがって,H はガロア群であり,その定義からG(M/F)と表すべきものである。
例
[7] 先ほどの例:体の拡大: Q ⇒ Q(√2,i ) について再び考えます。
ガロア群 G(Q(θ)/Q) には3つの部分群がありました [#] が,容易にいずれも正規部分群であることが分かります。その一つ, E3={ e,σ3 } による剰余群の群表を下に示します。
G(Q(θ)/Q)={σ1,σ2,σ3,σ4}≡{ e,(12)(34),(13)(24),(14)(23) }=クラインの4元群に同型
|
⇒ |
|
||||||||||||||||||||||||||||||||||
| ガロア群 G(Q(θ)/Q) G(K/F) |
剰余群 G(Q(θ)/Q)/G(Q(θ)/Q(√2)) ≡G(Q(√2)/Q) G(K/F)/G(K/M)≡G(M/F) |
位数が2の正規部分群は全部で3つ (σ1=e )
{ e,σ3 } ⇒ Q√2)/Q はガロア拡大
{ e,σ4 } ⇒ Q( i )/Q はガロア拡大
{ e,σ2 } ⇒ Q(i √2)/Q はガロア拡大
これら3つの正規部分群は,さらに正規部分群 { e } をもっており,
Q(√2,i )/Q√2) はガロア拡大
Q(√2,i )/Q( i ) はガロア拡大
Q(√2,i )/Q(i √2) はガロア拡大
となります。←これは,「K/M=必ずガロア拡大」 に対応
包含関係から次のように図示できます。
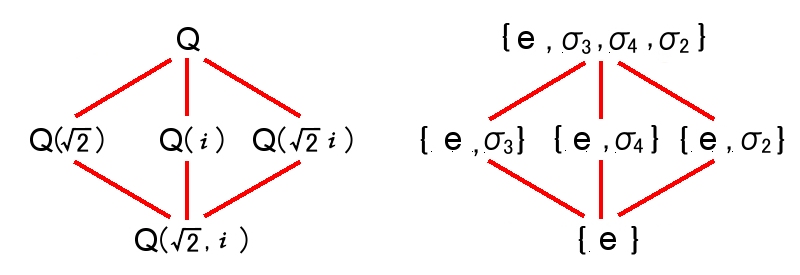 |
| 赤線は上から下へガロア拡大,および,正規部分群であることを示す。 |
[10]
ガロアの基本定理2の証明に用いた図 [#] をこの例に当てはめた図は下のとおりとなります。
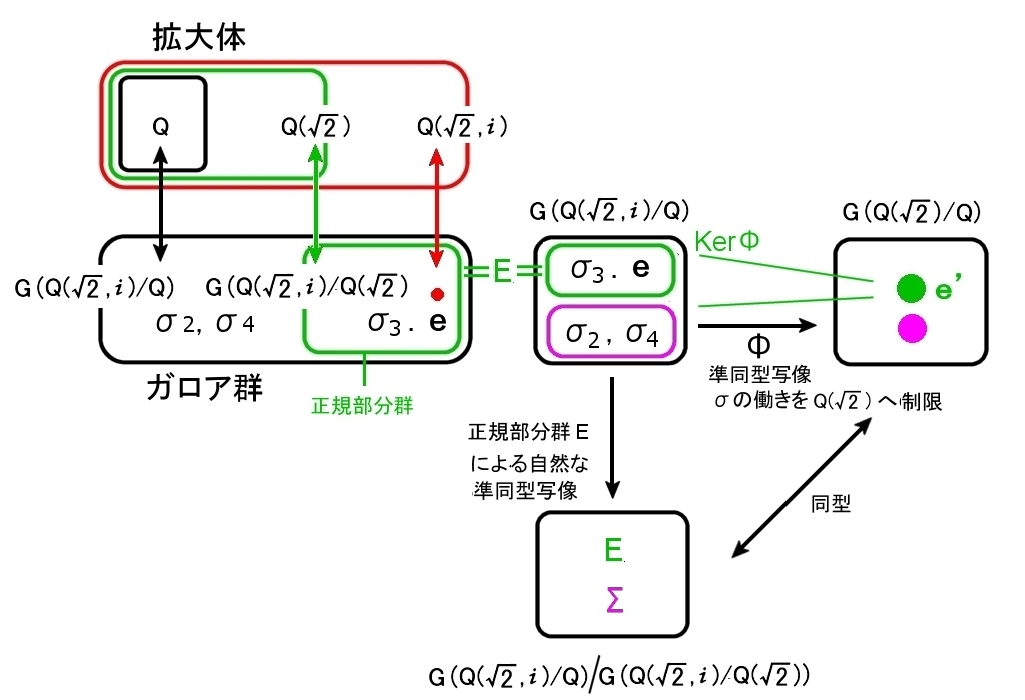
[7]
例 Q から中間体 M への拡大が必ずしもガロア拡大とは限らない場合。
Q上の多項式,
f(x)=x3−2 ∈ Q[x]
の分解体を K とする拡大 K/Q を考えます。
| α= | 2 | ,および,g(x)=x2+x+1 の根の一つを ω=exp(2πi /3) として, |
f(x)=(x−α)(x−ωα)(x−ω2α) ←共役根 α,ωα,ω2α
と因数数分解でき,分解体 K=Q(α,ω) の任意の元は,
1,α,α2,ω,ωα,ωα2 基底
を基底にとって表せます。よって, [ K:Q ]=6と予想できます。(実際これは正しい)
中間体は,Q(α),Q(ω),Q(ωα),Q(ωα2)が考えられます。 ←Q(α2) ⊂Q(α)
中間体 Q(ω) を動かさず,αをαの共役根に動かす自己同型写像は,
σ1(α)=ωα
σ2(α)=ω2α
の2つがあって,
σ12(α)=σ2(α), σ13(α)= e(α)
が確かめられます。
中間体 Q(α) を動かさず,ωをωの共役根ω2に動かす自己同型写像τを
τ=τ1 : τ1(ω)=ω2
とします。さらに,以上これらの同型写像の積も群に含ませるために
τ2=τσ1
τ3=τσ2
も定めます。いくつか計算してみると,
τ2(α)=τ(σ1(α))=τ(ωα)=ω2α
τ2(ωα)=τ(σ1(ωα))=τ(ω2α)=ωα
τ3(ω2α)=τσ2(ω2α))=τ(ωα)=ω2α
[8]
他の元についても f(x),g(x) の根への作用を計算すれば,
下の一覧表・ガロア群 G(K/Q)={ e,σ1,σ2,τ1,τ2,τ3 } の積表が得られます。
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ガロア群の体Kの元へ働き | ガロア群 G(K/Q) の積表 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 剰余群 G(K/Q) / G(K/Q(ω)) ≡ガロア群 G(Q(ω)/Q)の積表 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 剰余類 A= { e,σ1,σ2 } 剰余類 T= {τ1,τ2,τ3 } |
{ e,σ1,σ2 } は G(K/Q) の正規部分群(赤背)で,ガロア群 G(K/Q(ω))
{ A,T } は剰余群 G(K/Q)/G(K/Q(ω)) で,ガロア群 G(Q(ω)/Q) に同型
6=|G(K/Q)|
3=|G(K/Q(ω))| 最小多項式=x3−2
2=|G(Q(ω)/Q)| 最小多項式=x2+x+1
| ガロア群 | 体 | |||
| ω | を動かさない部分群 | { e,σ1,σ2 } | ⇔ | Q(ω) |
| α | を動かさない部分群 | { e,τ1 } | ⇔ | Q(α) |
| ωα | を動かさない部分群 | { e,τ2 } | ⇔ | Q(ωα) |
| ω2α | を動かさない部分群 | { e,τ3 } | ⇔ | Q(ω2α |
| Kの元 | を動かさない部分群 | { e } | ⇔ | Q(α,ω) |
| Qの元 | を動かさない部分群 | G(K/Q} | ⇔ | Q |
[13]
これらの考察から,ガロア群 G(K/Q)の部分群と分解体の部分体を対応付けると,以下のとおりにまとめられます。
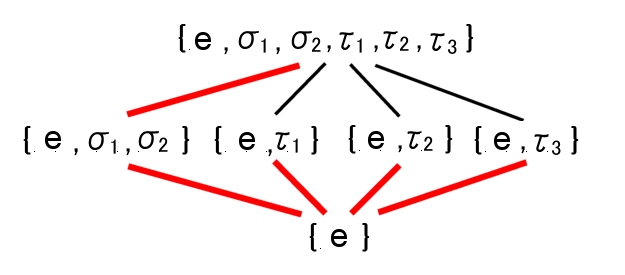 |
| ガロア群と部分群 (赤線: 正規部分群) |
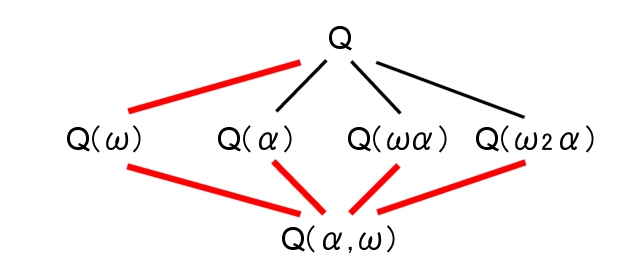 |
| Qの拡大体と中間体 (赤線: ガロア拡大) |
Qからのガロア拡大となっている中間体は Q(ω) だけです。
これ対応する G(K/Q) の正規部分群は,{ e,σ1,σ2 } です。そして,自明でない正規部分群はこれだけです。
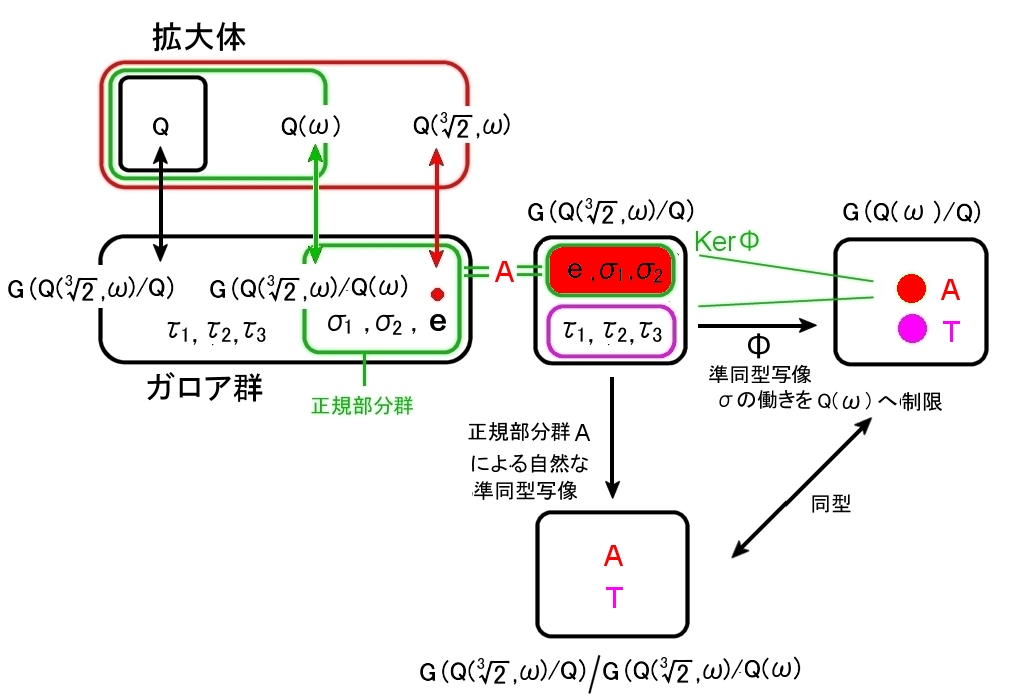
[1] 体 K が与えられていると,K の自己同型写像全体からなる群 Aut K が定まりますが,Aut K が有限部分群 G を持っているという情況で考えます。
| 定理 ガロアの基本定理3 体 K の自己同型写像全体からなる群 Aut K の有限な部分群が G が与えられたとき,G の元(写像)によって不変な K の元全体からなる K の部分体を F とする。 そのとき,拡大 K/F はガロア拡大となっており, G=G(K/F) , [ K:F ]=| G |が成り立つ。 |
[2] 証明
(1) 体 K に属する一つの任意の元αを動かさない群 G の元全体からなる G の部分群を,
Hα={ σ∈G|σ(α)=α } ⊂ G
とする。σs(α)=σt(α) を同値関係とする Hαによる G の左剰余類別 (右でも構わない),
G= σ1Hα∪ σ2Hα∪・・・∪ σmHα
を考える [#]。ここで,σk (=1,2,…,m) ∈G は各同値類の代表元で,同値類の個数を m とした。このとき,
m ≦|G|
(2) すると,α∈K の像,
α1=σ1(α)
α2=σ2(α)
・・・
αm=σm(α)
はすべて異なり, m個で元からなることが分かる。
なお,σ1=e (恒等写像),すなわち,α1=αとする。
(3) このαmを用いて,係数が対称式となる多項式
fα(x)=(x−α1)(x−α2) ・・・ (x−αm) ← αkはすべて異なる
を考えると,これは F 上の多項式 F[x] に属する。 ←(2)は自己同型写像を定め,αkは共役根というワケで,そのすべてからなる対称式はGの元では動かない,つまり,Fの元。
(4) αはF上の代数的な元であって, fα(x) はαの最小多項式 φ(x) で割り切れるので,φ (x)の次数 = [ F(α):F ] [#] は fα(x) の次数 m 以下である。
[ F(α):F ] ≦ m ≦ | G |
ところで,αは任意の K の元であったから,結局,
[ K:F ] ≦ | G | ・・・ [*] [#]
でなければならない。
(7) fα(x) は重根をもたないのでφ(x) も重根をもたず,K は F上分離的 [#] である。
また,F に関するαの共役元はすべて K に属するので,K は F のガロア拡大 [#] である。
(8) したがって,σk∈ G(K/F) であり,G はその部分群である,すなわち, G ⊂ G(K/F) 。そのとき,
|G|≦| G(K/F)|=[ K:F ]
(9) この不等式と [*] から,等式,
| G | = | G(K/F) | = [ K:F ]
が成り立つ。すなわち,
G = G(K/F)
でなければならない。 (終)
[1]
| 定理 ガロア拡大 K/F に対応するガロア群を G(K/F) とするとき, 「K/F が累巡回拡大である」 と 「G(K/F) が可解群 [#] である」ことは同値である。 |
ガロア拡大 K/F に中間体が2個以上入れ子で存在するときを含めて,すべての体の拡大ステップに対するガロアの基本定理2 [#] をひと言で表したものです。
[2] 証明の概略
(1) まず,体 F と体 K の間に中間体がいくつかあり,次のような包含関係と対応するガロア群があるとします。
F=M0 ⊂ M1 ⊂ … ⊂ Mk-1 ⊂ Mk ⊂ … ⊂ Mm=K ガロアの基本定理2では→ F M K G(K/F) ⊃ G(K/M1) ⊃ … ⊃ G(K/Mk-1) ⊃ G(K/Mk) ⊃ … ⊃ e ガロアの基本定理2では→ G(K/F) G(K/M) e
ガロアの基本定理2
ここで,
Mk ⇔ M
Mk-1 ⇔ F
と読み替えれば,剰余群については,
G(M/F) ≡ G(K/F)/G(K/M) ⇒ G(Mk/Mk-1) ≡ G(K/Mk-1)/G(K/Mk)
( k=1,2,・・・,m )
と読み替えることになります。これを踏まえると,
(2) 定理の⇒は,
各 k について G(Mk/Mk-1) が巡回群ならば,それらは可換群であるので,G(K/F)は可解群 [#] となります。
(3) 逆は,次の定理
有限個の元から生成される可換群は,ある巡回群の直積に同型である。
を考慮すると,
各 k について G(Mk/Mk-1) ( k=1,2,…,m ) が正規部分群であり,可換群ならば,それらはすべて巡回群になっています。このとき,ガロアの基本定理2から拡大 Mk/Mk-1 ( k=1,2,…,m ) はすべてガロア拡大となっています。そのとき,全体としての「拡大 K/F は 累巡回拡大である」といいます。
| * | e | σ4 | σ2 | σ3 |
| e | e | σ4 | σ2 | σ3 |
| σ4 | σ4 | e | σ3 | σ2 |
| σ2 | σ2 | σ3 | e | σ4 |
| σ3 | σ3 | σ2 | σ4 | e |
| * | e | σ2 | σ3 | σ4 |
| e | e | σ2 | σ3 | σ4 |
| σ2 | σ2 | e | σ4 | σ3 |
| σ3 | σ3 | σ4 | e | σ2 |
| σ4 | σ4 | σ3 | σ2 | e |