ときわ台学/電磁気学の原理/光の反射と透過(屈折)

	Appendix B4 光の反射と透過(屈折)
f-denshi.com 　［目次へ］　更新日：10/03/27
サイト検索

１．不連続面における電磁場の満たすべき境界条件

［１］　媒体の誘電率や透磁率がある面において不連続に変化する場合で，なおかつ，その不連続面に電荷や電流が存在しないとき，この不連続面における電磁場の境界条件は次のようになります。

（１）電場 E 、磁場 H （面電流存在しないとき）の接線成分は連続　
（２）電気変位 D 、磁束密度Ｂ（面電荷存在しないとき）の法線成分は連続

（１）		E ･dr ＝0

（２）

D ･n dS ＝ 0　

（簡単な説明）

ここでは，xy平面を不連続面として説明します。z＞0 の領域は空気，z＜0 の領域は水というような状況を思い浮かべるとよいでしょう。

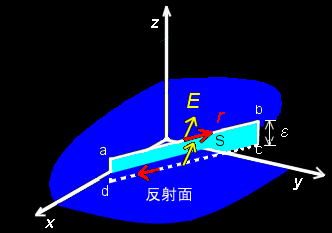
［２］　上図左のような不連続面(xy平面)と交わるz軸と平行な任意の長方形abcdを考えます。このとき，不連続面(付近)に電荷や電流が存在しない ( j＝0 ) ならば，rot E =0， rot H = 0 が成り立ちます。したがって，長方形の内部の面S，その周囲Cのついてストークスの定理を用いれば，

　E ･dr ＝ rotE ･dS ＝0　　　[#]　

および，

　H ･dr ＝ rotH ･dS ＝0　　　[#]　

が成り立ちます。これが，図の辺ab，および，bc→0 の極限で成り立つためには，（１）の主張が任意の不連続面上の点で成り立つことが必要です。

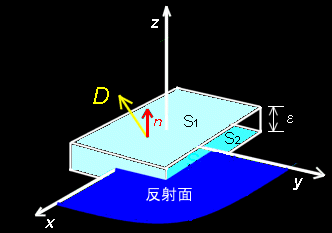
［３］　一方，div D ＝div B ＝0　でもあるので，今度は，上図右のような直方体にガウスの定理[#]を用いて，

D ･n dS＝ divD dV ＝ 0　　　[#]

および，

B ･n dS＝ divB dV ＝ 0　　　[#]

が得られます。これが，直方体の幅ε上下の面積S→0 の極限で成り立つためには，（２）の主張が任意の不連続面上の点で成り立たなければなりません。

２．不連続面における電磁波(平面波)の反射と透過(屈折)

［１］　均質な媒体中では，電磁波は直線的に進行します。しかし，媒体が不均一であったり，不連的な変化がある場所では，電磁波は進行方向を変えます。これは歪んだガラス越しの景色が歪んで見えたり，水面の底が実際より浮き上がって見えたり，鏡に自分の顔を映したりと日常的に経験していることです。ここではそれらがどのような原理に基づいているのか定量的に考察してみます。

まず，結果をまとめておきます。

透明な媒体の反射率：　n₁ （媒体1）　⇒　n₂ （媒体2）

振幅反射率：　r_s ＝	E₀^(r)	＝－	sin (θ_i－θ_t)

	E₀⁽ⁱ⁾		sin (θ_i＋θ_t)
フレネルの第1方程式

r_p ＝	E₀^(r)	＝	tan (θ_i－θ_t)

	E₀⁽ⁱ⁾		tan (θ_i＋θ_t)
フレネルの第2方程式

パワー反射率：　R_s ＝	｜E₀^(r)｜²	＝	sin²(θ_i－θ_t)

	｜E₀⁽ⁱ⁾｜²		sin² (θ_i＋θ_t)

R_p ＝	｜E₀^(r)｜²	＝	tan²(θ_i－θ_t)

	｜E₀⁽ⁱ⁾｜²		tan²(θ_i＋θ_t)

パワー透過率： T_s ＝　

4n₁cosθ_i
4n₁cosθ_i		n₂²-n₁²sin²θ_i

	n₁cosθ_i＋				²
			n₂²-n₁²sin²θ_i

T_p ＝　

4n₁cosθ_i
4n₁cosθ_i		n₂²-n₁²sin²θ_i

	n₂cosθ_i＋（n₁/n₂）				²
			n₂²-n₁²sin²θ_i

垂直入射　　

振幅反射率：　r_⊥ ＝	E₀^(r)	＝	n₁－n₂	、振幅透過率：　t_⊥ ＝	E₀^(r)	＝	2n₁

	E₀⁽ⁱ⁾		n₁＋n₂		E₀⁽ⁱ⁾		n₁＋n₂

パワー反射率：　R_⊥ ＝	｜E₀^(r)｜²	＝	（n₁－n₂）²	、　パワー透過率：　T_⊥ ＝	｜E₀^(t)｜²	＝	4n₁n₂

	｜E₀⁽ⁱ⁾｜²		（n₁＋n₂）²		｜E₀⁽ⁱ⁾｜²		（n₁＋n₂）²

吸収性媒体の反射率：　n　⇒　n＝n ＋iκ　（ ε_r＝ε₁＋iε₂ ）と置き換え

垂直入射
振幅反射率：　r ＝｜r｜e^iθ＝
　　

E₀^(r)

＝

n₁－n₂

n₁＝1
n₂＝n +iκ
のとき
　⇒

＝


1－		ε_r

＝

1－n－iκ

E₀⁽ⁱ⁾

n₁＋n₂


1＋		ε_r

1＋n＋iκ

垂直入射パワー反射率：　R ＝ r ･r^* ＝	（1－n）²＋κ²

	（1＋n）²＋κ²

n　＝

1－R

、　 κ ＝


2		R	sinθ


1＋R＋2		R	cosθ


1＋R＋2		R	cosθ

（注意）　　複素屈折率のκを正に定義しています。

［２］　上の説明をしておきましょう。

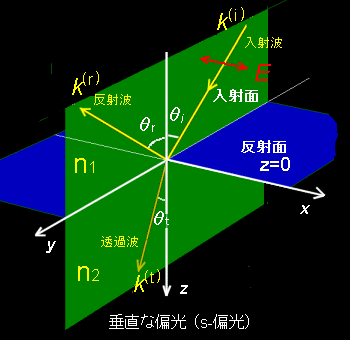
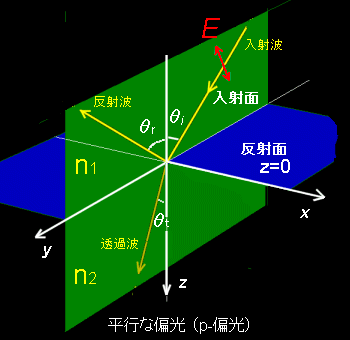
媒体は反射面と呼ばれるxy平面を境界として不連続であり，その屈折率は，z＜0の領域(媒体１)ではn₁，z＞0の領域(媒体２)ではn₂とします。また，それぞれの領域内で各媒体は均一であるとします。ここで，座標軸を，+zの方向が下方に向くように図示していることに注意してください。電磁波は，媒体１の中を入射面と呼ばれるyz平面内を進行し，反射面内にある原点において，一部は反射し，媒体１の中を進行し続けますが，残りは反射面を透過し，媒体２の中を進行するとし，吸収は起こらないとします。このとき，z方向と入射波の進行方向となす角度を入射角，-z方向と反射波の進行方向となす角度を反射角と言います。一方，透過波のある側を向く反射面の法線ベクトル(+z方向)が透過波の進行方向となす角度を屈折角と言います。

電磁波の進行方向は波数ベクトルkで表されます[#]が，これと垂直な方向に電場E，磁場Hが振動しており，

k ×E ＝μ₀ωH　　　　　･･･(1)

の関係を満たしています。反射-屈折の問題を考える上では，この電場の振動方向に着目し，入射面に対して常に垂直なs-偏光と，平行なp-偏光とに分けて考えると便利です。電磁波はこの２つ偏光波の重ね合わせ(線形結合)で表せますからこの2つを調べておけば十分です。

［３］　ｓ偏光の電磁波を平面波，

E （r，t ）＝E₀ exp [ i ( k ･r － ωt ) ] ，　r ＝(x,y,z)　　　　　[一般的な場合]

として取り扱うこととしましょう。すると，入射波，反射波，透過波を表す各平面波は次のようなベクトル成分で表せます。

　E⁽ⁱ⁾ ＝ (E₀⁽ⁱ⁾ exp {i (k_y⁽ⁱ⁾y＋k_z⁽ⁱ⁾z－ωt)}, 0, 0 )，k⁽ⁱ⁾ ＝ ( 0,k_y⁽ⁱ⁾,k_z⁽ⁱ⁾)　　[入射波]
　E^(r) ＝ (E₀^(r) exp {i (k_y^(r)y＋k_z^(r)z－ωt)}, 0, 0 )，k^(r) ＝ ( 0,k_y^(r),k_z^(r))　[反射波]
　E^(t) ＝ (E₀^(t) exp {i (k_y^(t)y＋k_z^(t)z－ωt)}, 0, 0 )，k ^(t) ＝ ( 0,k_y^(t),k_z^(t))　[透過(屈折)波]

ここで，誘電体中のk　については，|k|²c₀²＝n²ω²の関係が成り立つので[#]，

|k⁽ⁱ⁾|²c₀²＝n₁²ω²，　|k^(r)|²c₀²＝n₁²ω²，　|k^(t)|²c₀²＝n₂²ω²　　　・・・(2)

これより，

|k⁽ⁱ⁾|² ＝ |k^(r)|² ＝ |k^(t)|² ＝ ω²

n₁² n₁² n₂² c₀²

この一つ目の”＝”より，

|k⁽ⁱ⁾|²＝|k^(r)|² 　　　⇔　　　(k_y⁽ⁱ⁾)²＋(k_z⁽ⁱ⁾)² ＝ (k_y^(r))²＋(k_z^(r))²　　　　　・・・(3)

平面　z＝0　上の接線，x軸方向における電場の連続性（１）から，媒体１側にある入射波＋反射波のx成分と媒体２側にある透過波のx成分が等しくなければならないとして，

　E₀⁽ⁱ⁾exp {i (k_y⁽ⁱ⁾y－ωt)} ＋ E₀^(r)exp {i (k_y^(r)y－ωt)} ＝ E₀^(t)exp {i (k_y^(t)y－ωt)}　　･･･　[*]

特に t＝0 においても，任意のｙについてこの式が成り立つ必要があるので，

k_y⁽ⁱ⁾＝k_y^(r)＝k_y^(t)

であることが必要条件として要求されます。したがって，(3)からz成分について，

(k_z⁽ⁱ⁾)²＝(k_z^(r))²

も成り立つ必要があります。さらに，入射角と反射角について考えているので，

k_z⁽ⁱ⁾＝－k_z^(r)

のように符号を取ります。したがって入射角と反射角は，

θ_i ＝θ_r

が成立します。

［４］　一方，入射角θ_i，屈折角θ_tと波数ベクトルとの間には(2)より，

k_z⁽ⁱ⁾ ＝|k⁽ⁱ⁾|cosθ_i＝ n₁ω cosθ_i

c₀

k_z^(t) ＝|k^(t)|cosθ_t＝ n₂ω cosθ_t

c₀

一方，

k_y⁽ⁱ⁾ ＝sinθ_i　， k_y^(t) ＝sinθ_t　

|k⁽ⁱ⁾| |k^(t)|

したがって，k_y⁽ⁱ⁾＝k_y^(t)であることと (2) を思い出せば，

sinθ_t ＝ |k⁽ⁱ⁾| ＝ n₁

sinθ_i |k^(t)| n₂

これは，スネルの式と呼ばれます。

n₁sinθ_i＝n₂sinθ_t　　　[スネルの式]

結局，以上の波数ベクトルに課される条件の下で[*]は，

E₀⁽ⁱ⁾＋E₀^(r)＝E₀^(t)　　　　　･･･　[**]

となります。

［５］　一方，(1)を用いて，入射波の磁場Hは，

H⁽ⁱ⁾＝	1	k⁽ⁱ⁾×E⁽ⁱ⁾

	μω

＝	1	0， k_z⁽ⁱ⁾E₀⁽ⁱ⁾ exp {i (k_y⁽ⁱ⁾y－ωt)}， -k_y⁽ⁱ⁾E₀⁽ⁱ⁾ exp {i (k_y⁽ⁱ⁾y－ωt)}	←ベクトル

	μω

同様に，

H^(r)＝	1	0，k_z^(r)E₀^(r) exp {i (k_y^(r)y－ωt)}， -k_y^(r)E₀^(r) exp {i (k_y^(r)y－ωt)}

	μω

H^(t)＝	1	0，k_z^(t)E₀^(t) exp {i (k_y^(t)y－ωt)}， -k_y^(t)E₀^(t) exp {i (k_y^(t)y－ωt)}

	μω

と表されます。このうち，z＝0平面の磁場Hの接線成分，特にy成分が連続であるためには

　k_z⁽ⁱ⁾E₀⁽ⁱ⁾ exp {i (k_y⁽ⁱ⁾y－ωt)}＋k_z^(r)E₀^(r) exp {i (k_y^(r)y－ωt)}＝k_z^(t)E₀^(t) exp {i (k_y^(t)y－ωt)}

　　　　　　　　　　　　　↓↑

k_z⁽ⁱ⁾E₀⁽ⁱ⁾ ＋k_z^(r)E₀^(r) ＝k_z^(t)E₀^(t)　　･･･　[***]

　[**]と　[***]とを連立して解き，k_z⁽ⁱ⁾＝－k_z^(r)であることを用いれば，

E₀^(r) ＝　 k_z⁽ⁱ⁾－k_z^(t) 　E₀⁽ⁱ⁾

k_z⁽ⁱ⁾＋k_z^(t)

E₀^(t) ＝　 2k_z⁽ⁱ⁾ 　E₀⁽ⁱ⁾

k_z⁽ⁱ⁾＋k_z^(t)

のように反射波，屈折波の振幅を入射波の振幅で表すことができます。ただし，波数ベクトル成分に関しては，

k x成分 y成分 z成分

入射波　k⁽ⁱ⁾ 0

n₁ω sinθ_i

c₀

n₁ω cosθ_i

c₀

反射波　k^(r) 0

n₁ω sinθ_r

c₀

－ n₁ω cosθ_r

c₀

透過波　k^(t) 0

n₂ω sinθ_t

c₀

n₂ω cosθ_t

c₀

これらとスネルの式を用いて計算を進めると，次のように定義される振幅反射率は，

E₀^(r) ＝ n₁cosθ_i－n₂cosθ_t

E₀⁽ⁱ⁾ n₁cosθ_i＋n₂cosθ_t

　　　　　＝ sinθ_tcosθ_i－sinθ_icosθ_t

sinθ_tcosθ_i＋sinθ_icosθ_t

　　　　　＝－ sin(θ_i－θ_t) 　　フレネルの第１方程式

sin(θ_i＋θ_t)

入射角と屈折各で表されます。この結果はフレネルの第１方程式と呼ばれます。同様に振幅透過率は，

E₀^(t) ＝ 2k_z⁽ⁱ⁾ ＝ 2n₁cosθ_i

E₀⁽ⁱ⁾ k_z⁽ⁱ⁾＋k_z^(t) n₁cosθ_i＋n₂cosθ_t

　　　　　＝ 2cosθ_isinθ_t

sin(θ_i＋θ_t)

［６］　特に垂直入射θ_i＝0 のとき(θ_t＝0) は，１行目の式に戻って，cosθ_i＝cosθ_t＝1 とすれば，垂直入射反射率として，

r_⊥ ＝ n₁－n₂

n₁＋n₂

t_⊥ ＝ 2n₁

n₁＋n₂

が得られます。また，垂直パワー反射率，および，垂直パワー透過率は，

R_⊥ ＝ E₀^(r) 2 ＝ (n₁－n₂)²

E₀⁽ⁱ⁾ (n₁＋n₂)²

T_⊥ ＝1－R_⊥

［７］　金属のような吸収性の物質の場合は，n₁ ⇒ １（真空）　，　n₂ ⇒ n ＋iκと置き換えればよい。

振幅反射率：　r_⊥ ＝	n₁－n₂	⇒	1－(n ＋iκ)

	n₁＋n₂		1＋(n ＋iκ)

金属反射についての説明は省略。
p-偏光についての計算は省略。
偏向角（ブリュースター角)，全反射についての説明は省略。

［目次へ］

\|k⁽ⁱ⁾\|²	＝	\|k^(r)\|²	＝	\|k^(t)\|²	＝	ω²

n₁²		n₁²		n₂²		c₀²

E₀^(r)	＝	n₁cosθ_i－n₂cosθ_t

E₀⁽ⁱ⁾		n₁cosθ_i＋n₂cosθ_t

＝					sinθ_tcosθ_i－sinθ_icosθ_t

					sinθ_tcosθ_i＋sinθ_icosθ_t

＝－	sin(θ_i－θ_t)	フレネルの第１方程式

	sin(θ_i＋θ_t)

E₀^(t)	＝	2k_z⁽ⁱ⁾	＝	2n₁cosθ_i

E₀⁽ⁱ⁾		k_z⁽ⁱ⁾＋k_z^(t)		n₁cosθ_i＋n₂cosθ_t

R_⊥ ＝	E₀^(r)	2	＝	(n₁－n₂)²

	E₀⁽ⁱ⁾			(n₁＋n₂)²